leetcode每日一题34

89.格雷编码

观察一下n不同时的格雷编码有什么特点
n=1 [0,1]
n=2 [0,1,3,2]
n=3 [0,1,3,2,6,7,5,4]
……
可以看到n=k时，编码数量是n=k-1的数量的一倍
同时n=k编码的前半部分和n=k-1一模一样
n=k编码的最后一位是2^k-1
后半部分的编码是其对应的前半部分的对称的位置的数字+2^k-1
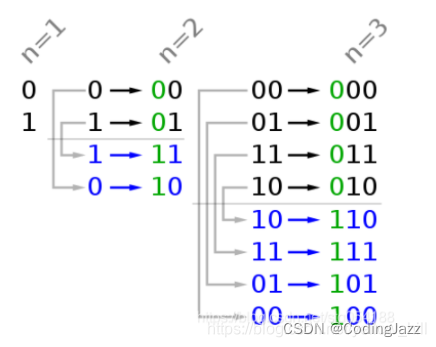在这里插入图片描述如图可以看出原理，为了增加长度后，使得隔着中轴线相邻的第2^k-1位和第2^k-1+1位差一位，那么就要在新增加的位上由0变1(因为前半部分出现过在原有的位上是1的编码了）
也就是数字上增加了2^k-1
至于其他的位，因为按照前面的编码放置1的顺序是唯一的，所以只要在最高位都填1，然后对称着顺序来就好了

因此代码为

class Solution {
public:
    vector&lt;int&gt; grayCode(int n) {
        vector&lt;int&gt; gray;
        gray.push_back(0);
        gray.push_back(1);
        if(n==1)
            return gray;
        for(int i=2;i<=n;i++)
        {
            for(int j=pow(2,i-1)-1;j>=0;j--)
            {
                gray.push_back(gray[j]+pow(2,i-1));
            }
        }
        return gray;
    }
};

格雷编码有相当多的生成方法
还有一种，比如说G(i)=(i ^ (i >> 1))也就是G(i)=i^(i/2)
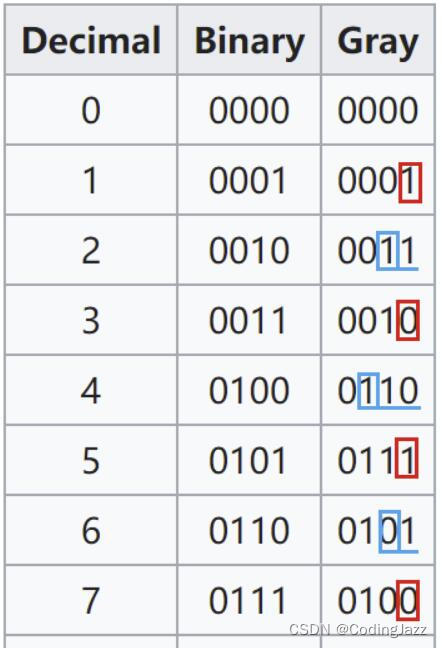在这里插入图片描述从这个图可以看出，如果二进制码字的第 i 位和 i+1 位（从右边开始数）相同，则对应的格雷码的第i位为0，否则为1（当i+1=n时，二进制码字的第n位被认为是0，即第n-1位不变）

class Solution {
public:
    vector<int> grayCode(int n) {
        vector<int> gray;
        for(int i=0;i<pow(2,n);i++)
            gray.push_back(i^i>>1);
        return gray;
    }
};