左孩子右兄弟(Java详解)

目录

一、题目描述

二、题解

一、题目描述

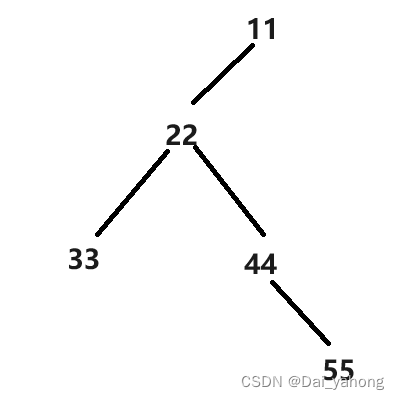
对于一棵多叉树，我们可以通过“左孩子右兄弟” 表示法，将其转化成一棵二叉树。
如果我们认为每个结点的子结点是无序的，那么得到的二叉树可能不唯一。
换句话说，每个结点可以选任意子结点作为左孩子，并按任意顺序连接右兄弟。
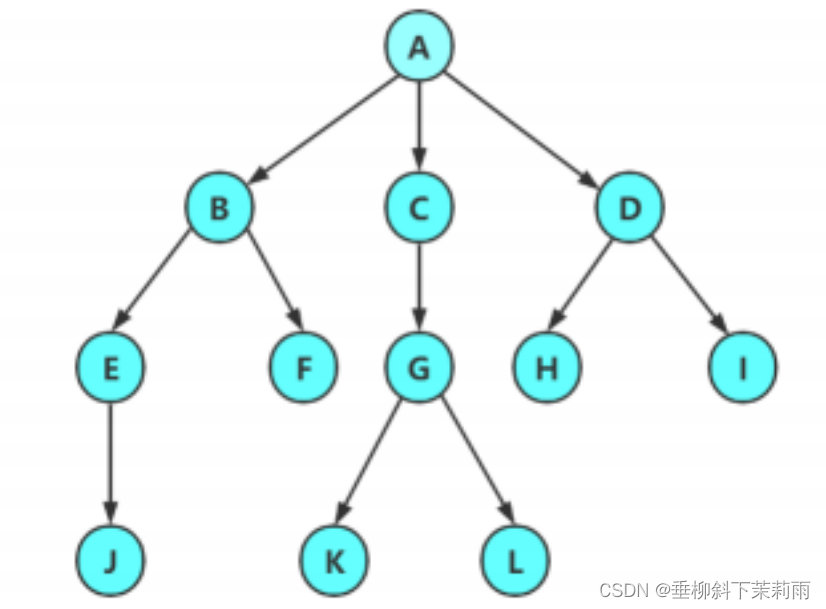
给定一棵包含N 个结点的多叉树，结点从1 至N 编号，其中1 号结点是根，每个结点的父结点的编号比自己的编号小。
请你计算其通过“左孩子右兄弟” 表示法转化成的二叉树，高度最高是多少。
注：只有根结点这一个结点的树高度为0 。

输入描述：

输入的第一行包含一个整数N。以下N-1行，每行包含一个整数，依次表示2至N号节点的父节点编号。

输出描述：

输出一个整数表示答案。

示例：

输入：

5

1

1

2

输出：

4

二、题解

思路分析：

（1）如何将多叉树转换为二叉树？

根据题目描述，通过“左孩子右兄弟”表示法进行转换，即节点node的孩子节点为node的左孩子，node的兄弟为node的右孩子

（2）如何使得转换后的二叉树高度最大？

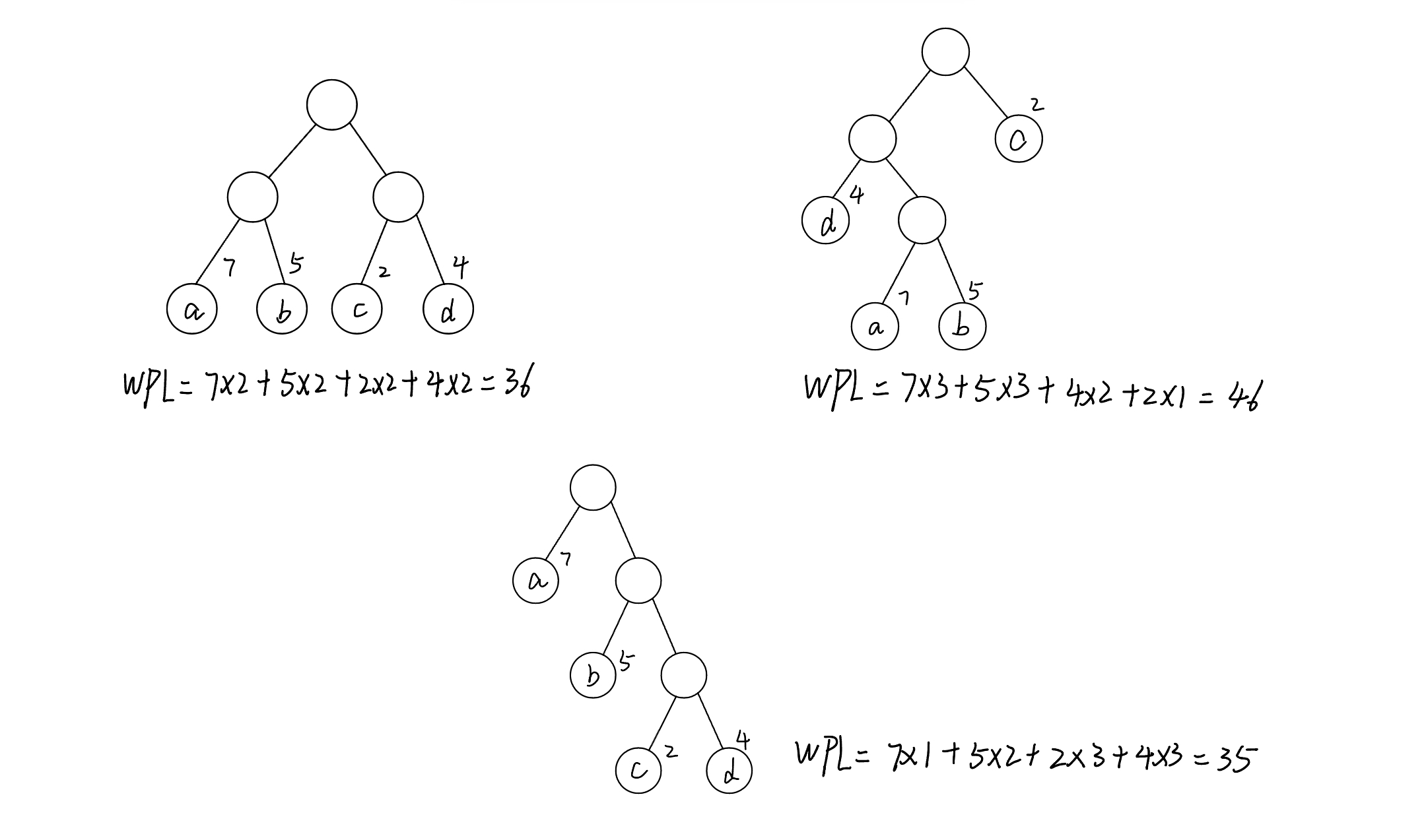
题目要求我们求得转换后的二叉树的最大高度，由于每个结点可以选任意子结点作为左孩子，并按任意顺序连接右兄弟。因此，我们需要找出高度更大的选择方式，通过画图分析，我们可以发现：选择孩子节点最多的兄弟节点作为尾节点，可以使二叉树的深度最大

（3）如何求最大高度？

按照（2）中的思路和上图分析，我们可以发现：

一个节点的最大高度 = 其孩子节点的个数 + 其孩子节点的最大高度，

因此，我们可以通过递归的方式来求出二叉树的最大高度

二叉树的最大高度 = 根节点的孩子节点数 + 其孩子节点的最大高度

而递归的出口则是 节点node的孩子节点个数为0

实现步骤：

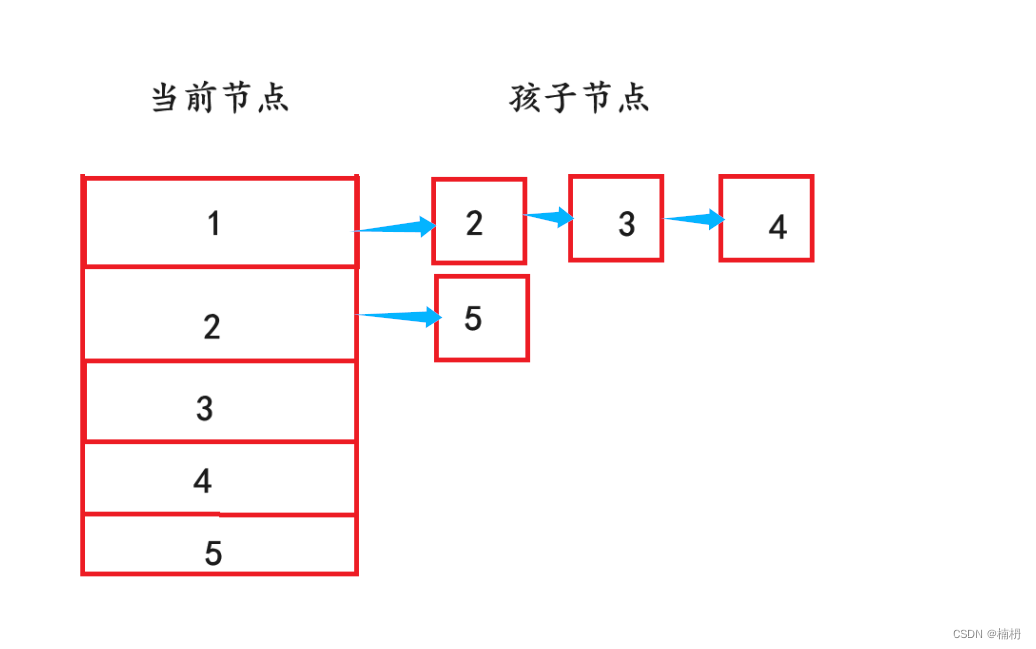
（1）定义一个ArrayList类型的数组，用于存放当前节点及其孩子节点，类似于邻接表

代码实现： 

public class Main {
    //定义一个ArrayList类型的数组,ArrayList中存放的是Integer类型的元素(当前节点的孩子节点)
    //由于递归时要访问数组中的元素(通过数组找到当前节点)，因此不能将数组定义为局部变量，
    // 而应该定义为成员变量
    public static ArrayList<Integer>[] lists;
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        //在此输入您的代码...
        int n = scan.nextInt();
        //创建数组
        lists = new ArrayList[n+1];
        for (int i = 0; i < n+1; i++) {
            lists[i] = new ArrayList<&gt;();
        }
        //存入孩子节点
        for (int i = 2; i <= n; i++) {
            int node = scan.nextInt();
            lists[node].add(i);//存储该节点的字节点
        }
        scan.close();
}

（2）通过递归的方式求二叉树的最大高度

若前节点node的孩子节点个数为0，则递归结束

若不为0，则遍历Arraylsit，分别求得其孩子节点的最大高度，并找出其最大值

节点的最大高度为node的孩子节点个数 + 孩子节点的最大高度

代码实现：

//利用递归求树的最大高度
public static int dsf(int node){
   int count = 0;
    //孩子节点的个数
   int size = lists[node].size();
   if(size == 0){
       return 0;
   }
    //若有孩子节点，则遍历孩子节点，找到孩子节点的最大高度
    for (int i = 0; i < size; i++) {
        count = Math.max(count,dsf(lists[node].get(i)));
    }
    return count+size;
}

完整代码：

import java.util.ArrayList;
import java.util.Scanner;
// 1:无需package
// 2: 类名必须Main, 不可修改

public class Main {
  //定义ArrayList类型的数组,ArrayList中存放的是Integer类型的元素
    public static ArrayList<Integer&gt;[] lists;
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        //在此输入您的代码...
        int n = scan.nextInt();
        lists = new ArrayList[n+1];
        for (int i = 0; i < n+1; i++) {
            lists[i] = new ArrayList<Integer>();
        }
        for (int i = 2; i <= n; i++) {
            int node = scan.nextInt();
            lists[node].add(i);//存储该节点的孩子节点
        }
        int count = dsf(1);
        System.out.println(count);
        scan.close();
    }

    //利用递归求树的最大高度
    public static int dsf(int node){
       int count = 0;
       //孩子节点的个数
       int size = lists[node].size();
       if(size == 0){
           return 0;
       }
       //若有孩子节点，则遍历孩子节点，找到孩子节点的最大高度
        for(int i = 0; i < size; i++) {
            count = Math.max(count,dsf(lists[node].get(i)));
        }
        return count+lists[node].size();
    }
}

题目来自：

左孩子右兄弟 – 蓝桥云课 (lanqiao.cn) 

代码007普通

打赏 收藏 海报 链接