本文介绍: 总之,由于递归调用堆栈,空间复杂度为O(n)。每个级别的递归都贡献了恒定的空间,但级别的数量与链表的长度成比例。-因此,“reverseList3”函数的总体空间复杂度为O(n),其中n是链表的长度。-在每个递归级别,函数都使用常量空间(局部变量:“tail”、“head”)。-由于递归的深度是O(n),因此这些变量贡献的空间复杂度也是O(n)。-因此,调用堆栈贡献的空间复杂度是O(n),其中n是链表的长度。-该函数是递归的,每次递归调用都会向调用堆栈添加一个新帧。-递归的深度取决于链表的长度。
时间复杂度: O(n), 空间复杂度:O(1)
时间复杂度: O(n), 空间复杂度:O(n)

为什么空间复杂度为O(n)?
要计算给定“reverseList”函数的空间复杂度,让我们分析内存使用情况:
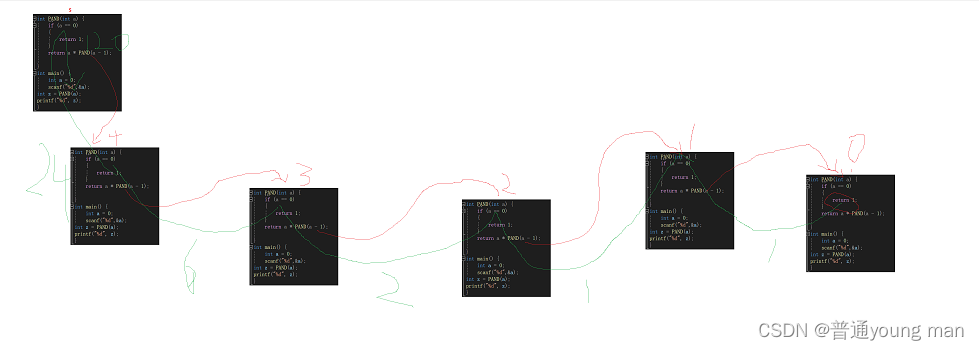
1.函数调用堆栈:
-该函数是递归的,每次递归调用都会向调用堆栈添加一个新帧。
-递归的深度取决于链表的长度。
-在每个递归级别,函数都使用常量空间(局部变量:“tail”、“head”)。
-因此,调用堆栈贡献的空间复杂度是O(n),其中n是链表的长度。
2.局部变量(`tail`,`head`):
-该函数为每个递归级别使用两个本地指针(“tail”和“head”)。
-这些变量所使用的空间在每个级别上都是恒定的。
-由于递归的深度是O(n),因此这些变量贡献的空间复杂度也是O(n)。
3.总体空间复杂性:
-空间复杂性的主要因素是递归导致的调用堆栈。
-因此,“reverseList3”函数的总体空间复杂度为O(n),其中n是链表的长度。
总之,由于递归调用堆栈,空间复杂度为O(n)。每个级别的递归都贡献了恒定的空间,但级别的数量与链表的长度成比例。
不好的案例
时间复杂度O(n^2), 空间复杂度O(1)
声明:本站所有文章,如无特殊说明或标注,均为本站原创发布。任何个人或组织,在未征得本站同意时,禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益,可联系我们进行处理。