【算法每日一练]-图论（保姆级教程篇6（图上dp））#最大食物链 #游走

题目：最大 食物链

解法一：

我们标记f[i]是被f[x]捕食的点对应的类食物链数

不难得出： f[x]=∑(f[i])
首先从生产者开始，每去掉一个被捕食的点，那么相邻捕食者就要加上去掉点的类食物链数，但是我们还需要找到出度为0的消费者。
所以这道题，我们要同时记录入度，还有出度（其实单纯的top o 排序就用不上出度，记录出度是为了找食物链结尾的个数）

#include&lt;bits/stdc++.h&gt; 
using namespace std;
const int MOD=80112002,M=500005,N=5005;
vector &lt;int&gt;v[N];
queue&lt;int&gt; q;
int n,m,ans,f[N],in[N],out[N];//我们需要标记每个点的入度和出度，f为以该点结尾的类食物链数
int main(){
	cin&gt;&gt;n&gt;>m;int x,y;
	for(int i=1;i<=m;i++){
		cin>>x>>y;
		v[x].push_back(y);//y吃x，x指向y
		out[x]++;in[y]++;
	}
	for(int i=1;i<=n;i++){//找到所有没有入度的点为起点
		if(in[i]==0){q.push(i);f[i]=1;}
	}
	while(q.size()){//进行拓扑排序
		int cur=q.front();q.pop();
		for(int i=0,sz=v[cur].size();i<sz;i++){
			int t=v[cur][i];
			f[t]=(f[t]+f[cur])%MOD;in[t]--;//去掉cur点的话，就要把f[cur]加到捕食它的点上
			if(in[t]==0) q.push(t);
		}		
	}
	for(int i=1;i<=n;i++){
		if(out[i]==0)ans=(ans+f[i])%MOD;//出度为0的点的f是我们要的真正食物链数
	}
	cout<<ans;
	return 0;
}

解法二：记忆化


#include <bits/stdc++.h>    //记忆化搜索
using namespace std;
const int N=1e5+5;
int n,m,ans,tot,in[N],out[N],f[N];
vector<int>ve[N];
int dfs(int x){//就是从每个生产者开始，看看能到多少个最终消费者，然后记忆化，最终计算所有生产者就是答案
	if(f[x])return f[x];
	if(!out[x])return 1;
	for(int i=0,sz=ve[x].size();i<sz;i++){
		int v=ve[x][i];
		f[x]+=dfs(v);
	}
	return f[x];
}
int main(){
	cin>>n>>m;int u,v,w;
	while(m--){
		cin>>u>>v;
		ve[u].push_back(v);
		out[u]++;in[v]++;
	}
	for(int i=1;i<=n;i++){
		if(in[i]==0&amp;&amp;out[i])
		ans+=dfs(i);
	}
	cout<<ans;
}

题目：游走

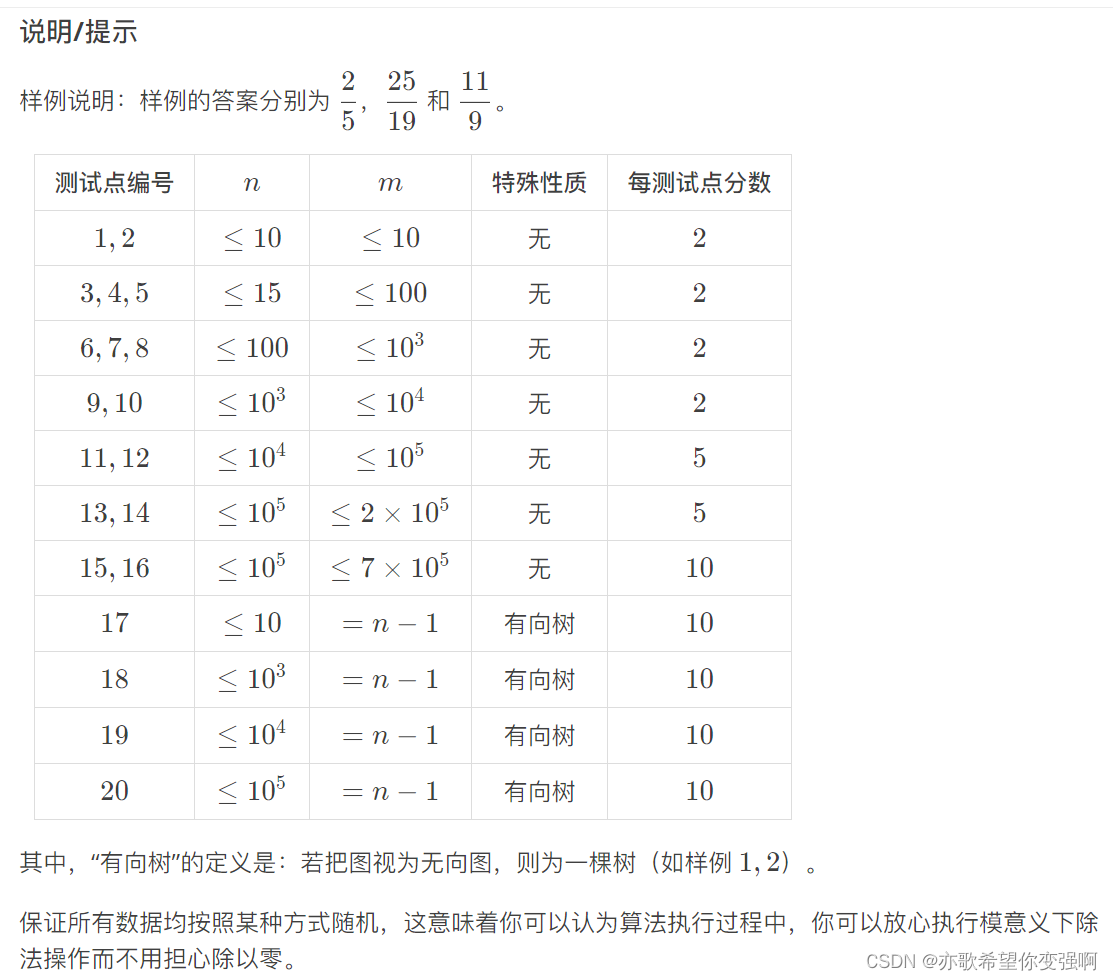
思路：

给一个DAG(有向无环图)，求所走路径长度的期望呗！也就是：所有路径长度总和/所有路径个数（因为每条路径概率都一样嘛）

明明是DAG图，topo一下完事了

我们设置g[i]表示以i为终点的路径数，f[i]表示i为终点的长度和

topo：从点j到一个点i，则g[i]+=g[j],f[i]+=f[j]+g[i]（因为啊，从j到i的每个路径长度都只增加1就行，一共增加了g[i]）

最后就是求(L/S)MOD，也就是L*(S^(MOD-2))MOD即可（逆元小知识）

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MAXN=1e5+5;
const ll MOD=998244353;
int n,m;
ll L,S,f[MAXN],g[MAXN];//g[i]表示以i为终点的路径数，f[i]表示i为终点的长度和
vector<int> edge[MAXN];
int in[MAXN],vis[MAXN];
void topo(void)//模板
{
	queue<int> q;
	for(int i=1;i<=n;i++)
    if(!in[i]) q.push(i);
    while(!q.empty())
    {
    	const int u=q.front();
    	q.pop();
    	if(vis[u]) continue; vis[u]=true;//没有环，所以这句话可以不要
    	for(auto v:edge[u])
    	{
    		in[v]--;
    		if(!in[v])	q.push(v);
    		f[v]=(f[v]+f[u]+g[u])%MOD;
    		g[v]=(g[v]+g[u])%MOD;
		}
	}
}

ll qpow(ll base,ll k)//快速幂求逆元
{
	ll res=1;
	while(k)
	{
		if(k&amp;1)	res=res*base%MOD;
		base=base*base%MOD;
		k>>=1;
	}
	return res;
}

int main()
{
	cin>>n>>m;
	for(int i=1;i<=m;i++)
	{
		int u,v;cin>>u>>v;
		edge[u].push_back(v);
		in[v]++;
	}
	for(int i=1;i<=n;i++)	g[i]=1;//初始化:每个点的路径数初始化为1
	topo();
	for(int i=1;i<=n;i++)	L=(L+f[i])%MOD;//获取最终的总长度
	for(int i=1;i<=n;i++)	S=(S+g[i])%MOD;//获取最终的路径个数
	cout<<(L*qpow(S,MOD-2))%MOD<<endl;//求L/S的结果，即L*S的逆元，即L*S^(MOD-2)
	return 0;
}

提一嘴：

为什么要引入逆元呢？
因为(a+b)%MOD=(a%MOD+b%MOD)%MOD
(a-b)%MOD=(a%MOD-b%MOD)%MOD
(a*b)%MOD=(a%MOD*b%MOD)%MOD


但是除法不满足，我们要求(a/b)%p=1等价于(a*x)%p=1，这个x就是b的乘法逆元（可以理解成x为1/b），也就是(b*x)%p=1


再引入费马小定理：假如a和p互质，那么a^(p-1)=1(%p)，故a*a^(p-2)=1(%p)，故a的逆元x=a^(p-2)%p
因此：(x/y)%p等价于x*y^(p-2)%p，注意每乘一次就要去一次模