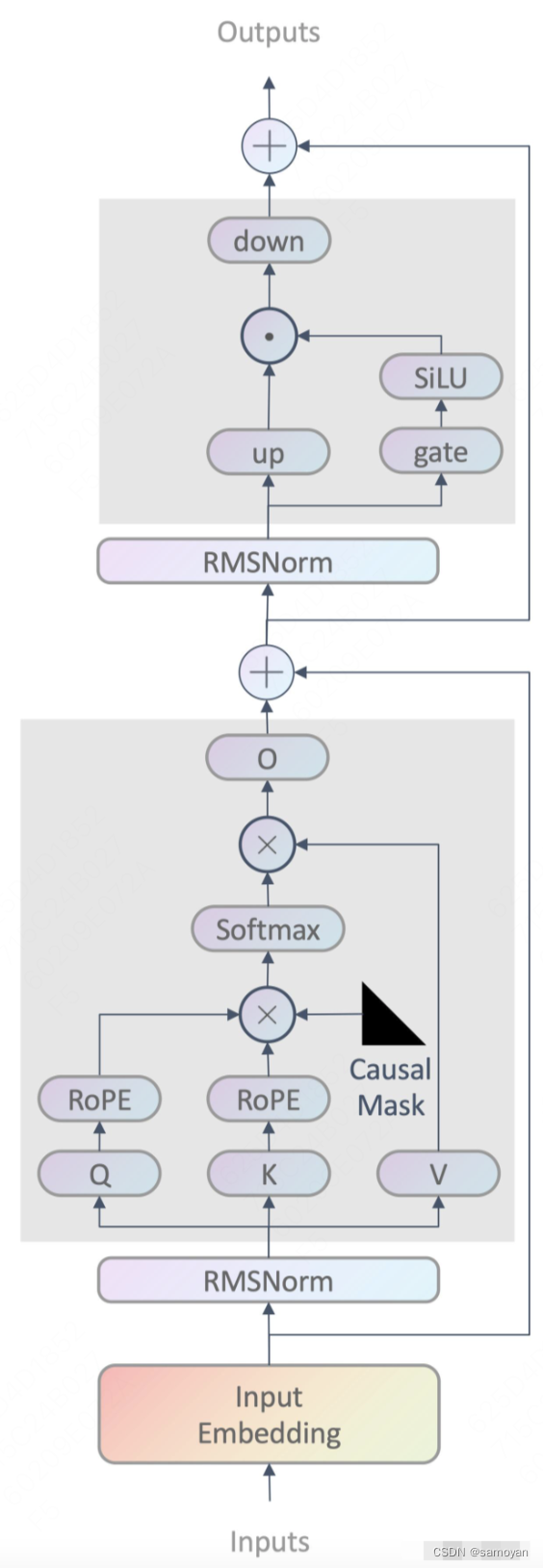
本文介绍: 逻辑回归模型是一种常用的统计建模方法，用于处理二元分类问题，即将实例划分为两个类别：正类和负类。它的主要思想是在每个实例上建立一个概率模型，以估计其属于正类的概率。在逻辑回归模型中，首先定义一个非线性的激活函数，如Sigmoid函数，用于处理输入特征向量与权重向量的内积。然后，通过对这些概率进行最大化或最小化来求解模型参数的最佳值。逻辑回归模型的优点是计算简单，解释性强，易于理解。但缺点是容易过拟合，且不能很好地处理多分类问题。因此，通常情况下，需要与其他技术相结合，如正则化和集成学习等，来改善模型。
⎧wt+1=wt−nα∑i=1n(pi(t)−yi)xibt+1=bt−nα∑i=1n(pi(t)−yi)
其中，
i
(
t
)
=
1
1
+
(
−
(
⟨
w
t
,
i
⟩
+
t
)
)
编程求解
import numpy as np
def sigma_fun(z):
z = z.astype('float')
z_ravel = z.ravel() # 将 numpy 数组展平
length = len(z_ravel)
ls = []
for index in range(length):
if z_ravel[index] >= 0:
ls.append(1.0 / (1 + np.exp(-z_ravel[index])))
else:
ls.append(np.exp(z_ravel[index]) / (np.exp(z_ravel[index]) + 1))
return np.array(ls).reshape(z.shape)
def cross_entropy(y, p):
return -(y * np.log(p + 0.0000001) + (1 - y) * np.log(1 - p + 0.0000001))
def gradient_descent(X, y, W, b, alpha, t):
for i in range(t):
z = np.dot(X, W) + b
p = sigma_fun(z)
loss = cross_entropy(y, p)
print('第 {} 次迭代的权重参数为：{}'.format(i, W.round(6).tolist()))
print('第 {} 次迭代的偏置参数为：{}'.format(i, b))
print('第 {} 次迭代的平均损失为：{}'.format(i, np.mean(loss).round(6)))
nablaLW = np.sum((p - y) * X, axis=0).reshape(X.shape[1], 1)
W = W - (alpha / X.shape[0]) * nablaLW
nablaLb = np.sum(p - y)
b = b - (alpha / X.shape[0]) * nablaLb
print('第 {} 次迭代的梯度参数 W 为：{}'.format(i, nablaLW.round(6).tolist()))
print('第 {} 次迭代的梯度参数 b 为：{}n'.format(i, nablaLb))
X = np.array([[0.5, 1], [1, 2], [-0.2, 1], [1, -3]])
y = np.array([[0], [1], [1], [0]])
b = -1
W = np.ones((X.shape[1], 1))
alpha = 0.5
print('步长 α 为：{}n'.format(alpha))
gradient_descent(X, y, W, b, alpha, 6)
# output
步长 α 为：0.5
第 0 次迭代的权重参数为：[[1.0], [1.0]]
第 0 次迭代的偏置参数为：-1
第 0 次迭代的平均损失为：0.486933
第 0 次迭代的梯度参数 W 为：[[0.349419], [-0.308058]]
第 0 次迭代的梯度参数 b 为：0.0008482850448257445
第 1 次迭代的权重参数为：[[0.956323], [1.038507]]
第 1 次迭代的偏置参数为：-1.0001060356306033
第 1 次迭代的平均损失为：0.480379
第 1 次迭代的梯度参数 W 为：[[0.345769], [-0.265492]]
第 1 次迭代的梯度参数 b 为：0.013170440015569933
第 2 次迭代的权重参数为：[[0.913102], [1.071694]]
第 2 次迭代的偏置参数为：-1.0017523406325495
第 2 次迭代的平均损失为：0.474592
第 2 次迭代的梯度参数 W 为：[[0.341829], [-0.232955]]
第 2 次迭代的梯度参数 b 为：0.02239339071628172
第 3 次迭代的权重参数为：[[0.870373], [1.100813]]
第 3 次迭代的偏置参数为：-1.0045515144720847
第 3 次迭代的平均损失为：0.469342
第 3 次迭代的梯度参数 W 为：[[0.337668], [-0.207736]]
第 3 次迭代的梯度参数 b 为：0.02924657055932656
第 4 次迭代的权重参数为：[[0.828164], [1.12678]]
第 4 次迭代的偏置参数为：-1.0082073357920005
第 4 次迭代的平均损失为：0.464489
第 4 次迭代的梯度参数 W 为：[[0.333348], [-0.187982]]
第 4 次迭代的梯度参数 b 为：0.03428385214987886
第 5 次迭代的权重参数为：[[0.786496], [1.150278]]
第 5 次迭代的偏置参数为：-1.0124928173107353
第 5 次迭代的平均损失为：0.459943
第 5 次迭代的梯度参数 W 为：[[0.328922], [-0.172379]]
第 5 次迭代的梯度参数 b 为：0.03792999829875388
sklearn 实现，并查看拟合指标
from sklearn.linear_model import LogisticRegression as LR
import pandas as pd
import numpy as np
X = np.array([[0.5, 1], [1, 2], [-0.2, 1], [1, -3]])
y = np.array([0, 1, 1, 0])
lr = LR()
lr.fit(X, y)
predicted = lr.predict(X)
print('预测值：', predicted)
Accuracy = ((predicted == y).sum() / len(y))
print('准确率：', Accuracy)
TP = sum((y == 1) & (predicted == 1))
FP = sum((y == 0) & (predicted == 1))
Precision = TP / (TP + FP)
print('精确率：', round(Precision, 3))
Recall = ((predicted == y).sum() / y.sum()).round(3)
print('召回率：', Recall)
F1 = 2 * Precision * Recall / (Precision + Recall)
print('F1 score值：', round(F1, 3))
# output
预测值： [1 1 1 0]
得分： 0.75
准确率： 0.75
精确率： 0.667
召回率： 1.5
F1 score值： 0.923
原文地址:https://blog.csdn.net/qq_61828116/article/details/134656543
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
如若转载，请注明出处：http://www.7code.cn/show_21642.html
如若内容造成侵权/违法违规/事实不符，请联系代码007邮箱：suwngjj01@126.com进行投诉反馈，一经查实，立即删除！
声明：本站所有文章，如无特殊说明或标注，均为本站原创发布。任何个人或组织，在未征得本站同意时，禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益，可联系我们进行处理。
