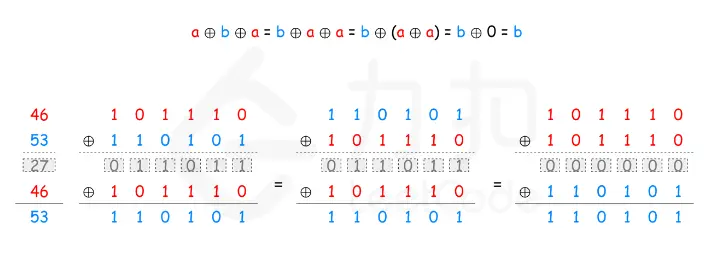
本文介绍: 不重复的存储数组的元素,也就是每个元素只存储一次,重复的不存储,计算它们的和,就相当于所有数字的两倍之和。然后将原数组中的元素全部相加,就相当于只出现了一次的元素加上全部出现了两次的元素。遍历数组中的每个数字,如果集合中没有该数字,则将该数字加入集合,如果集合中已经有该数字,则将该数字从集合中删除,最后剩下的数字就是只出现一次的数字。遍历数组即可得到每个数字出现的次数,并更新哈希表,最后遍历哈希表,得到只出现一次的数字。因此,数组中的全部元素的异或运算结果即为数组中只出现一次的数字。
136. 只出现一次的数字
题目:
给你一个 非空 整数数组 nums ,除了某个元素只出现一次以外,其余每个元素均出现两次。找出那个只出现了一次的元素。
你必须设计并实现线性时间复杂度的算法来解决此问题,且该算法只使用常量额外空间。
示例:
示例 1 :
示例 2 :
示例 3 :
提示:
解题:
方法一:集合法
方法二:哈希表法
方法三:元素之和两倍性质
方法四:位运算(线性时间复杂度,常数空间复杂度)
声明:本站所有文章,如无特殊说明或标注,均为本站原创发布。任何个人或组织,在未征得本站同意时,禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益,可联系我们进行处理。