本文介绍: 牛顿迭代法(Newton‘s method)又称为牛顿-拉夫逊(拉弗森)方法(Newton-Raphson method),它是牛顿在17世纪提出的一种在实数域和复数域上近似求解方程的方法。牛顿迭代法实质是一种求根算法,这意味着它的目标是找到函数 f(x)=0 的值 x。在几何上可以将其视为 x 的值,这时函数与 x 轴相交。
1 基本介绍
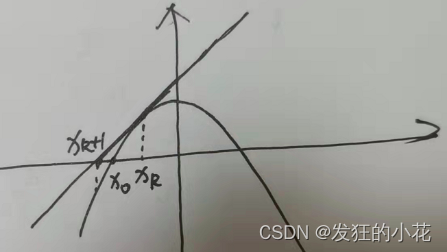
2 公式推导
3 牛顿迭代法的应用
3.1 求倒数
3.2 开根号
3.2 马克尔的方法
4 收敛性分析
声明:本站所有文章,如无特殊说明或标注,均为本站原创发布。任何个人或组织,在未征得本站同意时,禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益,可联系我们进行处理。





![[软件工具]文档页数统计工具软件pdf统计页数word统计页数ppt统计页数图文打印店快速报价工具](https://img-blog.csdnimg.cn/direct/09dfbaff3e9a47a9a551dd65fef5d482.jpeg)