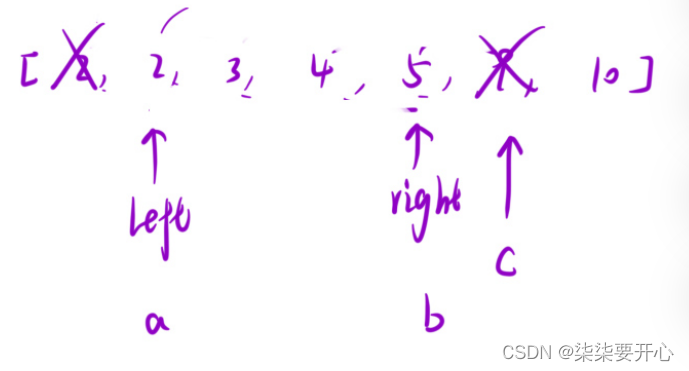
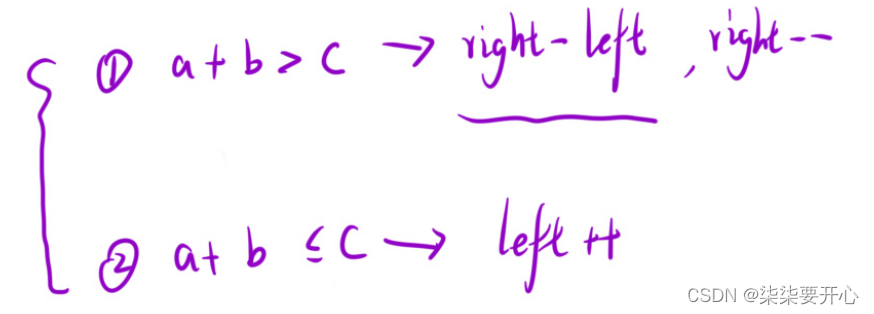
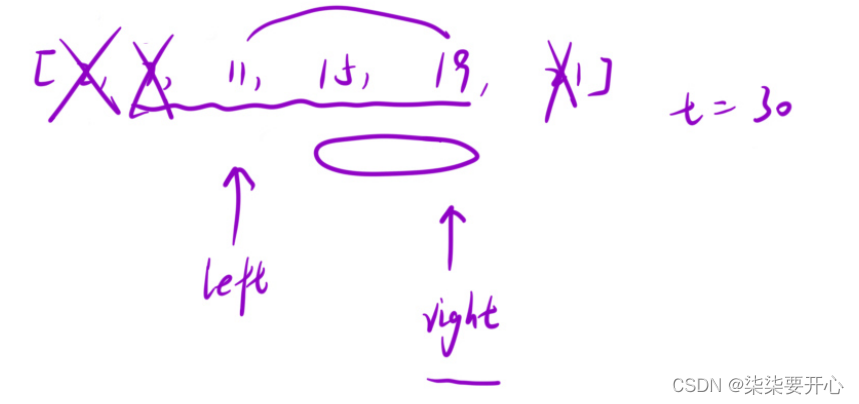
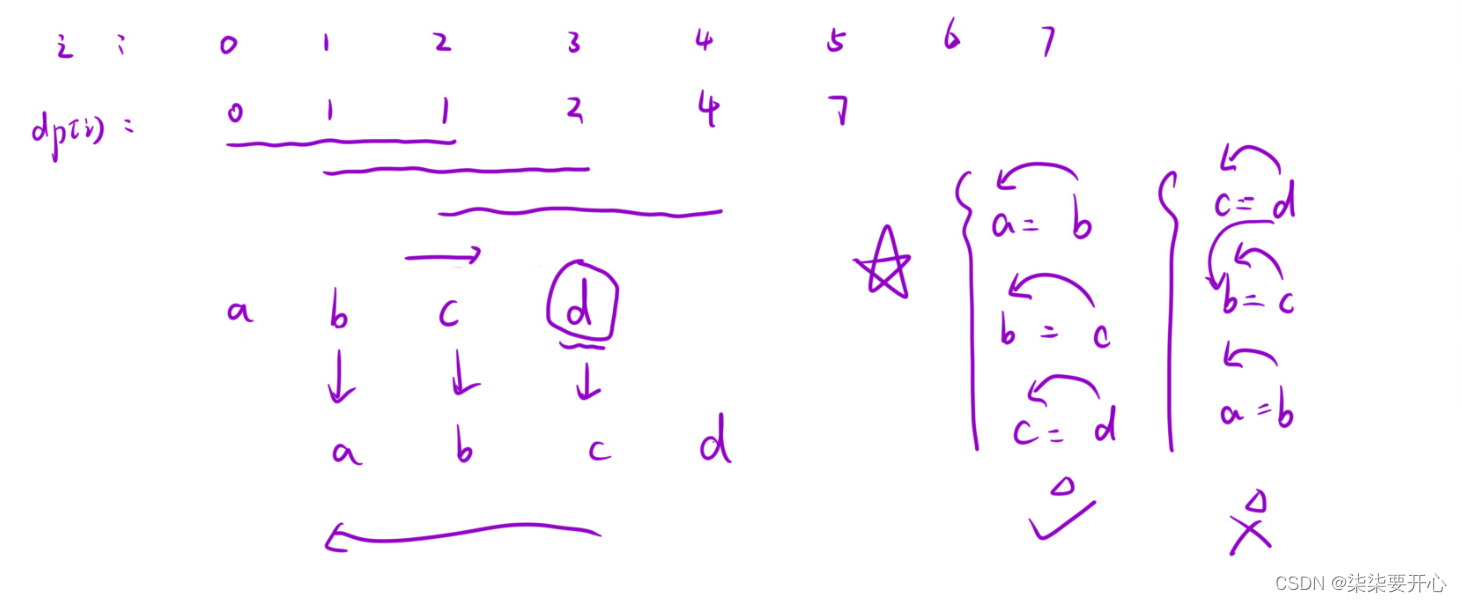本文介绍: 这个时候,我们想,如果让这个数组是有序的,对比的这三个边是有序的,那么两个较短的边相加,大于第三边,是不是就可以说明前面两条边任意一条和后面的相加,都大于其余一条边呢?让left + right,如果大于 最后一个数字,那么left 右边的所有数字和 right 相加都大于,所以中间的统计下来,right –我们一般的判断都是任意两边之和大于第三边,但是如果在时间复杂度的位置上考虑,比三次太麻烦。我们先看这个数组,我们先把最后一个数字固定,定义 left 和 right,如果 大于 t ,right–
611. 有效三角形的个数

题干:
首先看题干,非负整数数组,三元组数
所以,我们可知,这个数组最少有三个元素,这样才能组成三元组
在解题之前,我们补充一点:
给我们三个数,怎么判断是不是能不能构成三角形呢?
我们一般的判断都是任意两边之和大于第三边,但是如果在时间复杂度的位置上考虑,比三次太麻烦
这个时候,我们想,如果让这个数组是有序的,对比的这三个边是有序的,那么两个较短的边相加,大于第三边,是不是就可以说明前面两条边任意一条和后面的相加,都大于其余一条边呢?
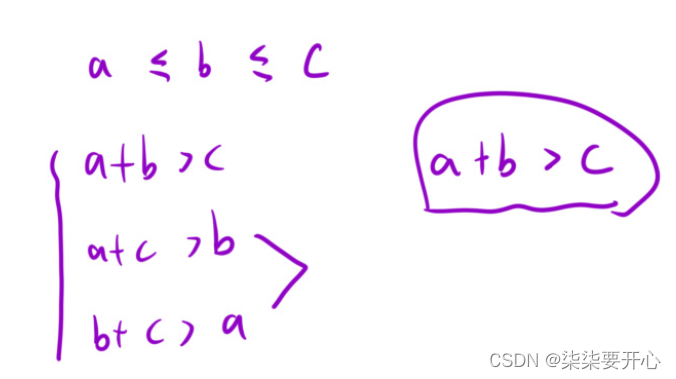
很明显,这样是可以的,所以我们的算法就进一步进行了优化
题解:
1、暴力枚举 O(N)
暴力算法就是写三个 for 循环嵌套,在最里面的一层 for 循环判断三个数是否能组成三角形
代码:
LCR 179. 查找总价格为目标值的两个商品
题干:
题解:
代码:
1137. 第 N 个泰波那契数
题干:
原理:
1、状态表示(dp表里面的值所表示的含义)
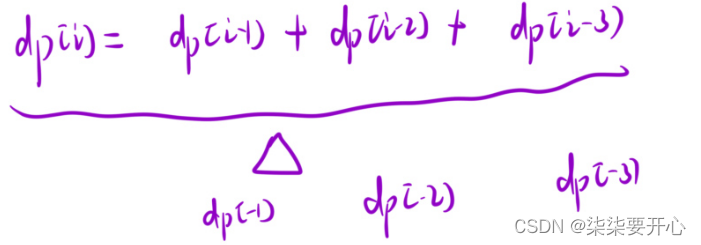
2、状态转移方程(dp[i] 等于什么)
3、引初始化 (保证填表的时候不越界)
4、填文顺表 (为了填写当前状态的时候,所需的状态已经计算过了)
5、返回值 (题目要求 + 状态表示)
代码:
空间优化:
声明:本站所有文章,如无特殊说明或标注,均为本站原创发布。任何个人或组织,在未征得本站同意时,禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益,可联系我们进行处理。