计算机视觉（OpenCV+TensorFlow）

计算机视觉（OpenCV+TensorFlow）

前言

本系列文章是OpenCV系列文章的第四篇，仍然跟随上篇内容主要聚焦于图像的一些操作，到本篇为止，与图像有关的所有的基本操作我们就都总结完了

7. 图像直方图

图像直方图顾名思义就是，x轴是像素值，y是像素的数量
下图就是一个图像直方图，像素值为250的数量大概是500个

Opencv给我们提供的函数是cv2.calcHist()，该函数有5个参数：

• image：输入图像，传入时应该用中括号括起来，也就是我们可以传入多张数据
• channels：传入图像的通道，如果是灰度图像，那只有一个通道，值为0，如果是彩色图像，那么值为0，1，2中选择一个，对应着BGR各个通道，这个值也要[]传入
• mask：掩膜图像，如果统计整幅图，那么为none,如果我们只是统计图的一部分的直方图，那就要构造相应的掩膜实现，这个之后我们再具体说
• histSize：灰度级的个数，需要中括号，比如[256]
• ranges：像素值的范围，通常[0,256]，有的图像如果不是，需要自己调整这个值

hist是256x1的数组，每个值对应于该图像中具有相应像素值的像素数

img = cv2.imread('cat.jpg',0) #0表示灰度图
hist = cv2.calcHist([img],[0],None,[256],[0,256])

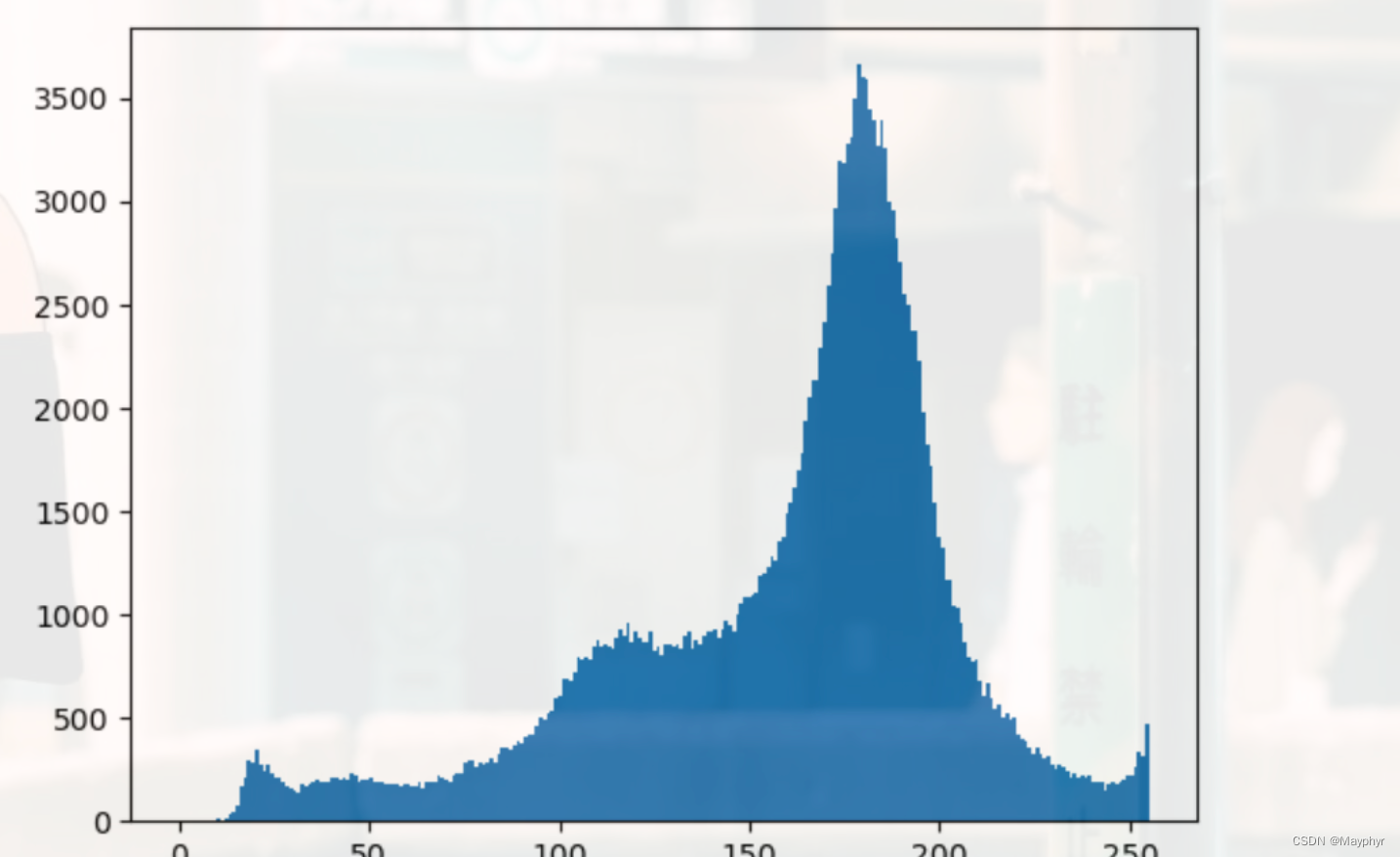
绘制直方图

绘制直方图有两种方式：

1. 使用Matplotlib
   1. Matplotlib带有直方图绘图功能：matplotlib.pyplot.hist()

它直接找到直方图并将其绘制。无需使用 calcHist() 或 np.histogram() 函数来查找直方图

img = cv2.imread('cat.jpg',0) #0表示灰度图
hist = cv2.calcHist([img],[0],None,[256],[0,256])
plt.hist(img.ravel(),256); 
plt.show()

2. 或者还可以使用Matplotlib的法线图

img = cv2.imread('cat.jpg') 
color = ('b','g','r')
for i,col in enumerate(color): 
    histr = cv2.calcHist([img],[i],None,[256],[0,256]) 
    plt.plot(histr,color = col) 
    plt.xlim([0,256]) 

2. 使用OpenCV，用OpenCV的话，就有点麻烦，还要对hist数组进行变化，所以就用Matplotlib就可以了。

掩膜

如果我们要查找图像某些区域的直方图，只需在要查找直方图的区域上创建白色图像，不查找的创建黑色。然后这个只有白色和黑色的图像就是一个掩膜。
掩膜其实就是用了与操作，因为要显示的区域掩膜上是255，255换算成二进制8个1，任何数跟1做与运算都是它本身，那也就是任何数跟255做与运算都是它本身，那这不就是保留了原来的值了嘛。而又因为不想保留的地方是黑色的，任何数与0做与运算都是0，所以就把不想保留的地方变成了黑色的

# 先创建一个都是0的数组，然后将部分区域变成白色
mask = np.zeros(img.shape[:2], np.uint8)
print (mask.shape)
mask[100:300, 100:400] = 255
cv_show(mask,'mask')
# 导入一张灰度图
img = cv2.imread('cat.jpg', 0)
# 相应位置做与运算
masked_img = cv2.bitwise_and(img, img, mask=mask)#与操作
# 传入mask，统计部分区域的图像直方图
hist_mask = cv2.calcHist([img], [0], mask, [256], [0, 256])

8. 直方图均衡化

https://blog.csdn.net/zaishuiyifangxym/article/details/89813977

直方图均衡化的介绍

** 直方图均衡化是一种简单有效的图像增强技术，通过改变图像的直方图来改变图像中各个像素的灰度，主要用于增强动态范围偏小的图像的对比度。原始图像由于其灰度分布可能集中在较窄的区间，造成图像不够清晰。**

例如，过曝光图像的灰度级集中在高亮度范围内，而曝光不足图像的灰度级集中在低亮度范围内。
** 通过直方图均衡化，可以把原始图像的直方图变换成均匀分布的形式，这样就增加了像素之间灰度值差别的动态范围，从而达到增强图像整体对比度的效果。**

简而言之，直方图均衡化的原理是：对在图像中像素个数多的灰度值（即对画面起主要作用的灰度值）进行展宽，而对像素个数少的灰度值（即对画面不起主要作用的灰度值）进行归并，从而增大对比度，使图像清晰。

直方图均衡化的步骤

1. 计算累计直方图
2. 将累计直方图进行区间转换
3. 在累计直方图中，概率相近的原始值会被处理为相同值

具体的例子：
** 如下图所示，已知一幅图像的像素分布为 7**

7，根据像素值，则可以计算出统计直方图

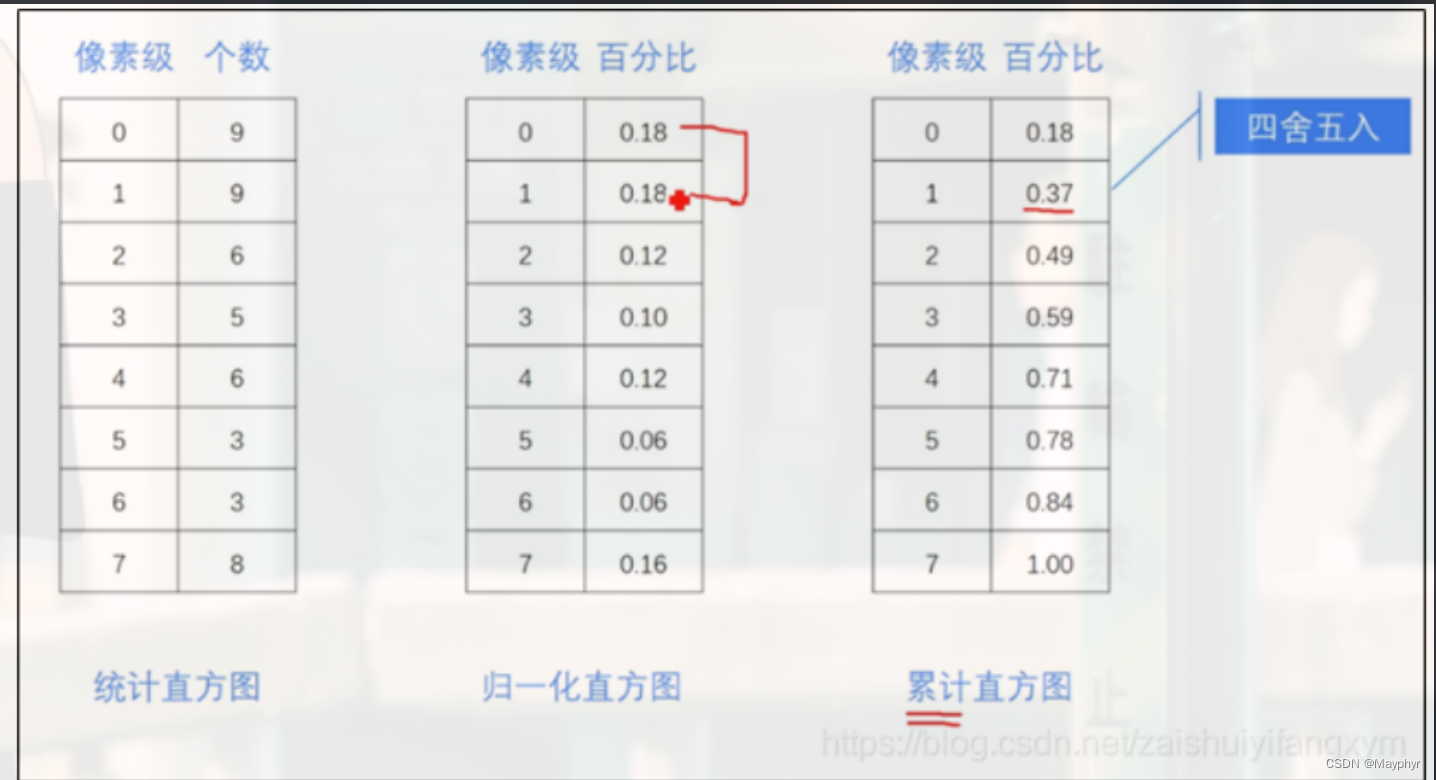
根据统计直方图，可以算出归一化直方图和累计直方图，如下图所示：

将累计直方图进行区间转换，如下图所示：

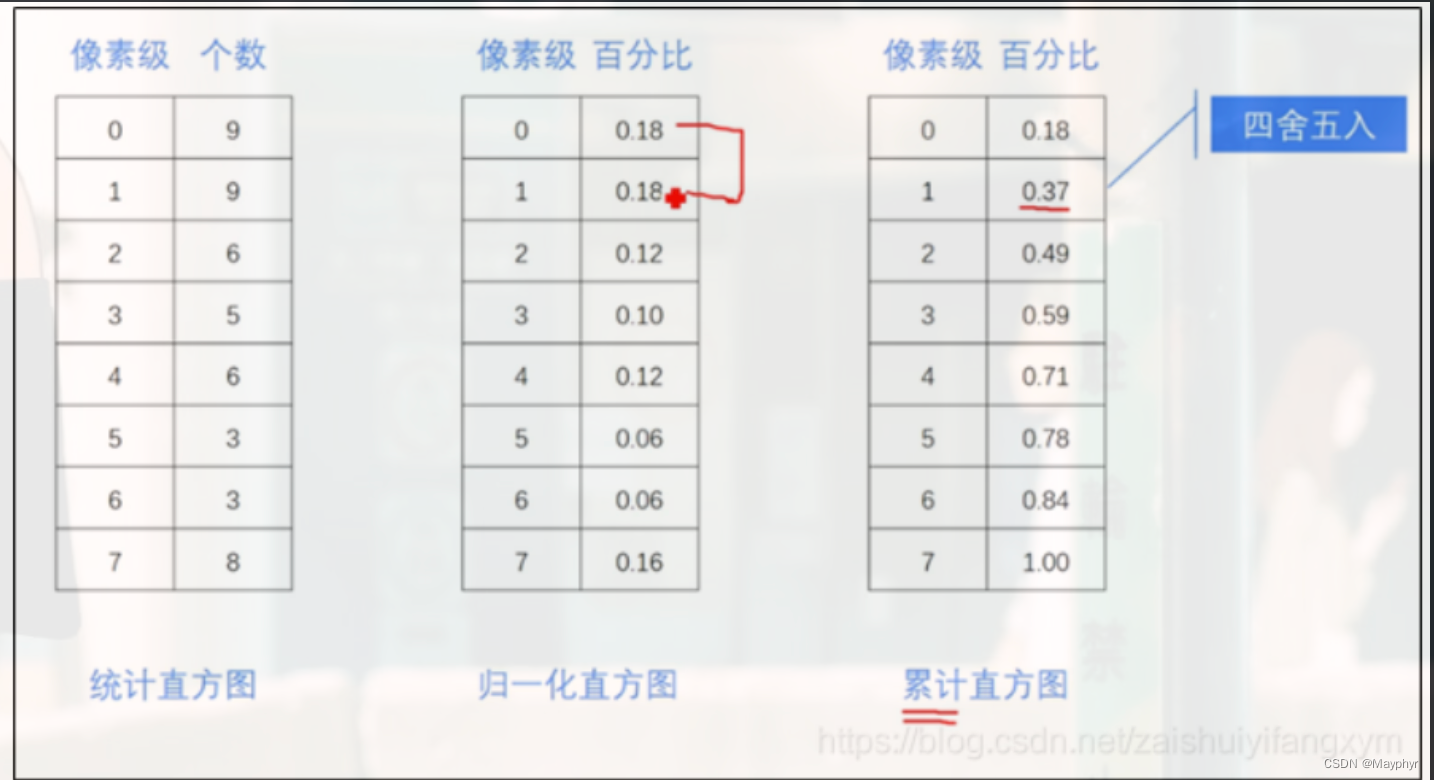
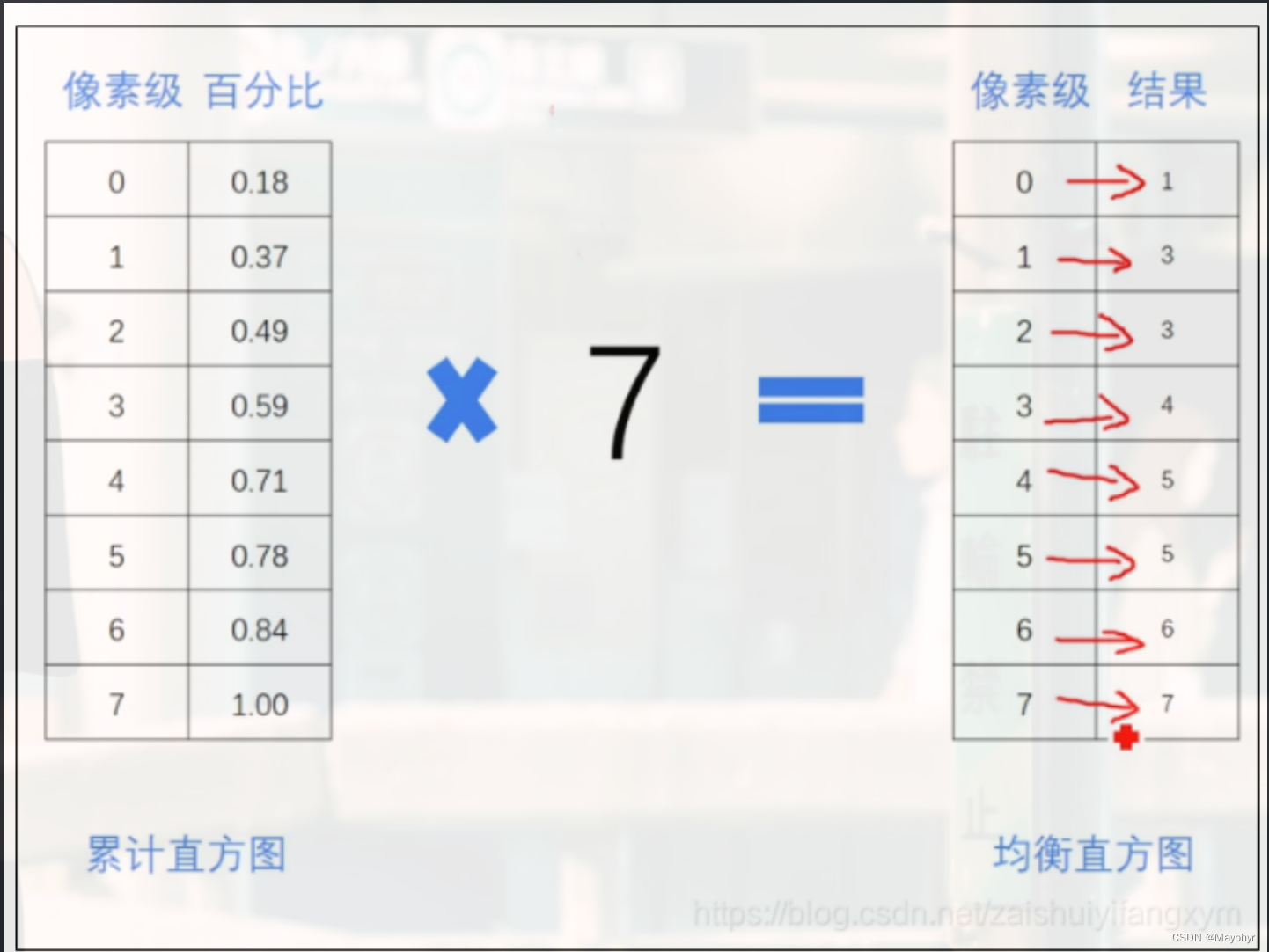
我们看均衡直方图，1对应3，这个3是说明像素级<=1的共有3个，那像素级为1的就有2个
2-0，3-1，4-1，5-0，6-1，7-1,我们可以看到有两个都是0，那相比于原来不就少了两个像素级嘛
上面的灰度级是8，那灰度级转变成256，计算方法类似，如下图所示：

!
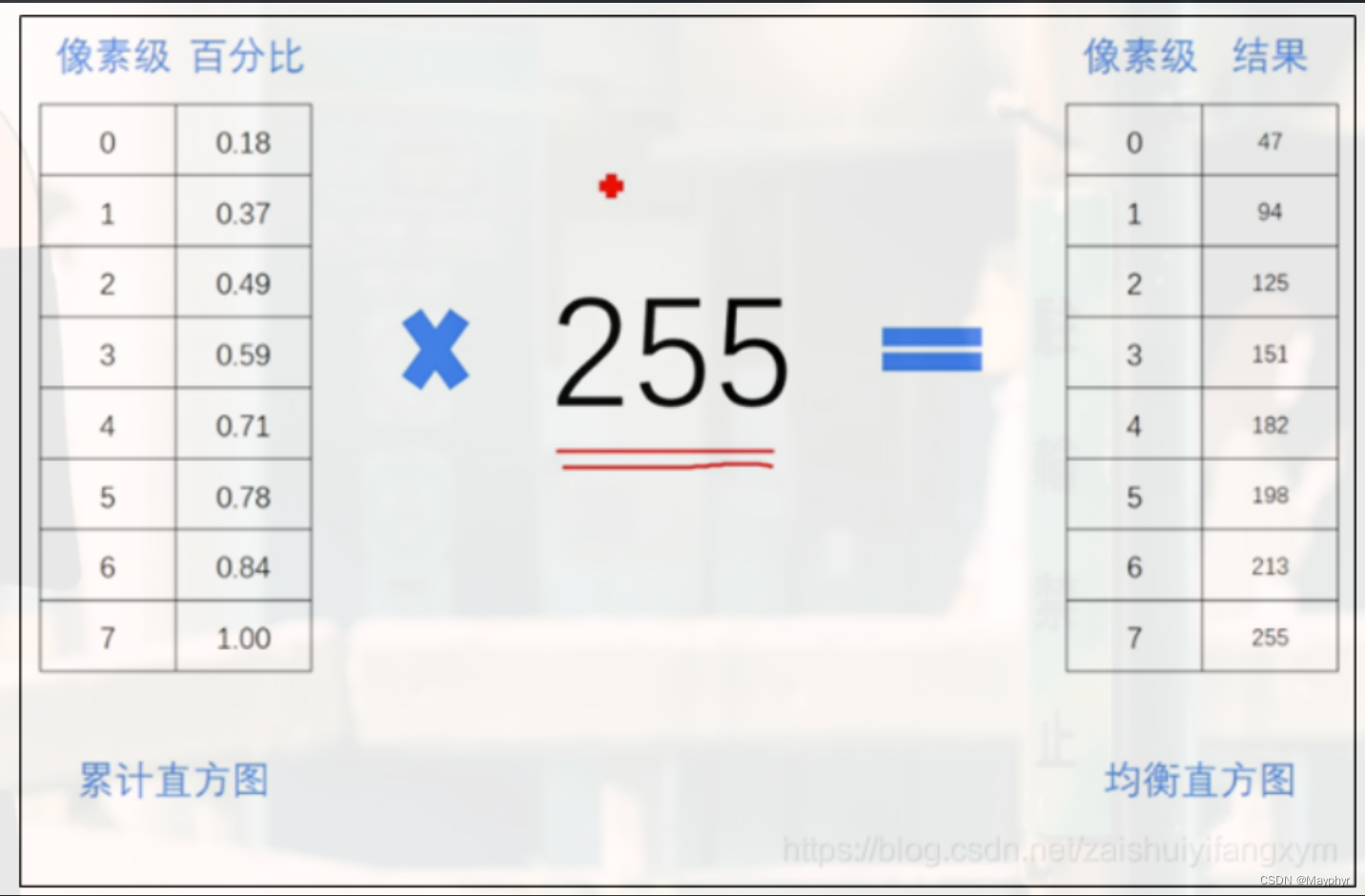
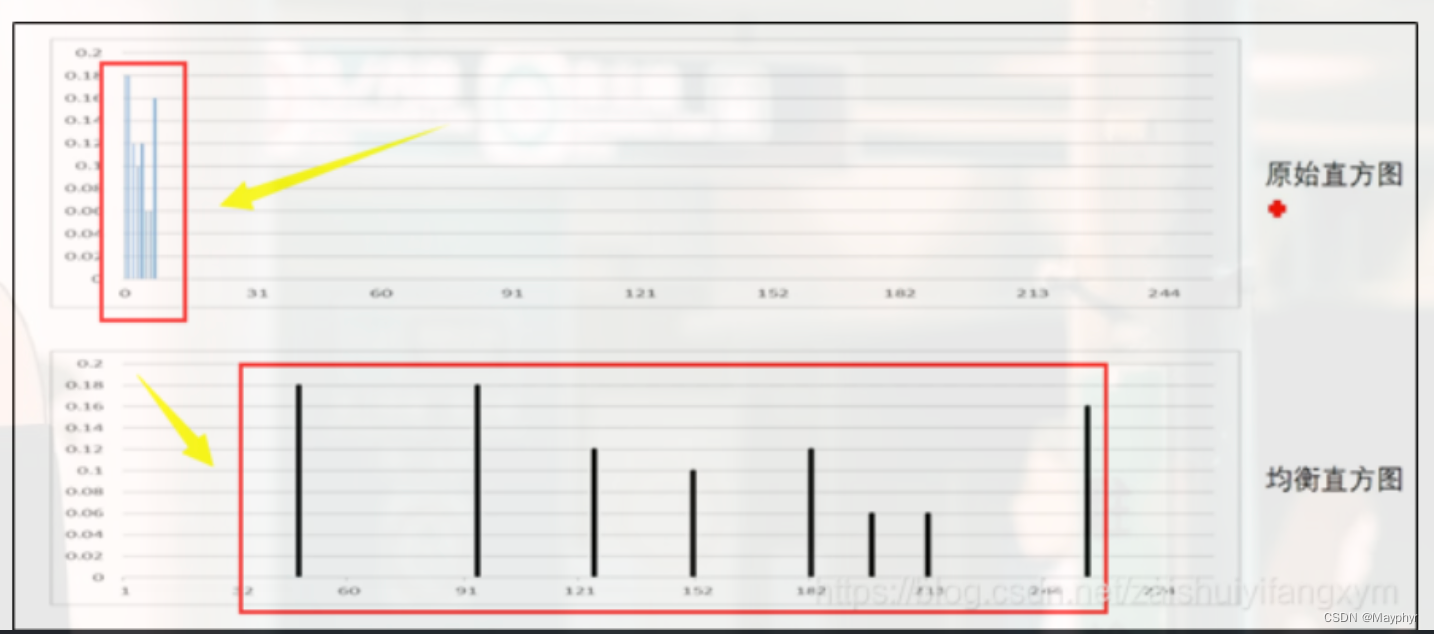
原始直方图和均衡直方图为

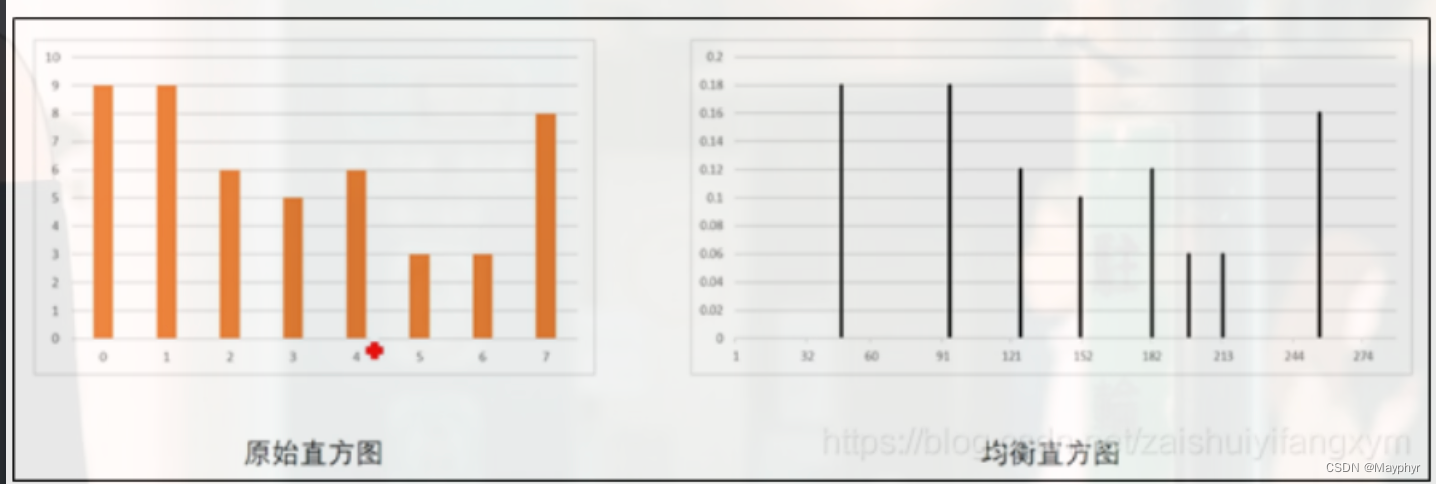
由上图可以看出，虽然二者相似，但右侧均衡化后的直方图分布更均匀，相邻像素级概率和与高概率近似相等。如果将两张图的灰度级放在同一区间，可以看出差别更大，如下图所示：

在OpenCV中，我们用 equ = cv2.equalizeHist(img) 这个函数就可以均衡化

# 均衡化之前
img = cv2.imread('clahe.jpg',0) #0表示灰度图 #clahe
plt.hist(img.ravel(),256); 
plt.show()
# 均衡化之后
equ = cv2.equalizeHist(img) 
plt.hist(equ.ravel(),256)
plt.show()

均衡化之前：

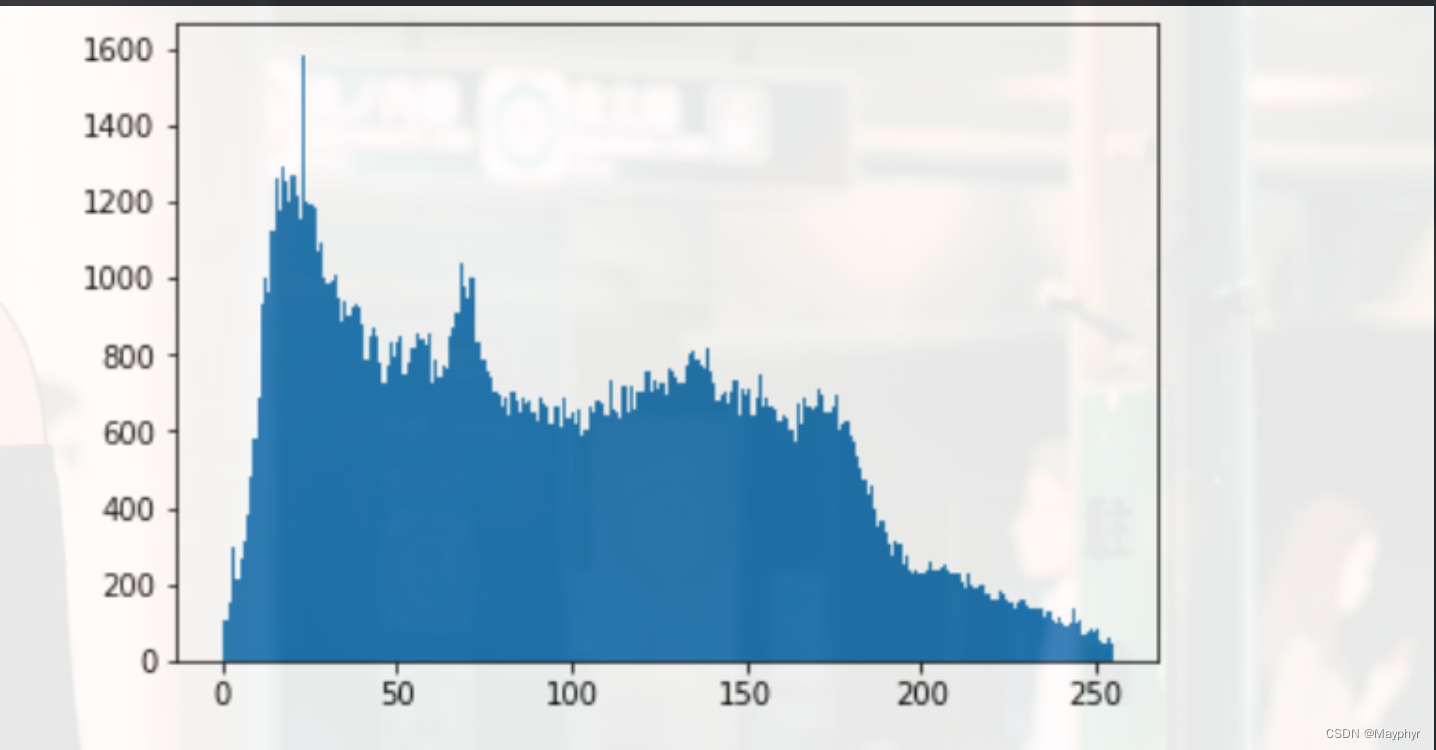
均衡化之后：

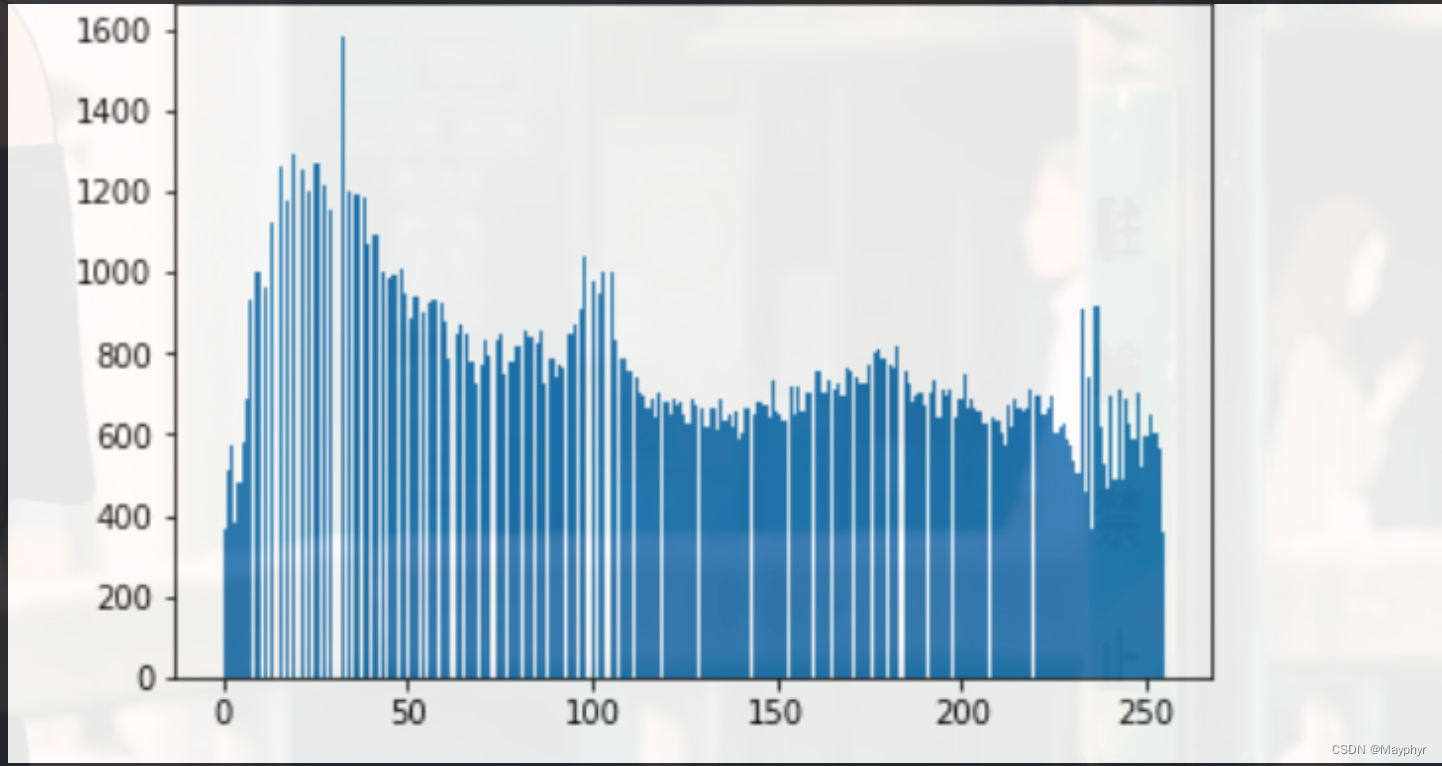
自适应直方图均衡化

下图是均衡化的前后对比，可以看到背景的对比度是增强了，但是雕像的脸却变亮了许多，我们在那里丢失了大多数的信息，这是因为均衡化是默认是对全图进行均衡化，我们也可以分模块进行均衡化，这样就可以处理的更好。

在OpenCV 中，我们用 clahe = cv2.createCLAHE(clipLimit=2.0, tileGridSize=(8,8)) 函数来做自适应变化

• titleGridSize 进行像素均衡化的网格大小，即在多少网格下进行直方图的均衡化操作
• clipLimit：颜色对比度限制阈值，默认为40；

# 创建一个clear对象
clahe = cv2.createCLAHE(clipLimit=2.0, tileGridSize=(8,8)) 
# 让图像交给clear对象处理
res_clahe = clahe.apply(img)

9. 图像转换

傅里叶变换

傅里叶变换，在很多领域都有很重要的运用，那么在图像处理中也有许多的运用，如果有朋友不是很了解的话，可以看下面这篇文章

https://zhuanlan.zhihu.com/p/19763358
傅里叶变换在图像中的运用：

1. 图像增强与图像去噪
2. 图像分割与边缘检测
3. 图像特征提取
4. 图像压缩

大家看傅里叶变换在图像中的运用我们或多或少在前都提到过，比如这个图像增强，图像去噪，图像分割和边缘检测，但是那些都是在时域上的操作，如果把图像放到频域中，那这些操作会更轻松。
简单来说：傅里叶变换的目的并不是为了观察图像的频率分布（至少不是最终目的），更多情况下是为了对频率进行过滤，通过修改频率以达到图像增强、图像去噪、边缘检测、特征提取、压缩加密等目的。

在频域中的图像

下面是图像在频域中的一些概念：

1. 图像的频率是表征图像中灰度变化剧烈程度的指标，是灰度在平面空间上的梯度
2. 图像高频分量：图像突变部分；在某些情况下指图像边缘信息，某些情况下指噪声，更多是两者的混合；
3. 低频分量：图像变化平缓的部分，也就是图像轮廓信息
4. 高通滤波器：让图像使低频分量抑制，高频分量通过
5. 低通滤波器：与高通相反，让图像使高频分量抑制，低频分量通过
6. 带通滤波器：使图像在某一部分的频率信息通过，其他过低或过高都抑制
7. 还有个带阻滤波器，是带通的反。

OpenCV中使用傅里叶变换

如果有朋友想要快速上手在OpenCV中使用傅里叶变换，只需要记住

1. 傅立叶变换的物理意义是将图像的灰度分布函数变换为图像的频率分布函数、
2. 傅立叶变换提供另外一个角度来观察图像，可以将图像从灰度分布转化到频率分布上来观察图像的特征。
3. 对一张图像做傅里叶变换，就是将它分解为 sin 和 cos 两部分，也就是将图像从空间域转换到频域。
   

import numpy as np
import cv2
from matplotlib import pyplot as plt
# 导入一张灰度图
img = cv2.imread('lena.jpg',0)
# 将图像转换为float32的格式
img_float32 = np.float32(img)
# OpenCV的傅里叶变换函数，输出的是图像经过傅里叶变换后的结果
dft = cv2.dft(img_float32, flags = cv2.DFT_COMPLEX_OUTPUT)
# 此时，图像频谱中的零频率分量位于频谱图像（频域图像）的左上角，
# 通常使用 numpy.fft.fftshift() 来将零频率成分移动到频域图像的中心位置
dft_shift = np.fft.fftshift(dft)
# 我们得到的是一个复数数组，为了显示图像，需要将他们的值调到 [0,255] 的灰度空间中
magnitude_spectrum = 20*np.log(cv2.magnitude(dft_shift[:,:,0],dft_shift[:,:,1]))

plt.subplot(121),plt.imshow(img, cmap = 'gray')
plt.title('Input Image'), plt.xticks([]), plt.yticks([])
plt.subplot(122),plt.imshow(magnitude_spectrum, cmap = 'gray')
plt.title('Magnitude Spectrum'), plt.xticks([]), plt.yticks([])
plt.show()

右边的图是左边图的频谱图

那频谱图是什么呢？具体的解释大家可以看这篇文章：https://blog.csdn.net/u014488388/article/details/52612456?t=1496943343720&amp;utm_medium=distribute.pc_relevant.none–task–blog-2_defaultbaidujs_baidulandingword~default-0-52612456-blog-94553357.pc_relevant_3mothn_strategy_and_data_recovery&spm=1001.2101.3001.4242.1&utm_relevant_index=3

那简单的解释就是：
可以将频谱的中心看做坐标原点，横轴为x轴，纵轴是y轴，建立坐标系。
频谱平面上的坐标（X,Y）的黑白，表示图像是否含有z = sin(Xw + Yw)这个正弦平面波成分，白即是有含有。
但是最后的图是我们经过对数运算后的图，原本的图看起来不是很清晰，所以我们用对数运算将对比度放大了看的就比较清晰了

未经对数运算的频谱

高通滤波和低通滤波

刚才我们得到了这张图片的频谱图，那下面我们就要对这个频谱图进行操作

https://blog.csdn.net/weixin_51995147/article/details/124767050?utm_medium=distribute.pc_relevant.none–task–blog-2_defaultbaidujs_baidulandingword~default-0-124767050-blog-71699582.pc_relevant_landingrelevant&spm=1001.2101.3001.4242.1&utm_relevant_index=3

import numpy as np
import cv2
from matplotlib import pyplot as plt
# 导进一张图片
img = cv2.imread('lena.jpg',0)
# 转换为 float32的格式
img_float32 = np.float32(img)
# 傅里叶变换
dft = cv2.dft(img_float32, flags = cv2.DFT_COMPLEX_OUTPUT)
# 将低频移到中间
dft_shift = np.fft.fftshift(dft)
# 求图片的中心位置
rows, cols = img.shape
crow, ccol = int(rows/2) , int(cols/2)     # 中心位置

# 低通滤波：图像中心的是低频，我们想要保留低频，过滤高频，就用一个掩膜，中心的是1，其他是0
mask = np.zeros((rows, cols, 2), np.uint8)
mask[crow-30:crow+30, ccol-30:ccol+30] = 1

# IDFT：傅里叶的逆变换
# 用频谱图乘掩膜，那最后就中心的保留了，其他都是0
fshift = dft_shift*mask
# 将低频的再移到原来的位置
f_ishift = np.fft.ifftshift(fshift)
# 进行傅里叶的逆变换
img_back = cv2.idft(f_ishift)
# 将实部和虚部结合
img_back = cv2.magnitude(img_back[:,:,0],img_back[:,:,1])

plt.subplot(121),plt.imshow(img, cmap = 'gray')
plt.title('Input Image'), plt.xticks([]), plt.yticks([])
plt.subplot(122),plt.imshow(img_back, cmap = 'gray')
plt.title('Result'), plt.xticks([]), plt.yticks([])

plt.show()   

总结

那到本期，OpenCV有关的图像基本操作我们已经全部就介绍完了，但是只是草草地介绍这个一下的话，那对于学习本身是毫无意义的，所以接下来的一遍，我们将引入一个银行卡号图像检测的实战内容，帮助大家理解上述讲过的所有图像操作

我是Mayphry，从一点点到亿点点，我们下次再见

代码007普通

打赏 收藏 海报 链接