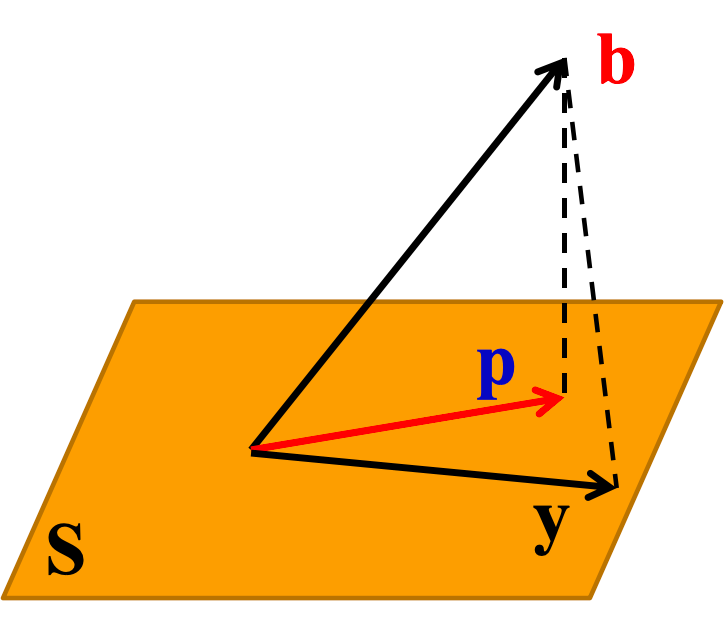
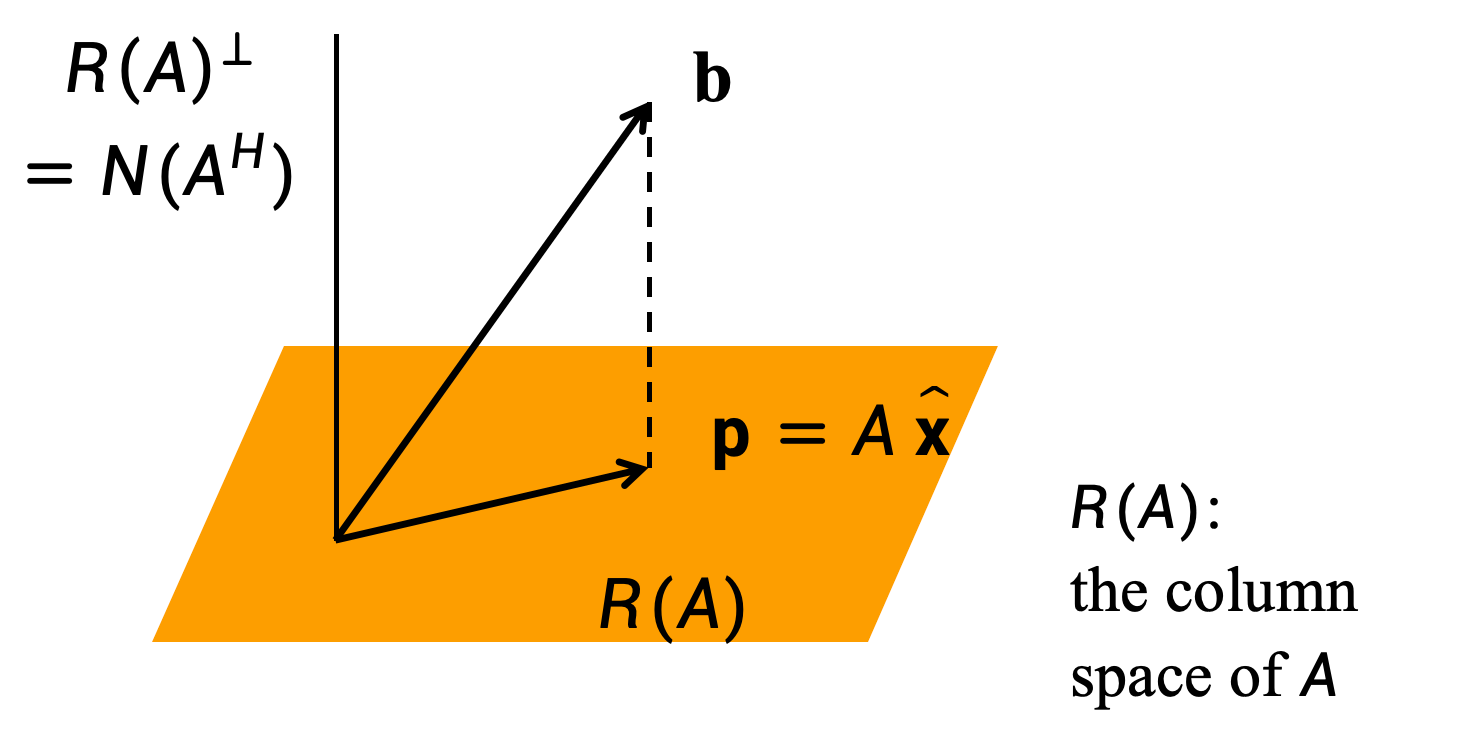
,长度为
1
1
1的称为单位向量。如果
≠
v
≠
0
vneq 0
v=0,则
u
u
u在
v
v
α
=
(
u
,
v
)
∣
∣
v
∣
∣
α=∣∣v∣∣(u,v),
u
u
u在
v
v
=
α
v
∣
∣
v
∣
∣
=
(
u
,
v
)
(
v
,
v
)
v
p=alphafrac{v}{||v||}=frac{(u,v)}{(v,v)}v
p=α∣∣v∣∣v=(v,v)(u,v)v
(
u
,
v
)
=
0
(u,v)=0
(u,v)=0,则称
u
u
u和
v
v
v正交
内积的基本性质
设
u
,
v
∈
V
u,vin V
u,v∈V,其中
V
V
V是内积空间,则
-
勾股定理:如果
u
⊥
v
u⊥v,则
∣
∣
u
−
v
∣
∣
2
=
∣
∣
u
∣
∣
2
+
∣
∣
v
∣
∣
2
||u-v||^2=||u||^2+||v||^2
∣∣u−v∣∣2=∣∣u∣∣2+∣∣v∣∣2
证明:
∣
∣
u
−
v
∣
∣
2
=
(
u
−
v
,
u
−
v
)
=
(
u
,
u
−
v
)
+
(
−
v
,
u
−
v
)
=
(
u
,
u
)
−
(
u
,
v
)
−
(
v
,
u
)
+
(
v
,
v
)
=
(
u
,
u
)
−
(
u
,
v
)
−
(
u
,
v
)
‾
+
(
v
,
v
)
||u-v||^2=(u-v,u-v)=(u,u-v)+(-v,u-v)\=(u,u)-(u,v)-(v,u)+(v,v)=(u,u)-(u,v)-overline{(u,v)}+(v,v)
∣∣u−v∣∣2=(u−v,u−v)=(u,u−v)+(−v,u−v)=(u,u)−(u,v)−(v,u)+(v,v)=(u,u)−(u,v)−(u,v)+(v,v)
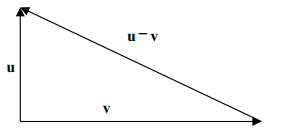
-
柯西不等式:
∣
(
u
,
v
)
∣
≤
∣
∣
u
∣
∣
∣
∣
v
∣
∣
∣(u,v)∣≤∣∣u∣∣ ∣∣v∣∣。等式成立当且仅当
u
u
u和
v
v
证明:
如果
u
,
v
u,v
u,v线性相关,则设
u
=
v
,
∈
F
u=kv,k∈F,则
(
u
,
v
)
=
(
k
v
,
v
)
=
k
∣
∣
v
∣
∣
2
(u,v)=(kv,v)=k||v||^2
(u,v)=(kv,v)=k∣∣v∣∣2
如果
u
,
v
u,v
u,v线性无关,设
z
=
u
−
(
u
,
v
)
(
v
,
v
)
v
z=u-frac{(u,v)}{(v,v)}v
z=u−(v,v)(u,v)v,则
(
z
,
v
)
=
(
u
−
(
u
,
v
)
(
v
,
v
)
v
,
v
)
=
(
u
,
v
)
−
(
u
,
v
)
(
v
,
v
)
(
v
,
v
)
=
0
(z,v)=(u-frac{(u,v)}{(v,v)}v,v)=(u,v)-frac{(u,v)}{(v,v)}(v,v)=0
(z,v)=(u−(v,v)(u,v)v,v)=(u,v)−(v,v)(u,v)(v,v)=0,则
z
z
z和
v
v
v正交。转换得到
u
=
z
+
(
u
,
v
)
(
v
,
v
)
v
u=z+frac{(u,v)}{(v,v)}v
u=z+(v,v)(u,v)v,根据正交性,结合勾股定理则
∣
∣
u
∣
∣
2
=
∣
∣
z
∣
∣
2
+
∣
(
u
,
v
)
(
v
,
v
)
∣
2
∣
∣
v
∣
∣
2
=
∣
∣
z
∣
∣
2
+
∣
(
u
,
v
)
∣
2
(
∣
∣
v
∣
∣
2
)
2
∣
∣
v
∣
∣
2
=
∣
∣
z
∣
∣
2
+
∣
(
u
,
v
)
∣
2
∣
∣
v
∣
∣
2
||u||^2=||z||^2+|frac{(u,v)}{(v,v)}|^2||v||^2=||z||^2+frac{|(u,v)|^2}{(||v||^2)^2}||v||^2=||z||^2+frac{|(u,v)|^2}{||v||^2}
∣∣u∣∣2=∣∣z∣∣2+∣(v,v)(u,v)∣2∣∣v∣∣2=∣∣z∣∣2+(∣∣v∣∣2)2∣(u,v)∣2∣∣v∣∣2=∣∣z∣∣2+∣∣v∣∣2∣(u,v)∣2
又因为
∣
∣
z
∣
∣
2
0
∣
∣
z
∣
∣
2
||z||^2
∣∣z∣∣2必大于
0
0
0),则
∣
(
u
,
v
∣
<
∣
∣
u
∣
∣
∣
∣
v
∣
∣
∣(u,v∣<∣∣u∣∣ ∣∣v∣∣
-
三角不等式:
∣
∣
u
+
v
∣
∣
2
≤
∣
∣
u
∣
∣
2
+
∣
∣
v
∣
∣
2
||u+v||^2leq ||u||^2+||v||^2
∣∣u+v∣∣2≤∣∣u∣∣2+∣∣v∣∣2
证明:
∣
∣
u
+
v
∣
∣
2
=
(
u
+
v
,
u
+
v
)
=
(
u
,
u
+
v
)
+
(
v
,
u
+
v
)
=
(
u
,
u
)
+
(
u
,
v
)
+
(
v
,
u
)
+
(
v
,
v
)
=
(
u
,
u
)
+
(
u
,
v
)
+
(
u
,
v
)
‾
+
(
v
,
v
)
≤
∣
∣
u
∣
∣
2
+
2
∣
(
u
,
v
)
∣
+
∣
∣
v
∣
∣
2
≤
∣
∣
u
∣
∣
2
+
2
∣
∣
u
∣
∣
∣
∣
v
∣
∣
+
∣
∣
v
∣
∣
2
=
(
∣
∣
u
∣
∣
+
∣
∣
v
∣
∣
)
2
||u+v||^2=(u+v,u+v)=(u,u+v)+(v,u+v)\=(u,u)+(u,v)+(v,u)+(v,v)=(u,u)+(u,v)+overline{(u,v)}+(v,v)\ leq ||u||^2+2|(u,v)|+||v||^2 leq ||u||^2+2||u||space ||v||+||v||^2=(||u||+||v||)^2
∣∣u+v∣∣2=(u+v,u+v)=(u,u+v)+(v,u+v)=(u,u)+(u,v)+(v,u)+(v,v)=(u,u)+(u,v)+(u,v)+(v,v)≤∣∣u∣∣2+2∣(u,v)∣+∣∣v∣∣2≤∣∣u∣∣2+2∣∣u∣∣ ∣∣v∣∣+∣∣v∣∣2=(∣∣u∣∣+∣∣v∣∣)2
-
平行四边形准则:
∣
∣
u
+
v
∣
∣
2
+
∣
∣
u
−
v
∣
∣
2
=
2
(
∣
∣
u
∣
∣
2
+
∣
∣
v
∣
∣
2
)
||u+v||^2+||u-v||^2=2(||u||^2+||v||^2)
∣∣u+v∣∣2+∣∣u−v∣∣2=2(∣∣u∣∣2+∣∣v∣∣2)
证明:
∣
∣
u
−
v
∣
∣
2
=
(
u
−
v
,
u
−
v
)
=
(
u
,
u
−
v
)
+
(
−
v
,
u
−
v
)
=
(
u
,
u
)
−
(
u
,
v
)
−
(
v
,
u
)
+
(
v
,
v
)
=
(
u
,
u
)
−
(
u
,
v
)
−
(
u
,
v
)
‾
+
(
v
,
v
)
∣
∣
u
+
v
∣
∣
2
=
(
u
+
v
,
u
+
v
)
=
(
u
,
u
+
v
)
+
(
v
,
u
+
v
)
=
(
u
,
u
)
+
(
u
,
v
)
+
(
v
,
u
)
+
(
v
,
v
)
=
(
u
,
u
)
+
(
u
,
v
)
+
(
u
,
v
)
‾
+
(
v
,
v
)
∣
∣
u
+
v
∣
∣
2
+
∣
∣
u
−
v
∣
∣
2
=
2
(
u
,
u
)
+
2
(
v
,
v
)
=
2
(
∣
∣
u
∣
∣
2
+
∣
∣
v
∣
∣
2
)
||u-v||^2=(u-v,u-v)=(u,u-v)+(-v,u-v)\=(u,u)-(u,v)-(v,u)+(v,v)=(u,u)-(u,v)-overline{(u,v)}+(v,v)\ ||u+v||^2=(u+v,u+v)=(u,u+v)+(v,u+v)\=(u,u)+(u,v)+(v,u)+(v,v)=(u,u)+(u,v)+overline{(u,v)}+(v,v)\ ||u+v||^2+||u-v||^2=2(u,u)+2(v,v)=2(||u||^2+||v||^2)
∣∣u−v∣∣2=(u−v,u−v)=(u,u−v)+(−v,u−v)=(u,u)−(u,v)−(v,u)+(v,v)=(u,u)−(u,v)−(u,v)+(v,v)∣∣u+v∣∣2=(u+v,u+v)=(u,u+v)+(v,u+v)=(u,u)+(u,v)+(v,u)+(v,v)=(u,u)+(u,v)+(u,v)+(v,v)∣∣u+v∣∣2+∣∣u−v∣∣2=2(u,u)+2(v,v)=2(∣∣u∣∣2+∣∣v∣∣2)