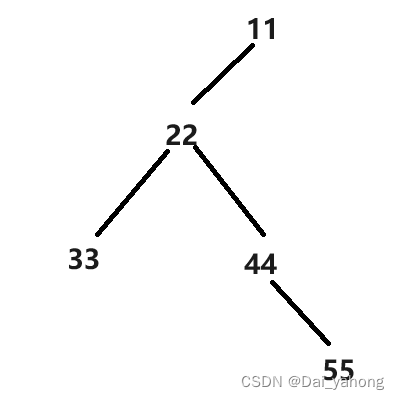
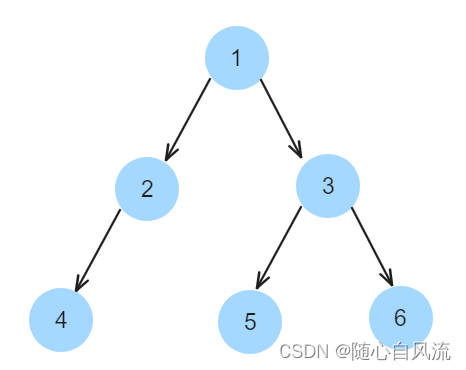
1 概念
2 分类
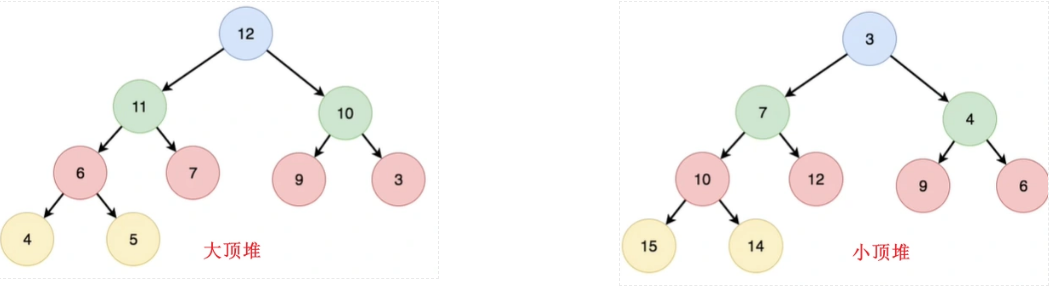
3 建堆方法
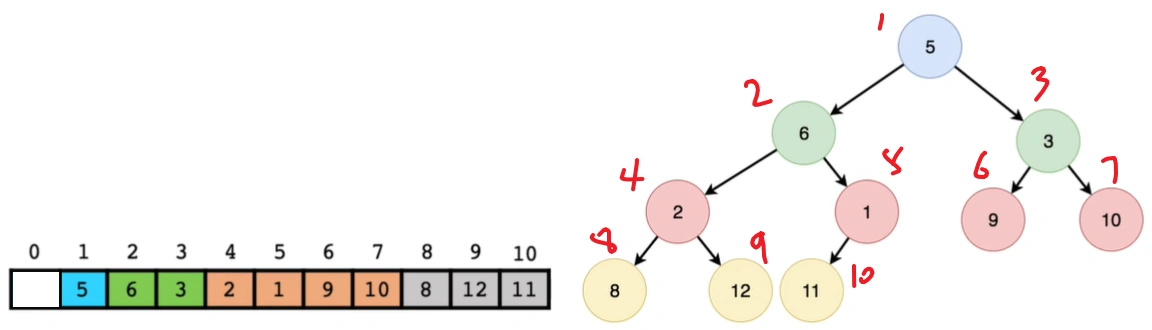
3.1 堆尾插入元素建堆法(自顶向下)
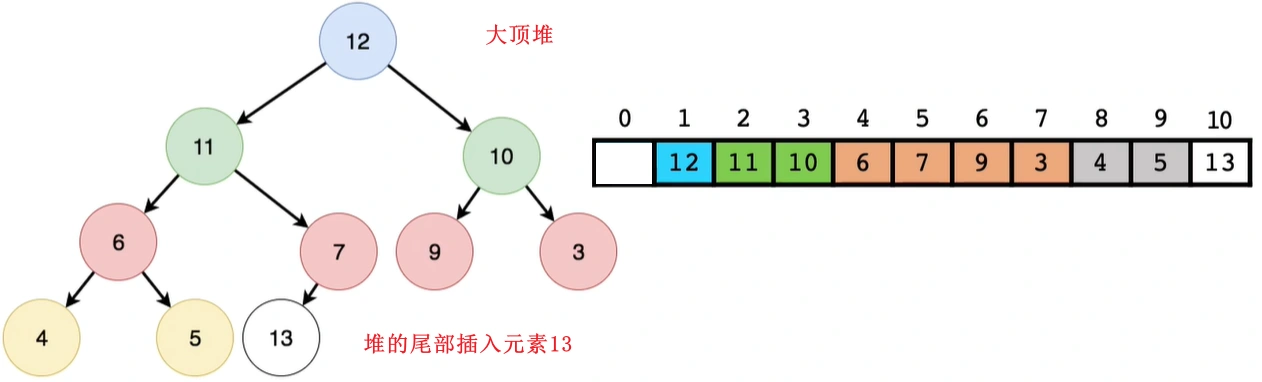
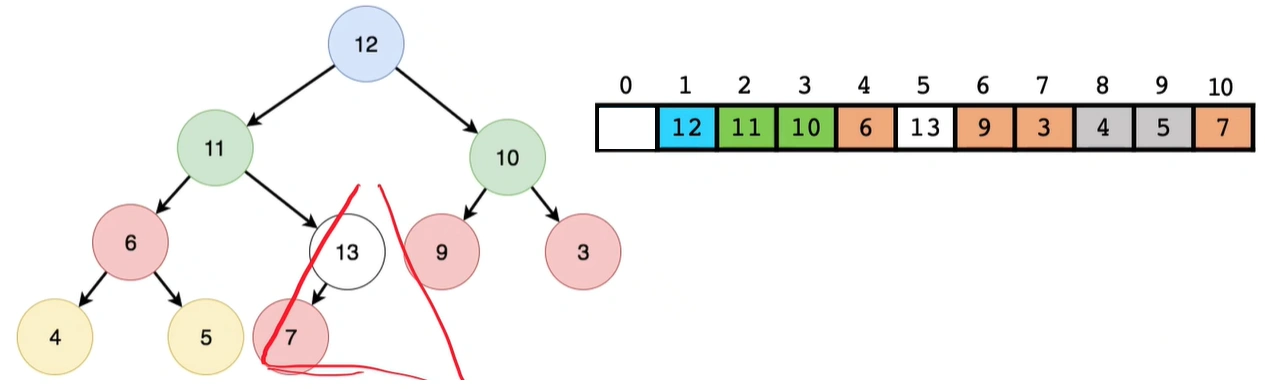
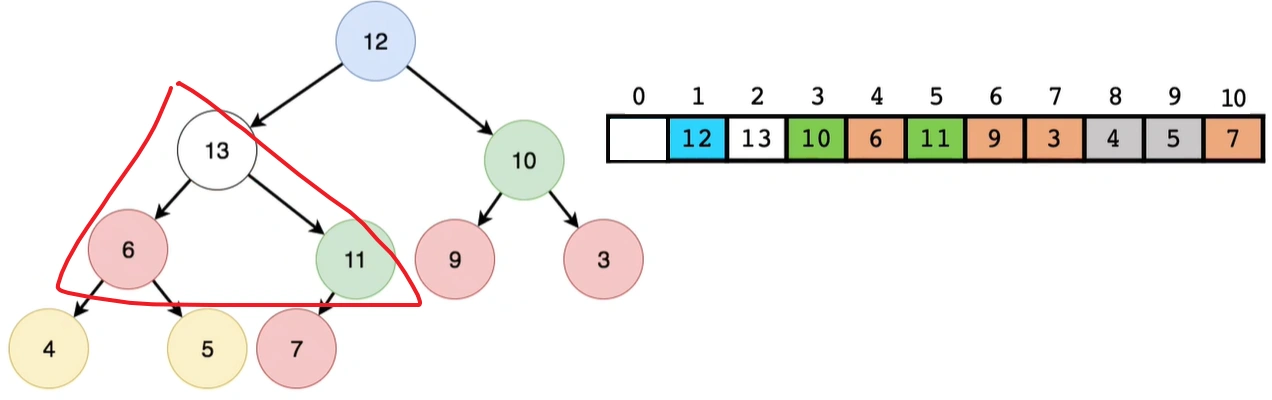
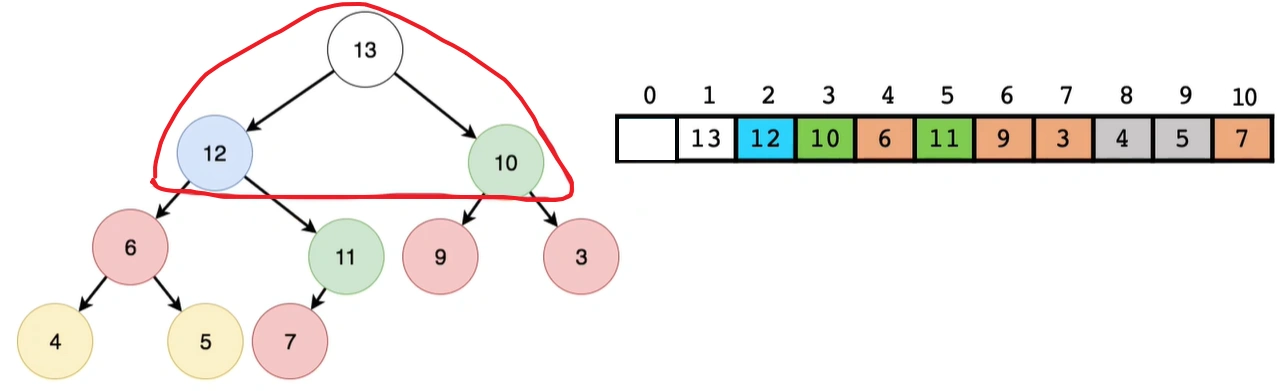
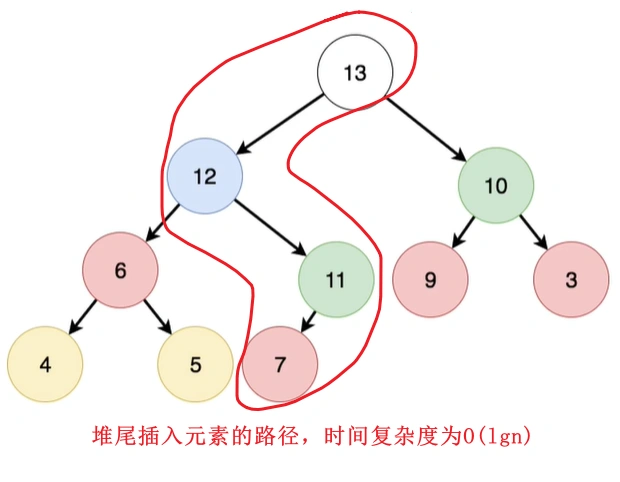
3.2 线性建堆法(自下向上的)
3.3 两种建堆方法的时间复杂度分析
- 树的高度与节点关系为:
sn=h∑N=12(N−1)=20+21+22+…+2(h−2)+2(h−1)=2h−1,N∈[1,h]��=∑�=1ℎ2(�−1)=20+21+22+…+2(ℎ−2)+2(ℎ−1)=2ℎ−1,�∈[1,ℎ]
3.3.1 插入建堆法的时间复杂度分析– o(n*logn)
T=(N−1)∗2(N−1)+(N−2)∗2(N−2)+(N−3)∗2(N−3)+….+1∗21+0∗20�=(�−1)∗2(�−1)+(�−2)∗2(�−2)+(�−3)∗2(�−3)+….+1∗21+0∗20
T′=2∗T=(N−1)∗2N+(N−2)∗2(N−1)+(N−3)∗2(N−2)+….+1∗22+0∗21�′=2∗�=(�−1)∗2�+(�−2)∗2(�−1)+(�−3)∗2(�−2)+….+1∗22+0∗21
T=T′−T=(N−1)∗2N−(2(N−1)+2(N−2)+….+22+21)=(N−1)∗2N+(2−2N)=N∗2N+2(N+1)+2�=�′−�=(�−1)∗2�−(2(�−1)+2(�−2)+….+22+21)=(�−1)∗2�+(2−2�)=�∗2�+2(�+1)+2
o(T)=o(h∗2h−2(h+1)+2)≈o(h∗2h)=o((sn+1)∗log2(sn+1))=o(nlog2n)�(�)=�(ℎ∗2ℎ−2(ℎ+1)+2)≈�(ℎ∗2ℎ)=�((��+1)∗���2(��+1))=�(����2�)
3.3.2 线性建堆法的时间复杂度分析:- o(n)
T=0∗2(N−1)+1∗2(N−2)+2∗2(N−3)+….+(N−2)∗21+(N−1)∗20�=0∗2(�−1)+1∗2(�−2)+2∗2(�−3)+….+(�−2)∗21+(�−1)∗20
T′=2∗T=1∗2(N−1)+2∗2(N−2)+….+(N−2)∗22+(N−1)∗21�′=2∗�=1∗2(�−1)+2∗2(�−2)+….+(�−2)∗22+(�−1)∗21
T=T′−T=2(N−1)+2(N−2)+….+22+21−(N−1)∗20=2N−N−1�=�′−�=2(�−1)+2(�−2)+….+22+21−(�−1)∗20=2�−�−1
o(T)=o(2h−h−1)≈o(2h)=o(sn+1)=o(n)�(�)=�(2ℎ−ℎ−1)≈�(2ℎ)=�(��+1)=�(�)
4 删除堆顶元素- o(logn)
- 删除步骤:
- 删除堆顶元素的示意图:
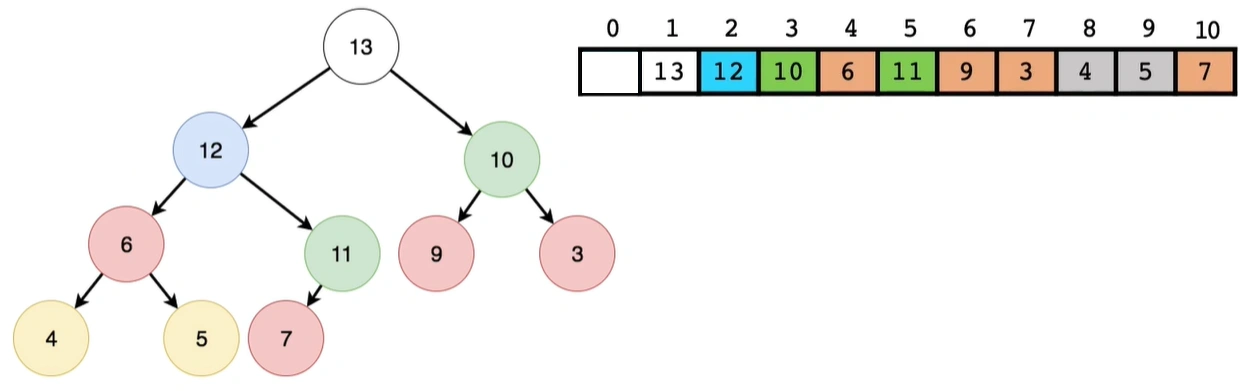
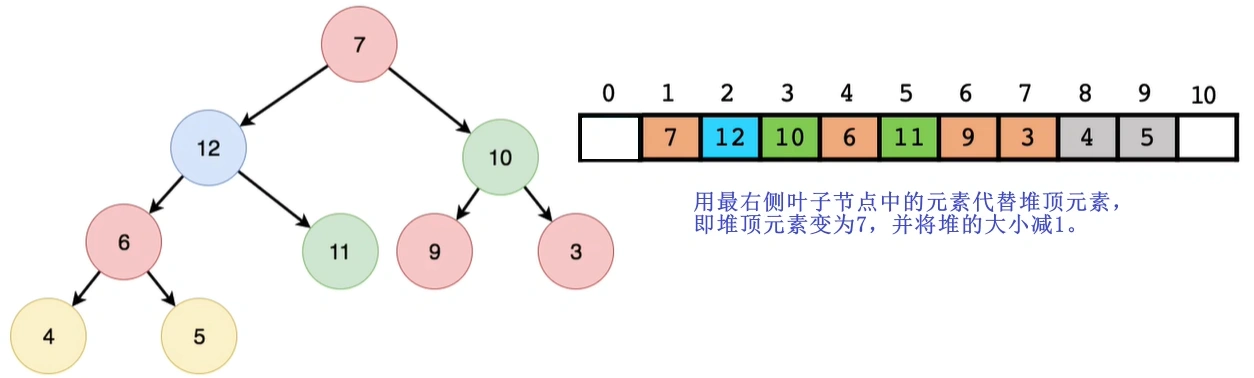
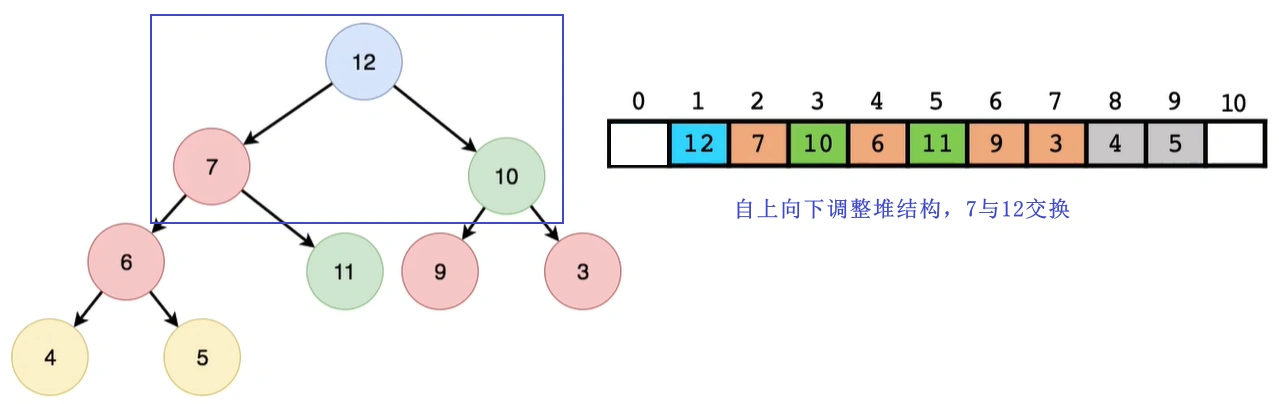
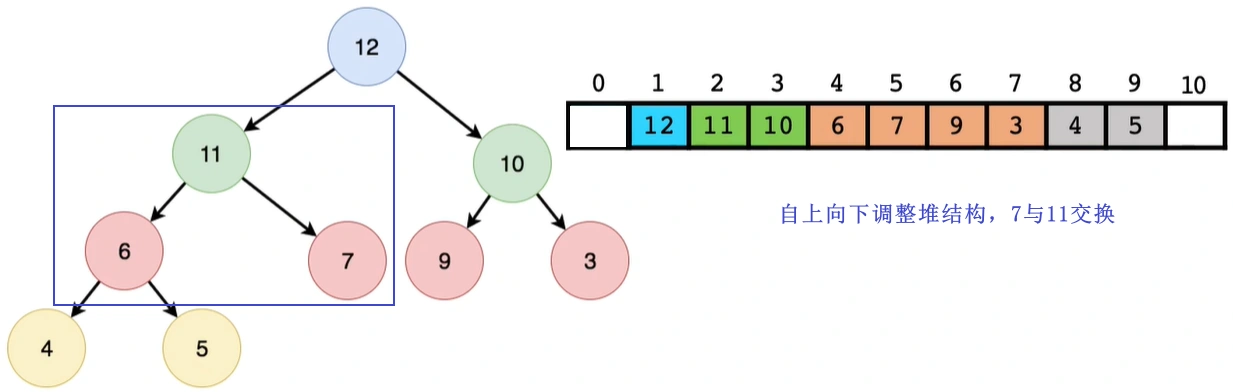
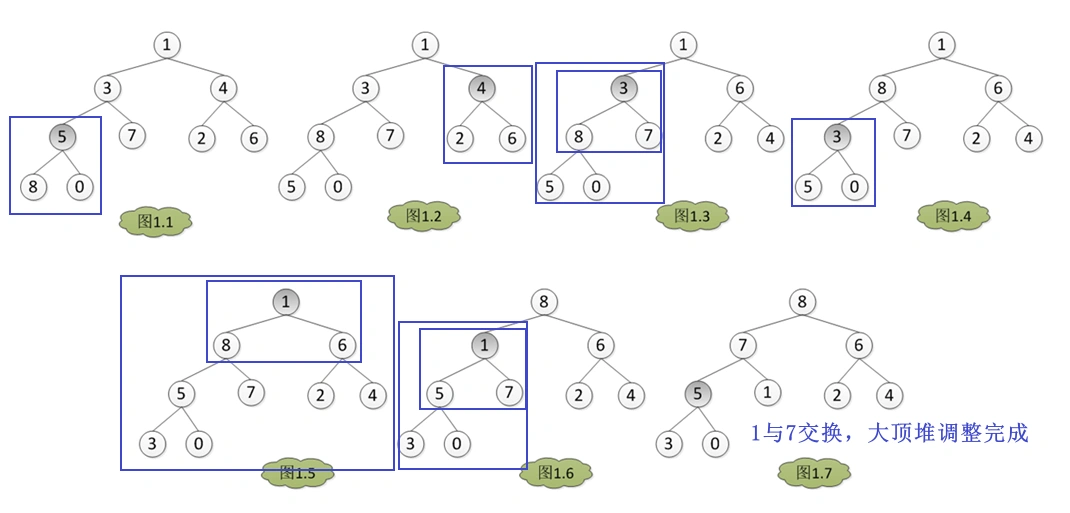
5 堆排序 – o(n*logn)
6 代码演示
6.1 插入建堆法
#include <stdio.h>
#include <time.h>
#include <stdlib.h>
#define SWAP(a, b) {
__typeof(a) __temp = a; a = b; b = __temp;
}
typedef struct priority_queue {
int *data;
int cnt, size; // cnt:堆中的元素个数,size:堆空间的容量
} priority_queue;
priority_queue* init(int size) {
priority_queue* q = (priority_queue*)malloc(sizeof(priority_queue));
// 多申请1个空间,是因为堆顶元素的编号为1,这样在建堆过程中可以减少1次加法运算
q->data = (int*)malloc((size + 1) * sizeof(int));
q->cnt = 0;
q->size = size;
return q;
}
int empty(priority_queue* q) {
return q->cnt == 0;
}
// 获取堆顶元素
int top(priority_queue* q) {
return q->data[1];
}
// 堆尾插入元素
int push(priority_queue* q, int v) {
if (q == NULL) return 0;
if (q->cnt == q->size) return 0;
// 将元素插入堆尾
q->data[++(q->cnt)] = v;
// 重新调整堆结构(大顶堆)--- 自下向上
int ind = q->cnt; // 获取当前元素的编号
while (ind >> 1 && q->data[ind] > q->data[ind >> 1]) {
SWAP(q->data[ind], q->data[ind >> 1]);
ind = ind >> 1;
}
return 1;
}
// 删除堆顶元素
int pop(priority_queue* q) {
if (q == NULL) return 0;
if (q->cnt == 0) return 0;
// 将堆尾元素赋值堆顶
q->data[1] = q->data[(q->cnt)--];
// 重新调整堆结构(大顶堆)--- 自上向下
int ind = 1; // 堆顶元素的编号
while ((ind << 1) <= q->cnt) {
int temp = ind, lnode = ind << 1, rnode = ind << 1 | 1;
if (q->data[temp] < q->data[lnode]) temp = lnode;
if (rnode <= q->cnt && q->data[temp] < q->data[rnode]) temp = rnode;
if (temp == ind) break; // 当前三元组结构未发生变化
SWAP(q->data[temp], q->data[ind]);
ind = temp;
}
return 1;
}
void clear(priority_queue* q) {
if (q == NULL) return ;
if (q->data) free(q->data);
free(q);
}
int main() {
srand(time(0));
const int N = 10;
priority_queue* q = init(N);
for (int i = 1; i <= N; i++) {
int v = rand() % 100;
push(q, v);
}
for (int i = 1; i <= q->cnt; i++) {
printf("%d ", q->data[i]);
}
printf("n");
while (!empty(q)) {
printf("%d ", top(q));
pop(q);
}
printf("n");
clear(q);
return 0;
}
6.2 堆排序(线性建堆法)
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
// 线性建堆法:建堆时间 o(n)
// 堆排序:建堆时间 + 堆排序时间 = o(n) + o(n*lgn) = o(n*lgn)
#define SWAP(a, b) {
__typeof(a) __temp = a; a = b; b = __temp;
}
// 根节点:i,左子树节点:2*i,右子树节点:2*i+1,i >= 1;
// arr:输入数组,n:数组元素的个数,ind:代表完全二叉树的节点编号
void downUpdate(int *arr, int n, int ind) {
// ind << 1:下一层节点编号,即当前节点的左子树节点编号,其节点编号代表元素的个数
while ((ind << 1) <= n) {
int temp = ind, l = ind << 1, r = ind << 1 | 1; // l:下一层的左子树节点编号,r:下一层的右子树节点编号
// 大顶堆构建(堆排序:从小到大排序),任意三元组的父节点为极大值
if (arr[l] > arr[temp]) temp = l;
if (r <= n && arr[r] > arr[temp]) temp = r;
// 小顶堆构建(堆排序:从大到小排序),任意三元组的父节点为极小值
// if (arr[l] < arr[temp]) temp = l;
// if (r <= n && arr[r] < arr[temp]) temp = r;
if (ind == temp) break; // ind == temp:三元组中的父节点为极大(小)值节点
swap(arr[temp], arr[ind]);
ind = temp;
}
return ;
}
// arr:待排序的数组,n:数组元素的个数
void heap_sort(int *arr, int n) {
// 待排序的数组索引从0开始编号,而堆结构采取从1开始编号,故需要arr -= 1
arr -= 1;
// 线性建堆法 -- o(n)
for (int i = n >> 1; i >= 1; i--) {
downUpdate(arr, n, i);
}
// 堆排序的步骤:
// 1. 将堆顶元素与堆尾元素交换
// 2. 对前n-1元素重新建堆
// 3. 重复1、2 两个过程,直到堆中的元素为1时停止
for (int i = n; i > 1; i--) { // o(n * lgn)
swap(arr[i], arr[1]);
downUpdate(arr, i - 1, 1);
}
return ;
}
void output(int *arr, int n) {
printf("[");
for (int i = 0; i < n; i++) {
i && printf(" ");
printf("%d", arr[i]);
}
printf("]n");
return ;
}
int main() {
srand(time(0));
#define MAX_N 10
int arr[MAX_N] = {0};
for (int i = 0; i < MAX_N; i++) {
arr[i] = rand() % 100;
}
output(arr, MAX_N);
heap_sort(arr, MAX_N);
output(arr, MAX_N);
#undef MAX_N
return 0;
}
原文地址:https://blog.csdn.net/softshow1026/article/details/134742874
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。
如若转载,请注明出处:http://www.7code.cn/show_24678.html
如若内容造成侵权/违法违规/事实不符,请联系代码007邮箱:suwngjj01@126.com进行投诉反馈,一经查实,立即删除!