人工智能|机器学习——感知器算法原理与python实现

感知器算法是一种可以直接得到线性判别函数的线性分类方法，它是基于样本线性可分的要求下使用的。

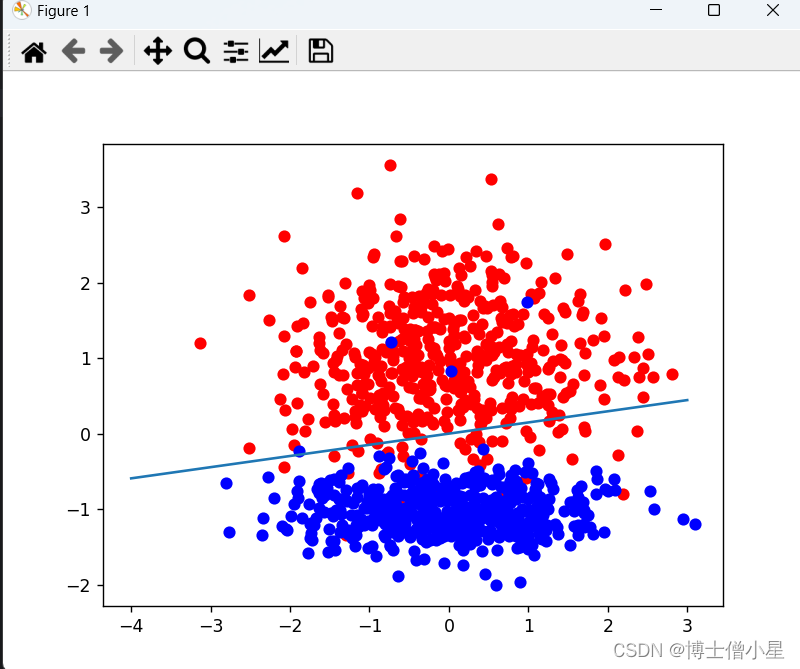
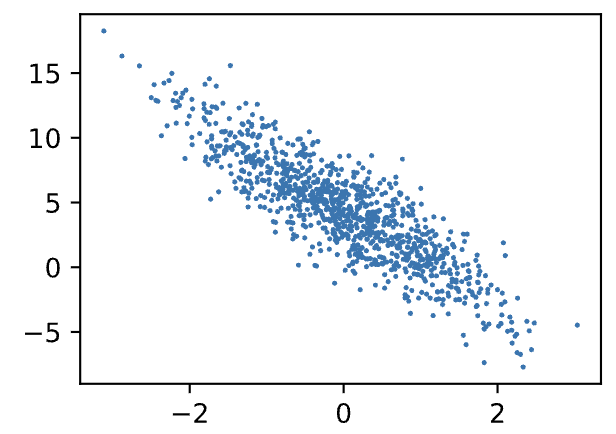
一、线性可分与线性不可分

为了方便讨论，我们蒋样本 $_{X}$ 增加了以为常数，得到增广样向量 y=（1; $x_{1}$ ; $x_{2}$ ;…; $x_{n}$ ）,则n个样本的集合为（ $y_{1}$ , $y_{2}$ ; $y_{3}$ ,….., $y_{n}$ ）,增广权矢量表示为 a = （ $omega _{0}$ ； $omega _{1}$ ; $omega _{2}$ …., $omega _{d}$ ）,我们得到新的怕没别函数

二、算法 步骤

三、算法 实现

1.生成 数据

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
 
# 加载数据集
iris = datasets.load_iris()
 
# 提取特征和目标变量
x = iris.data
y = iris.target
 
# 只选择两个特征变量和两个目标类别，进行简单的二分类
x = x[y &lt; 2, :2]
y = y[y &lt; 2]
 
# 绘制散点图
plt.scatter(x[y == 0, 0], x[y == 0, 1])  # 绘制类别0的样本
plt.scatter(x[y == 1, 0], x[y == 1, 1])  # 绘制类别1的样本
plt.show()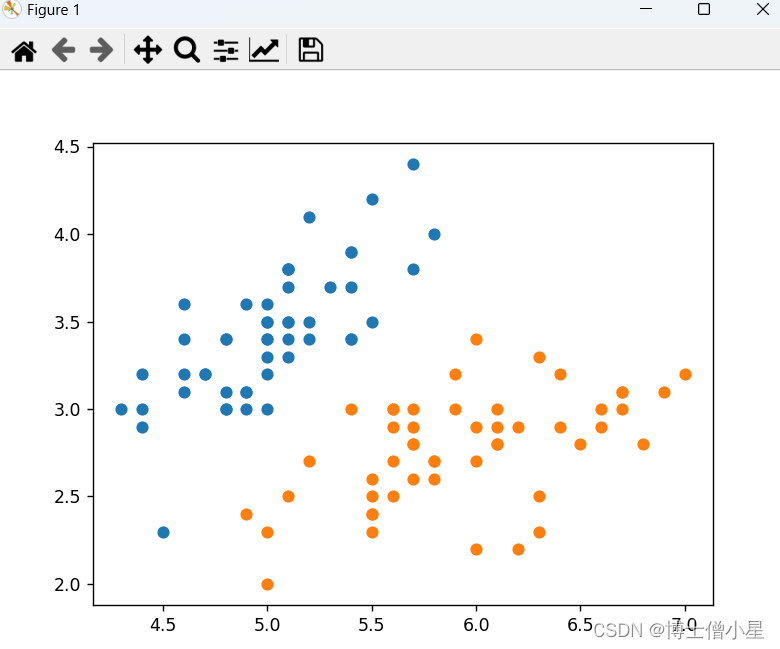

2.实现算法

def check(w, x, y):
    # 检查预测结果是否与真实标签一致
    return ((w.dot(x.T)&gt;0).astype(int)==y).all() 
 
def train(w, train_x, train_y, learn=1, max_iter=200):
    iter = 0
    while ~check(w, train_x, train_y) and iter<=max_iter:
        iter += 1
        for i in range(train_y.size):
            predict_y = (w.dot(train_x[i].T)&gt;0).astype(int)
            if predict_y != train_y[i]:
                # 根据预测和真实标签的差异调整权重
                w += learn*(train_y[i] - predict_y)*train_x[i]
    return w
 
def normalize(x):
    # 归一化函数，将输入数据转换到0-1范围
    max_x = np.max(x, axis=0)
    min_x = np.min(x, axis=0)
    norm_x = (max_x - x) / (max_x - min_x)
    return norm_x
 
norm_x = normalize(x)
train_x = np.insert(norm_x, 0, values=np.ones(100).T, axis=1)
w = np.random.random(3)
w = train(w, train_x, y)

3.绘制决策边界

def plot_decision_boundary(w, axis):
    # 生成决策边界的坐标网格
    x0, x1 = np.meshgrid(np.linspace(axis[0], axis[1], int((axis[1] - axis[0])*100)).reshape(1, -1),
                         np.linspace(axis[2], axis[3], int((axis[3] - axis[2])*100)).reshape(1, -1))
    x_new = np.c_[x0.ravel(), x1.ravel()]
    x_new = np.insert(x_new, 0, np.ones(x_new.shape[0]), axis=1)
    # 对网格中的点进行预测
    y_predict = (w.dot(x_new.T)&gt;0).astype(int)
    zz = y_predict.reshape(x0.shape)
 
    # 设置自定义的颜色映射
    from matplotlib.colors import ListedColormap
    custom_cmap = ListedColormap(['#EF9A9A', '#FFF59D', '#90CAF9'])
 
    # 绘制决策边界
    plt.contourf(x0, x1, zz, linewidth=5, cmap=custom_cmap)
 
# 绘制决策边界
plot_decision_boundary(w, axis=[-1, 1, -1, 1])
# 绘制类别为0的样本点（红色）
plt.scatter(norm_x[y==0, 0], norm_x[y==0, 1], color='red')
# 绘制类别为1的样本点（蓝色）
plt.scatter(norm_x[y==1, 0], norm_x[y==1, 1], color='blue')
# 显示图形
plt.show()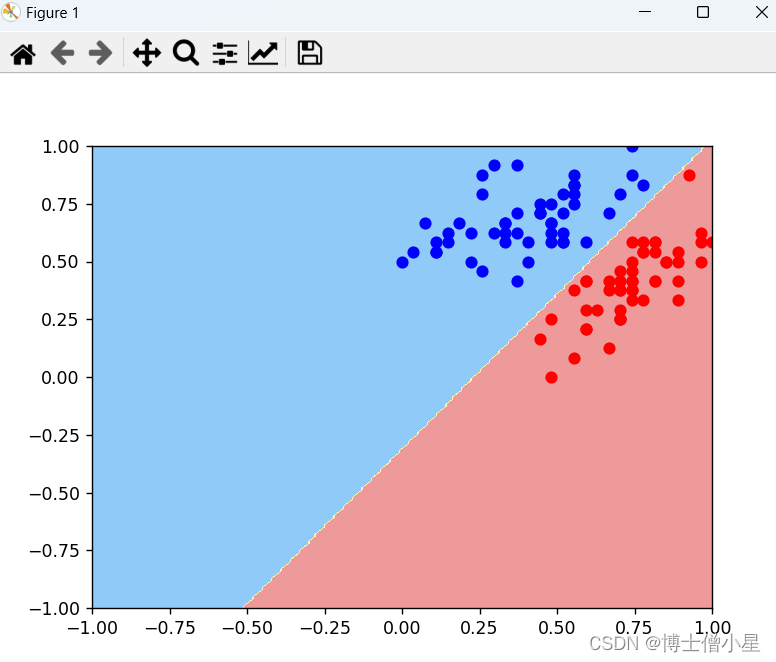

4.使用 sklearn库完成算法

from sklearn.datasets import make_classification
 
x,y = make_classification(n_samples=1000, n_features=2,n_redundant=0,n_informative=1,n_clusters_per_class=1)
 
#n_samples:生成样本的数量
 
#n_features=2:生成样本的特征数，特征数=n_informative（） + n_redundant + n_repeated
 
#n_informative：多信息特征的个数
 
#n_redundant：冗余信息，informative特征的随机线性组合
 
#n_clusters_per_class ：某一个类别是由几个cluster构成的 
 
#训练数据和测试数据
x_data_train = x[:800,:]
x_data_test = x[800:,:]
y_data_train = y[:800]
y_data_test = y[800:]
 
#正例和反例
positive_x1 = [x[i,0] for i in range(1000) if y[i] == 1]
positive_x2 = [x[i,1] for i in range(1000) if y[i] == 1]
negetive_x1 = [x[i,0] for i in range(1000) if y[i] == 0]
negetive_x2 = [x[i,1] for i in range(1000) if y[i] == 0]
from sklearn.linear_model import Perceptron
#定义感知机
clf = Perceptron(fit_intercept=False,shuffle=False)
#使用训练数据进行训练
clf.fit(x_data_train,y_data_train)
#得到训练结果，权重矩阵
print(clf.coef_)
#输出为：[[-0.38478876,4.41537463]]
 
#超平面的截距，此处输出为：[0.]
print(clf.intercept_)
 
#利用测试数据进行验证
acc = clf.score(x_data_test,y_data_test)
print(acc)
#得到的输出结果为0.98，这个结果还不错吧。
from matplotlib import pyplot as plt
#画出正例和反例的散点图
plt.scatter(positive_x1,positive_x2,c='red')
plt.scatter(negetive_x1,negetive_x2,c='blue')
#画出超平面（在本例中即是一条直线）
line_x = np.arange(-4,4)
line_y = line_x * (-clf.coef_[0][0] / clf.coef_[0][1]) - clf.intercept_
plt.plot(line_x,line_y)
plt.show()

四、优缺点

1.优点：

简单且易于实现：感知器算法是一种简单而有效的分类算法，它的基本原理易于理解，实现也相对简单。
收敛性保证：如果数据集是线性可分的，感知器算法可以收敛到最优解，即找到将不同类别分开的最优超平面。
适用于大型数据集：感知器算法具有较好的可扩展性，对于大型数据集也能够有效处理。

2缺点：

仅适用于线性可分问题：感知器算法只能处理线性可分的问题，当数据集不满足线性可分条件时，算法不能收敛到最优解。
对初始权重敏感：感知器算法的收敛性与初始权重的选择有关，较差的初始权重选择可能导致算法无法收敛或者收敛到较差的分类结果。
无法处理非线性问题：感知器算法无法处理非线性的分类问题，对于非线性数据集，需要使用更复杂的分类算法或者考虑使用特征转换等技术。
只能进行二分类：感知器算法只能进行二分类，无法直接处理多分类问题，需要通过拓展或组合多个感知器来处理多分类任务。