一. 无符号整数的表示和运算
无符号整数,即“自然数”,0、1、2、3、4…
比如这个通用寄存器只能存8位, 每次只能进行8位二进制数的运算

Tips:现在的个人计算机机器字长通常是64位,或至少32位 (也就是说一次能进行64或32位二进制的计算)
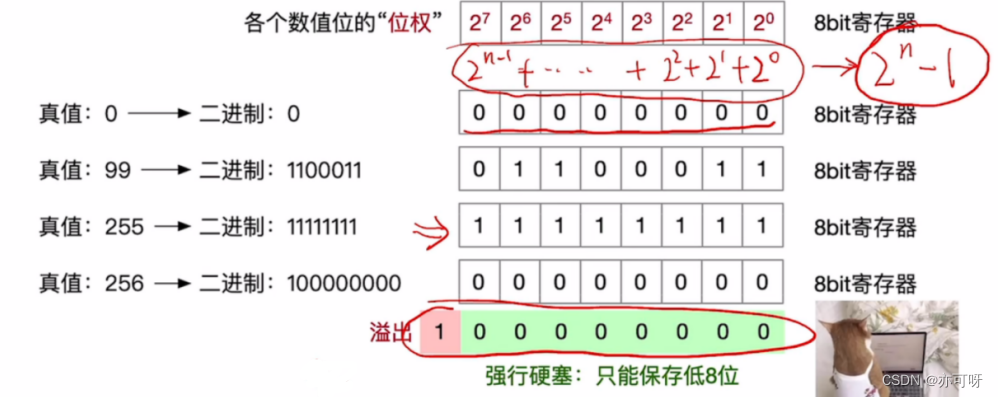
比如8位通用寄存器这就是存(00000000~11111111), 在多1位就会产生进位, 对于这个寄存器来讲就会溢出, 只能保存低位的8位
无符号整数:
1.1 无符号整数的减法运算
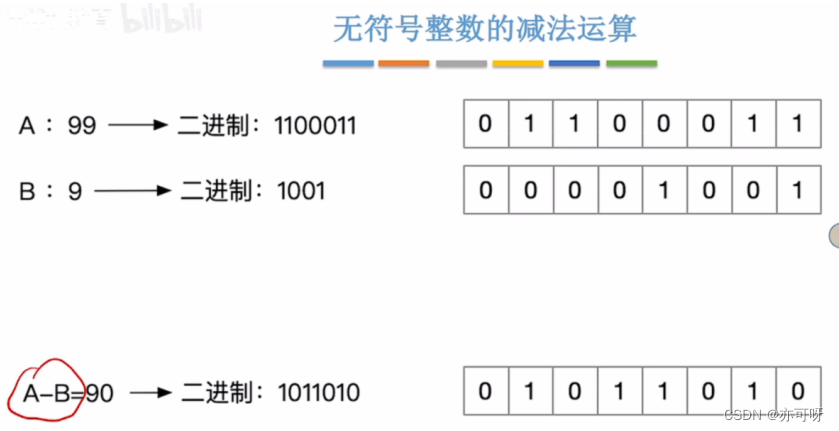
Tips: 加法电路造价便宜,减法电路造价昂贵, 若可将减法转变为加法,省钱!
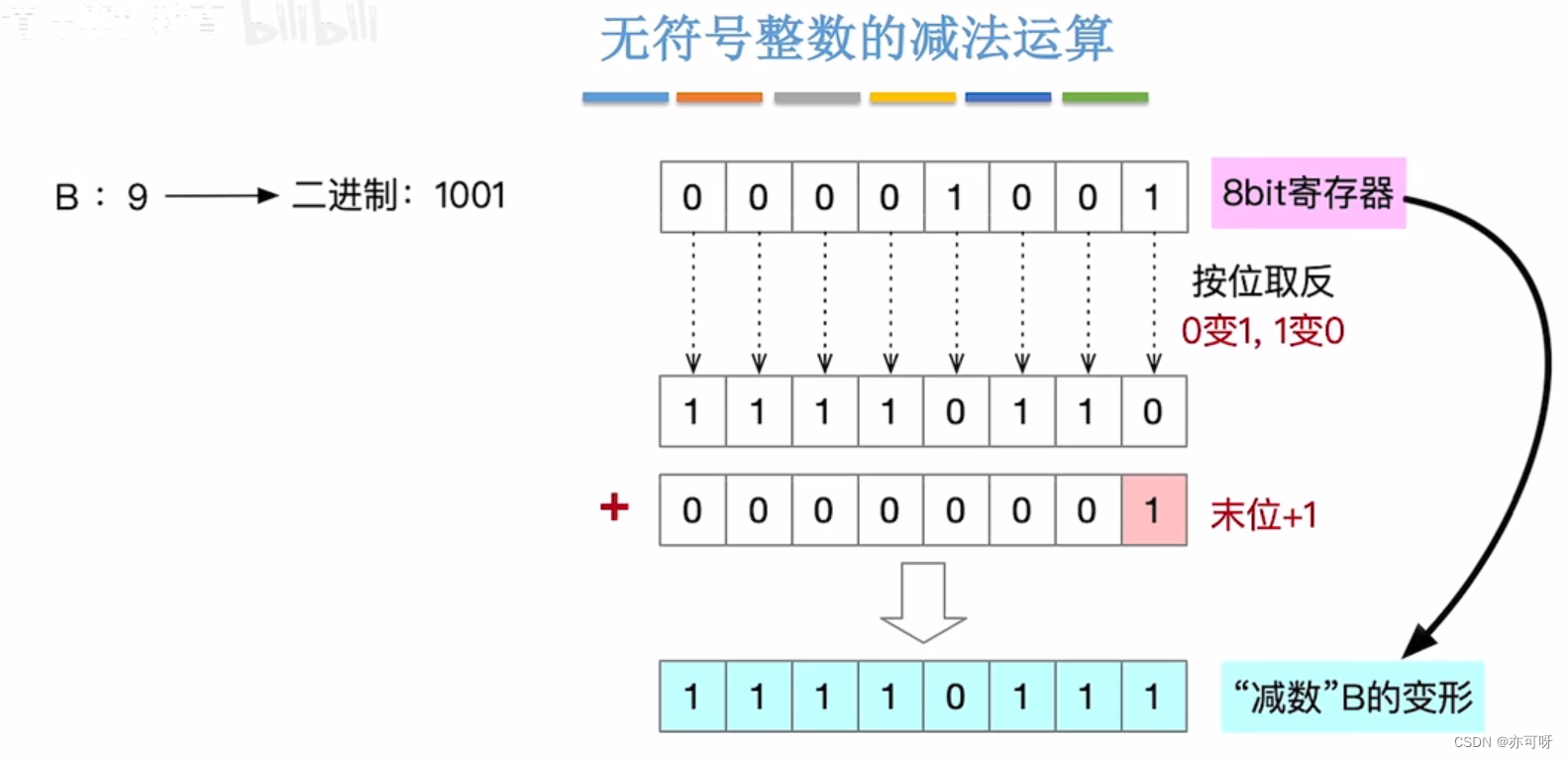
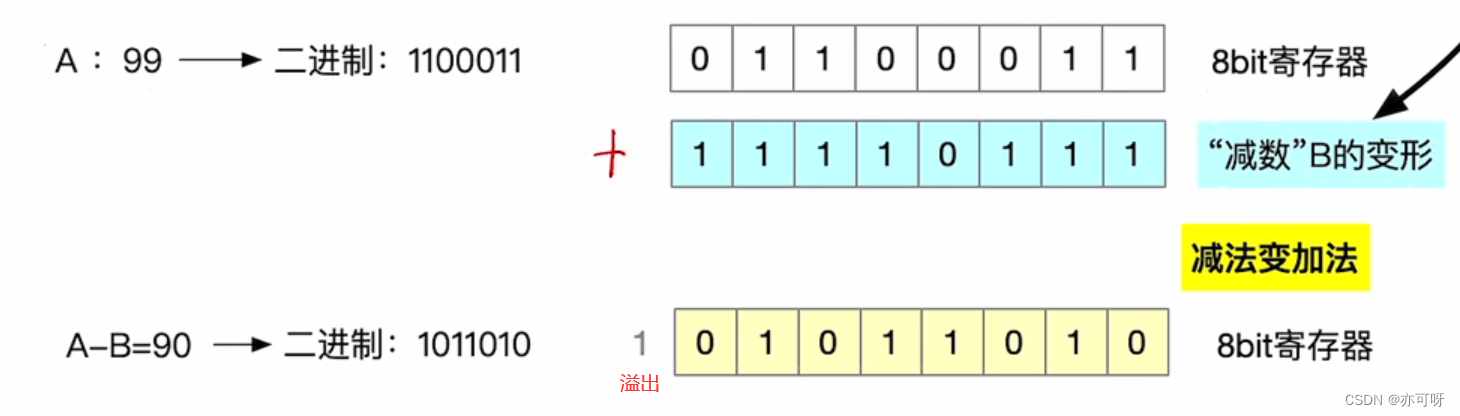
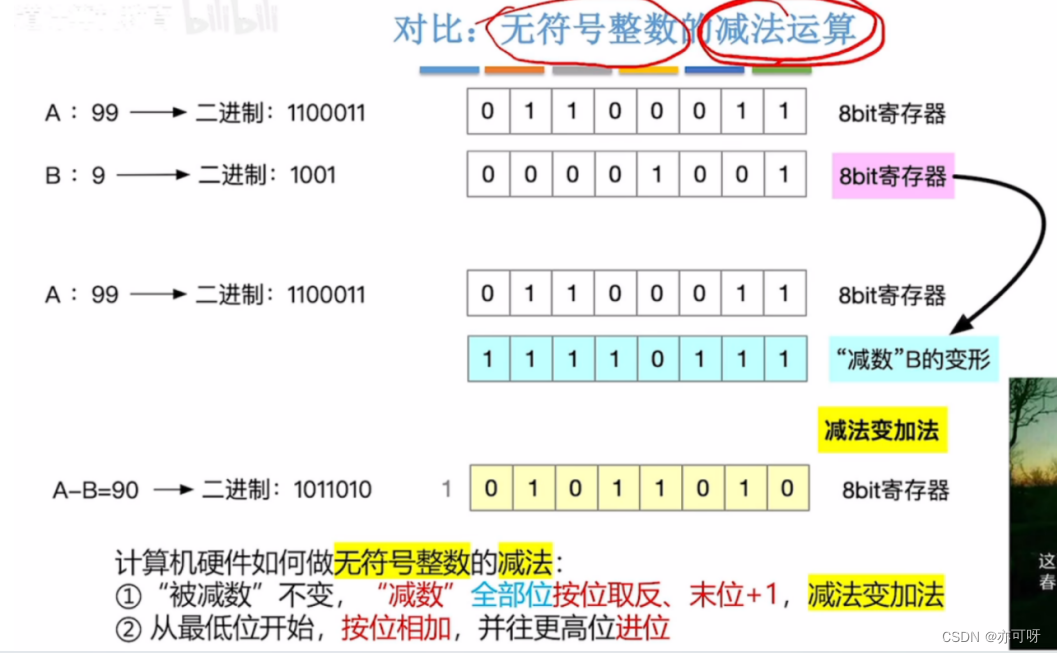
“被减数”不变,减数”全部位按位取反、末位+1,减法变加法从最低位开始,按位相加,并往更高位进位(这里我们只需要记住是这么做的就可以了, 如果要搞清楚就需要结合数论的知识)
一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一一
二. 带符号整数的表示和运算
带符号整数的表示: 原码、反码、补码
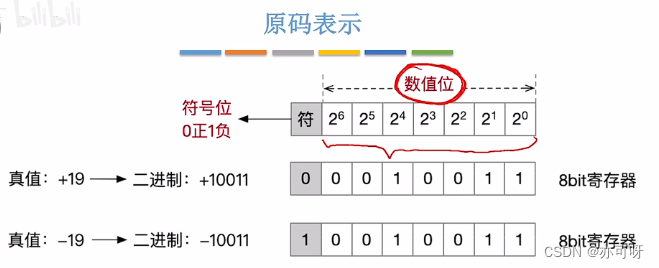
最左边那位为符号位, 符号位为0表示整数, 符号位为1表示负数

quad
2.1 原码、反码、补码的转换
quad
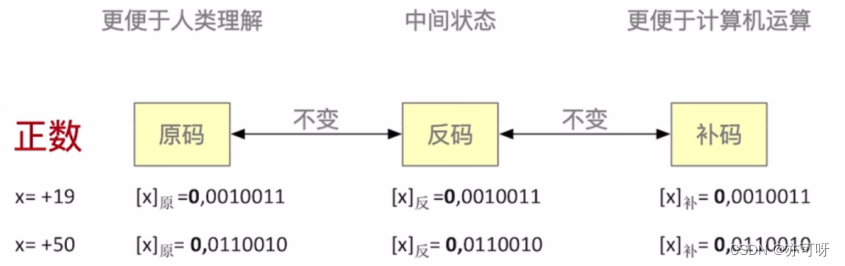
正数的原码、反码、补码都是一样的
补码更便于计算机运算, 所以计算机都是以补码的形式存储数据
(计算机只存储二进制数据的原因,因为计算机由逻辑电路组成,而逻辑电路通常只有两种状态,即高电平和低电平,刚好可以表示成‘1’和‘0’。计算机为了设计简单,只设计了加数寄存器,通过补码的形式可以将减法转换为加法)
quad
quad
quad
quad

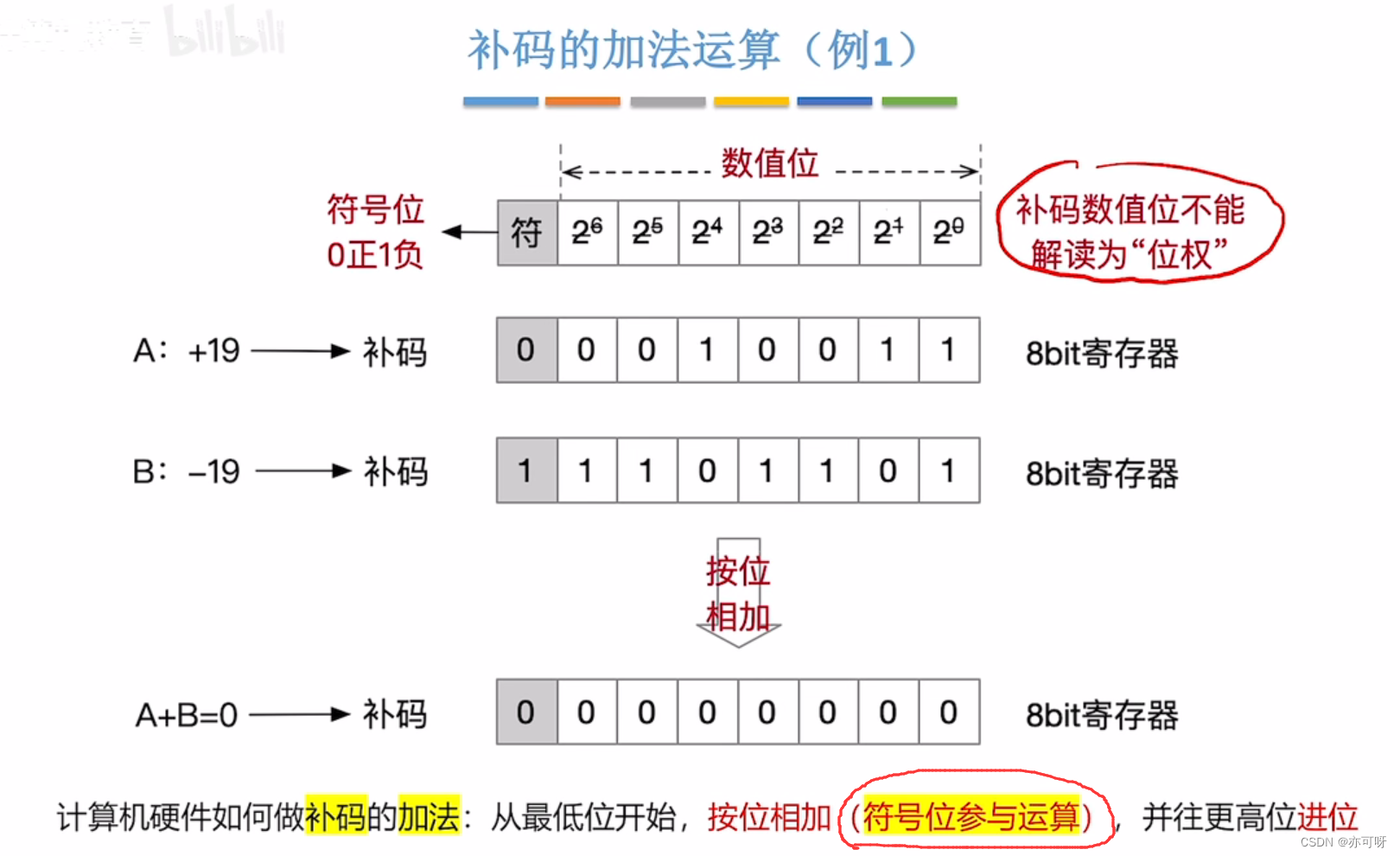
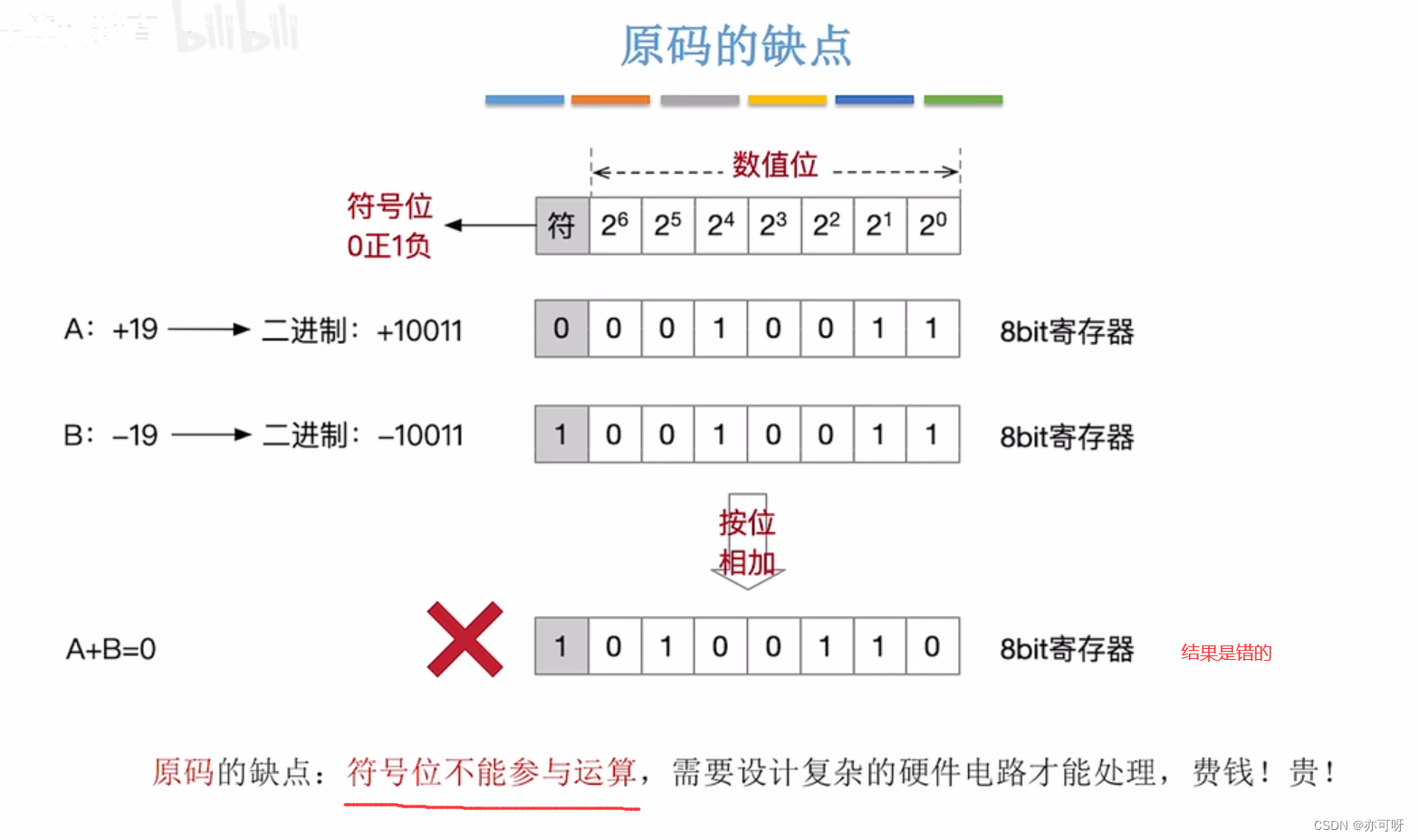
正数还行, 负数的补码数值位不能解读为”位权”, 要先转化为原码才行
quad
2.2 补码的减法运算
quad
还是那个问题: Tips: 加法电路造价便宜,减法电路造价昂贵, 若可将减法转变为加法,省钱!

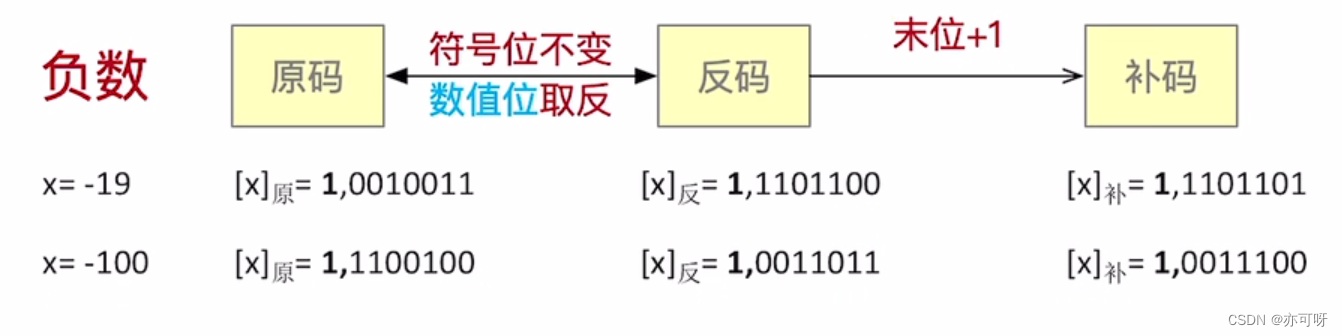
那么如何求负数的补码表示

注意是全部位,当然也包括符号位

注意和无符号数减法比较
quad
三. 原反补码的特性对比
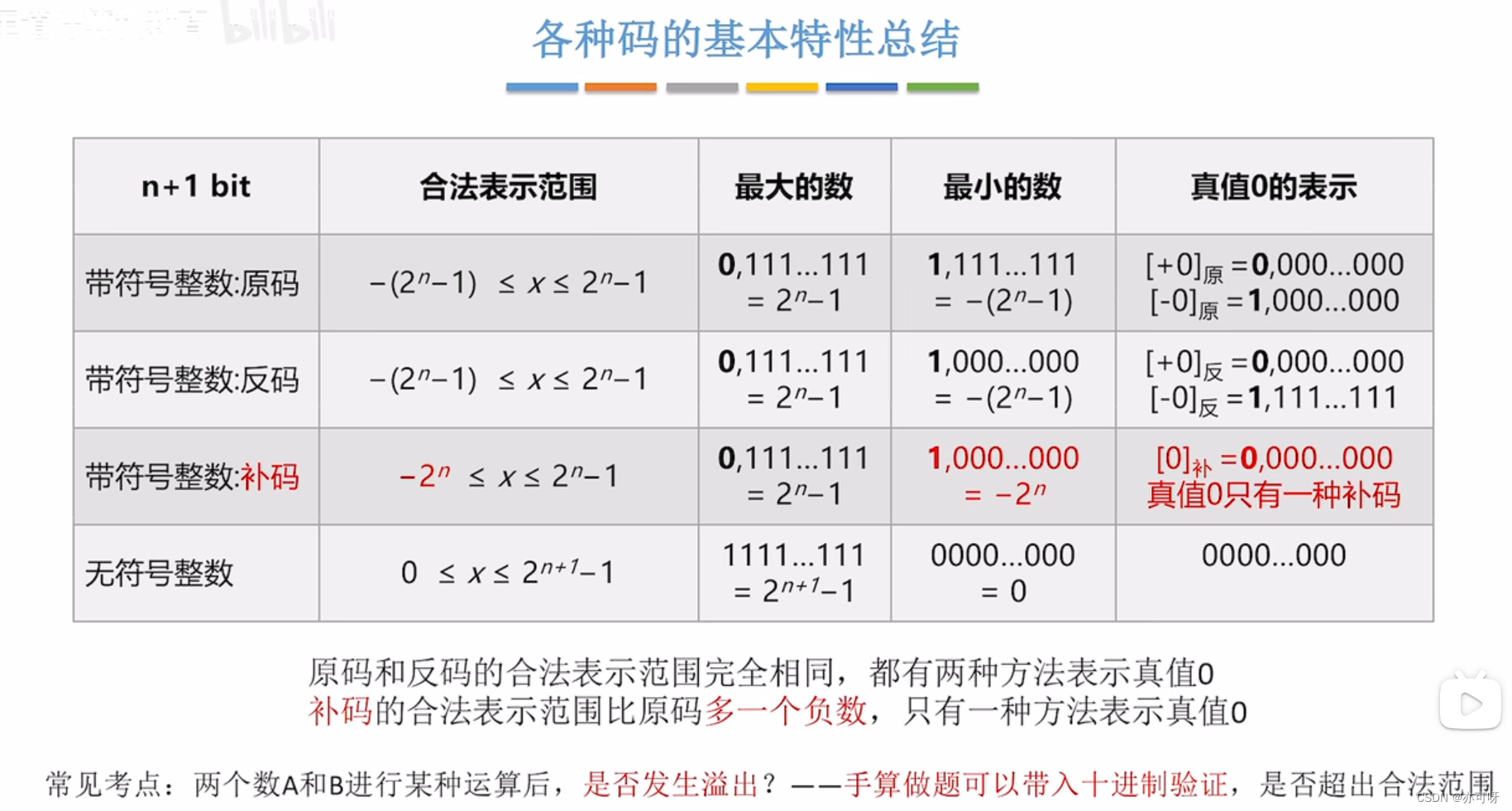
注意补码的合法表示范围
原文地址:https://blog.csdn.net/qq_61866637/article/details/134720572
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。
如若转载,请注明出处:http://www.7code.cn/show_25162.html
如若内容造成侵权/违法违规/事实不符,请联系代码007邮箱:suwngjj01@126.com进行投诉反馈,一经查实,立即删除!





