leetcode – 295. Find Median from Data Stream

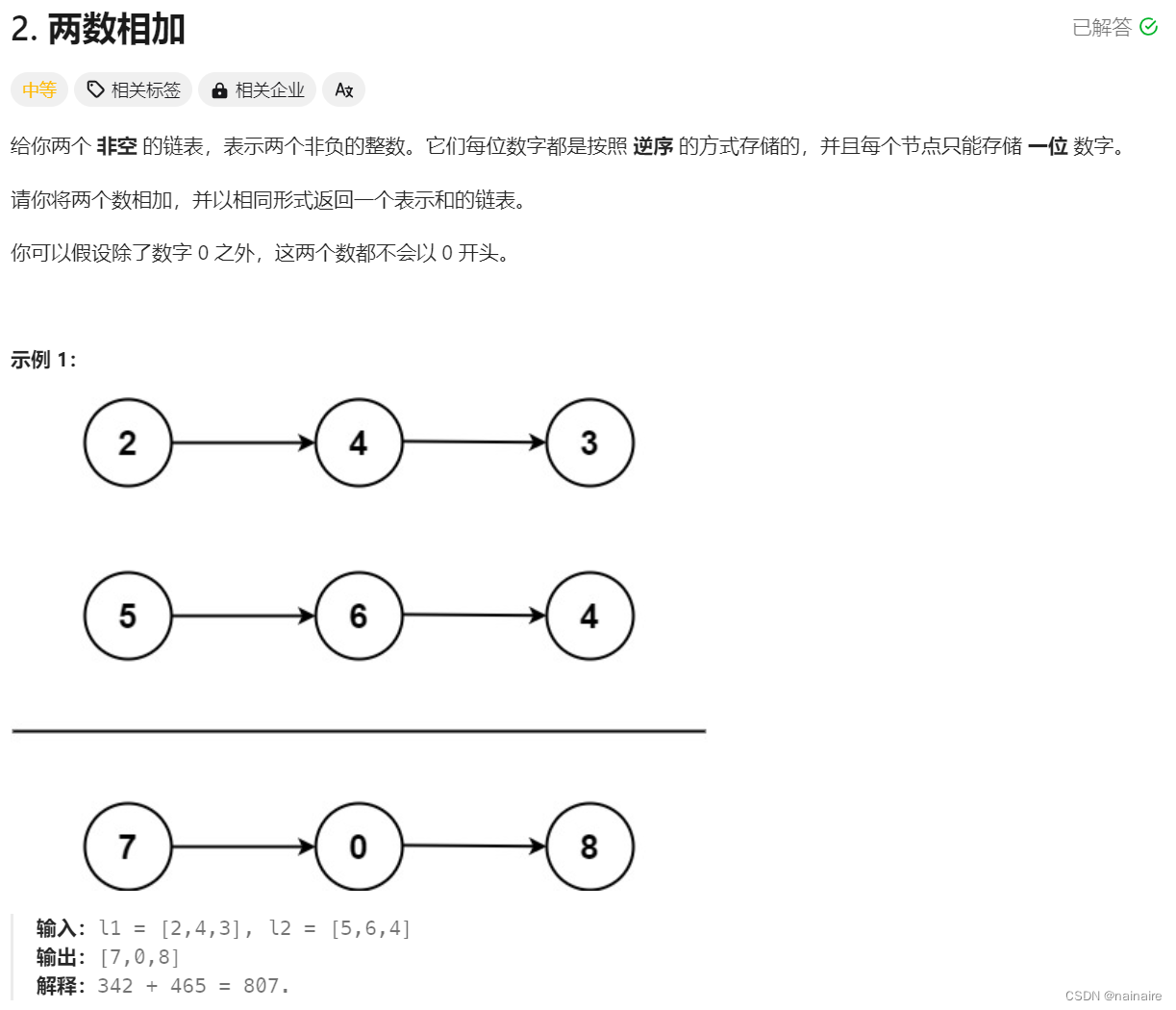
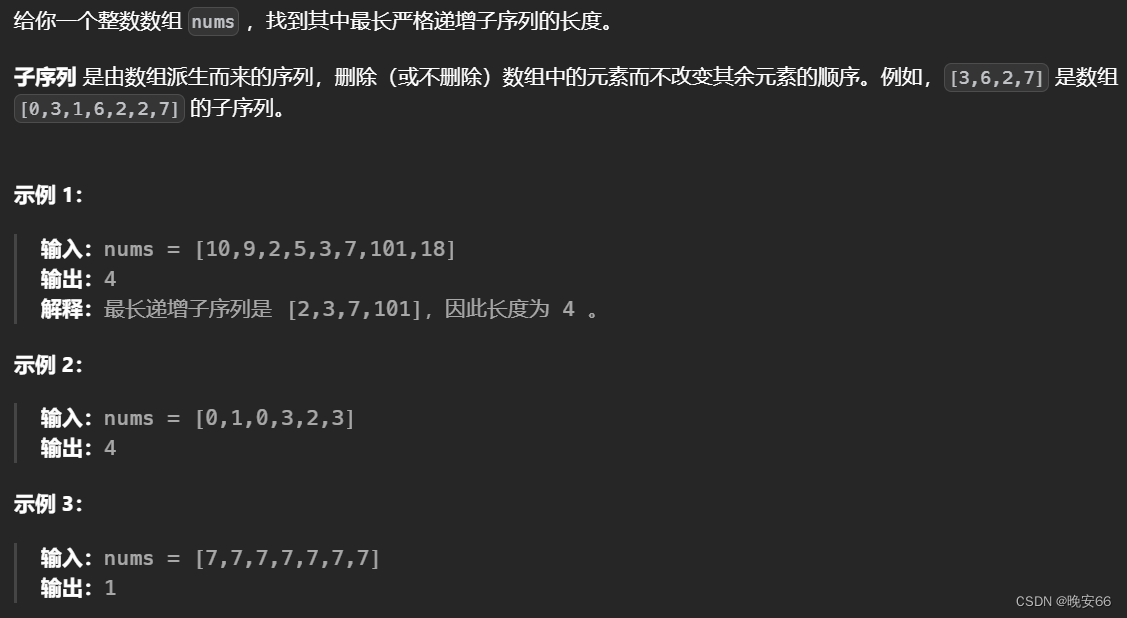
De script ion

The median i s the middle value in an ordered integer list. If the size of the list i s even, there is no middle value, and t he median is t he mean of the two middle values.

For example, for arr = [2,3,4], the median is 3.
For example, for arr = [2,3], the median is (2 + 3) / 2 = 2.5.
Implement the MedianFinder class:

Medi anFin der() initializes the Medi anFin der object.
void addNum(int num) add s the integer num fro m the data stream to the data structure.
double findMedi an() return s the median of all elements so far. Answers within 10-5 of the actual answer will be accepted.

Ex ample 1:

Input
["MedianFinder", "addNum", "addNum", "findMedian", "addNum", "findMedian"]
[[], [1], [2], [], [3], []]
Output
[null, null, null, 1.5, null, 2.0]

Explanation
MedianFinder medianFinder = new MedianFinder();
medianFinder.addNum(1);    // arr = [1]
medianFinder.addNum(2);    // arr = [1, 2]
medianFinder.findMedian(); // return 1.5 (i.e., (1 + 2) / 2)
medianFinder.addNum(3);    // arr[1, 2, 3]
medianFinder.findMedian(); // return 2.0

Constrain ts:

-10^5 <= num <= 10^5
There will be at least one element in the data structure before calling findMedian.
At most 5 * 104 calls will be made to addNum and findMedian.

Follow up:

If all integer numbers from the stream are in the range [0, 100], how would you optimize your solution?
If 99% of all integer numbers from the stream are in the range [0, 100], how would you optimize your solution?

Solution

Solved after help.

Use 2 heaps to store all the numbers, large heap store all the lar ge half of numbers, and small stores all the small half of numbers. large is a min–root heap, and small is a big-root heap. When we need to ca lc ulate the median, just find the top element of each heap.

To maintain their property, every time there’s a new number, push it into one heap, and then p op from the heap to another. For example, let’s sa y we res train the size of small to be n//2, then when their sizes are the same, the next new element go es to large.

When adding the element, firstly add the element into small, and p op one el ement from small to add into large, by doing so we could make sure all the elements in large are larger than small.
Similarly, when adding an el ement into small, firstly add the element into large, then p op one element from large and add it to small.

Time com plexity:

(

log

⁡

)

o(n log n)

$o (n lo g n)$ for adding,

(

)

o(1)

$o (1)$ for get median.
Space complexity:

(

)

o(n)

$o (n)$

Code

class MedianFinder:

    def __init__(self):
        self.small = []
        self.large = []


    def addNum(self, num: int) -> None:
        if len(self.small) == len(self.large):
            heapq.heappush(self.large, -heapq.heappushpop(self.small, -num))
        else:
            heapq.heappush(self.small, -heapq.heappushpop(self.large, num))
        

    def findMedian(self) -> float:
        if len(self.small) == len(self.large):
            return (self.large[0] - self.small[0]) / 2
        else:
            return self.large[0]
        


# Your MedianFinder object will be instantiated and called as such:
# obj = MedianFinder()
# obj.addNum(num)
# param_2 = obj.findMedian()