视觉测量基础

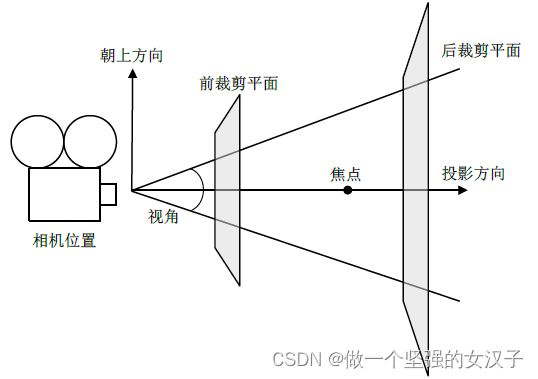
1. 相机模型

1.1 坐标系转换原理

世界坐标系(world Coords):点在真实世界中的位置，描述相机位置。

相机坐标系(Cameras Coords):以相机光学系统中心（镜头中心）为原点，建立相机坐标系。
图像物理坐标系(Film Coords):经过小孔成像后得到的二维坐标系，单位mm。

像素坐标系(Pixel Coords):成像点在相机 sensor上像素的行数和列数，原点为图像左上角，不带有任何物理单位，或者说单位是pixel。
主点:主光线与像平面相交的位置，这个交点取决于镜头的光轴，一般情况下图像中心不可能和主点严格对准。

像素坐标系uv-图像坐标系xy-相机坐标系c-世界坐标系w

其中从像素坐标系-相机坐标系的转换为：

 如果世界坐标系是相对相机坐标系在方向平移了距离d，且，则旋转矩阵R=I，平移矩阵T=，则

 1.2 镜头畸变

径向畸变

切向畸变

2. 相机标定

2.1 相机内参（矩阵）

matlab标定：拍摄的多张图片中最终会计算出唯一的内参M，而外参每张图片都会对应有一个，由于我们的目的是为了测量目标点到相机位置的横纵向距离，所以可以将Zw值设置为0；世界坐标系的原点默认为棋盘格左上角的交点。

2.2 相机外参

取实际工作平面标定得到的外参矩阵R、T。 

2.3 张正友标定法

在多个视点采集平面标定板的图像，使用五参数摄像机模型和四阶透镜变形的径向畸变模型。

在不考虑畸变的情况下，初次标定内参的五个参数，接着使用内参对畸变系数进行标定，重复循环计算直到收敛。使用极大似然法计算单应性矩阵，代入标定图像数据，计算相机内参。继续计算外参和畸变系数。

参考：https://zhuanlan.zhihu.com/p/445872994?utm_medium=social&utm_oi=746817410819977216

3. 距离测量 

坐标系转换

使，将内参矩阵和外参矩阵参数代入，可求得，实际上在坐标系的转换中可以被消掉，不影响计算过程。

参考：单目相机测距

代码007普通

打赏 收藏 海报 链接