堆
堆是将一组数据按照完全二叉树的存储顺序,将数据存储在一个一维数组中的结构。
大顶堆
大顶堆的任何一个父节点的值,都大于或等于它左、右孩子 节点的值。

小顶堆
最小堆的任何一个父节点的值,都小于或等于它左、右孩子 节点的值。

堆的根节点叫作堆顶
大顶堆和小顶堆的特点决定了:大顶堆的堆顶是整个堆中的最大元素;小顶堆的堆顶是整个堆中的最小元素。
堆的自我调整
所谓堆的自我调整,就是把一个不符合堆性质的完全二叉树,调整成一个堆 .
插入节点
当堆插入节点时,插入位置是完全二叉树的最后一个位置。例如插入一个 新节点,值是 0

这时,新节点的父节点 5 比 0 大,显然不符合最小堆的性质。于是让新节点“上 浮”,和父节点交换位置
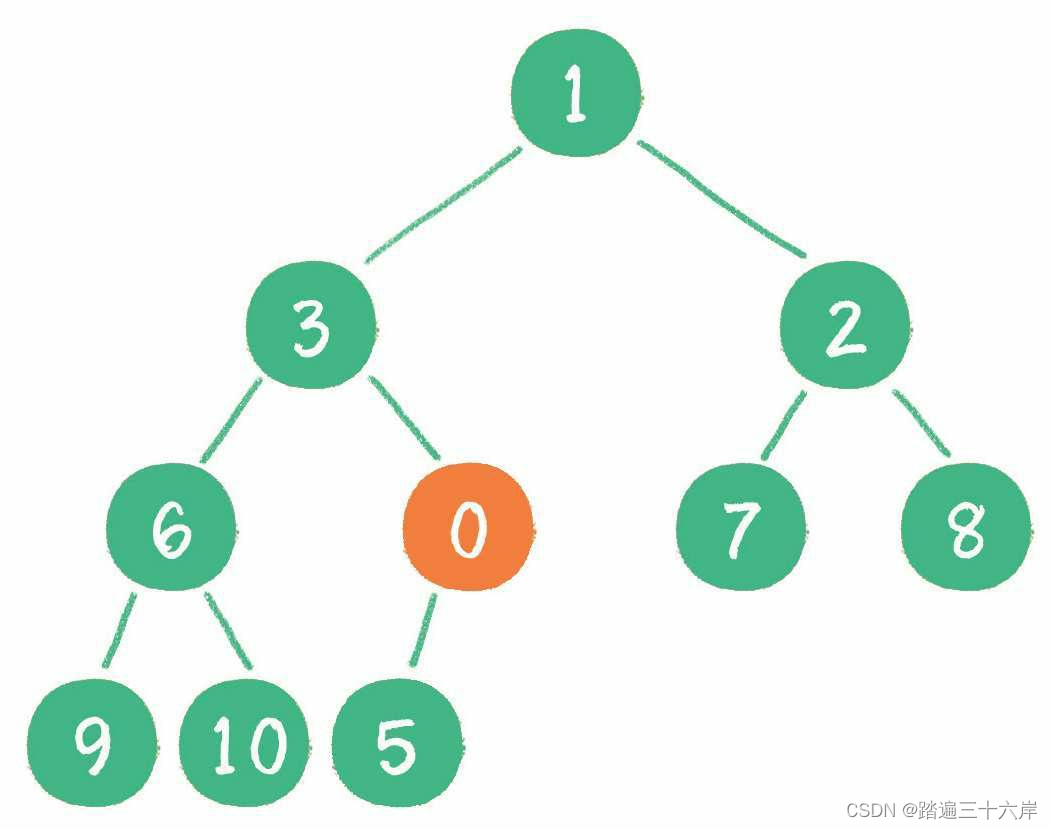
继续用节点 0 和父节点 3 做比较,因为 0 小于 3,则让新节点继续“上浮”
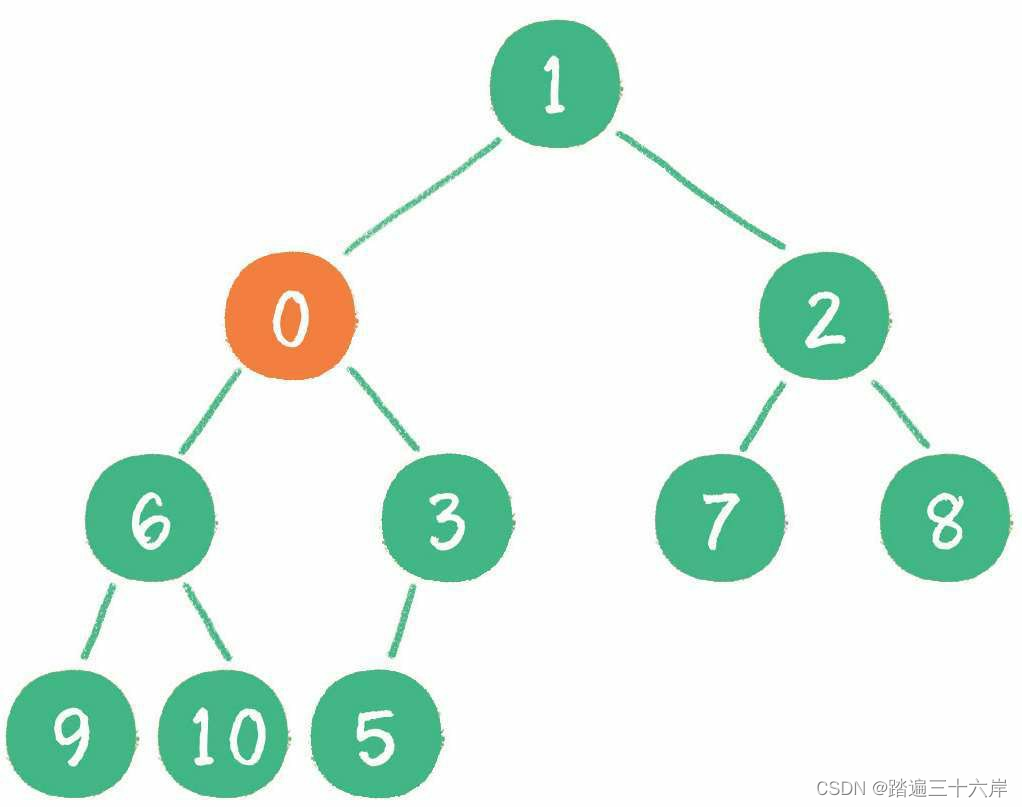

这就是插入的过程 .
删除节点
堆删除节点的过程和插入节点的过程正好相反,所删除的是处于堆顶的节点。例如删除最小堆的堆顶节点 1
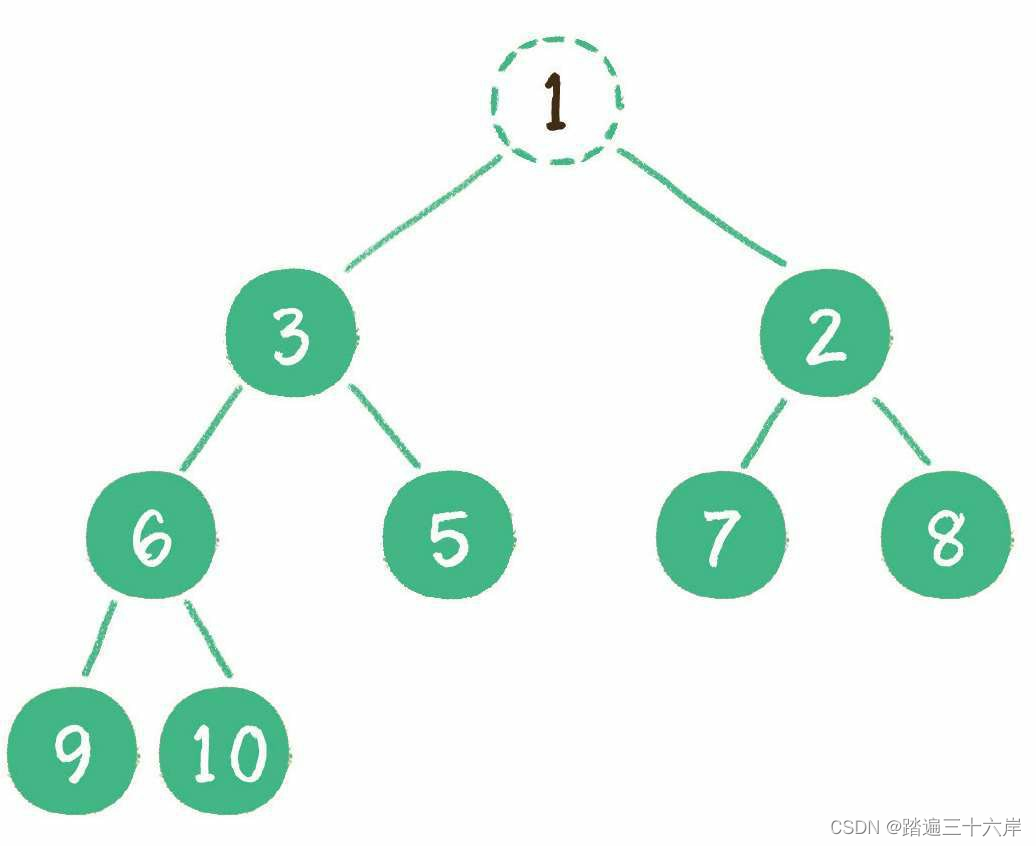
这时,为了继续维持完全二叉树的结构,我们把堆的最后一个节点 10 临时补到 原本堆顶的位置

接下来,让暂处堆顶位置的节点10和它的左、右孩子进行比较,如果左、右孩子节点中最小的一个(显然是节点2)比节点10小,那么让节点10“下沉”
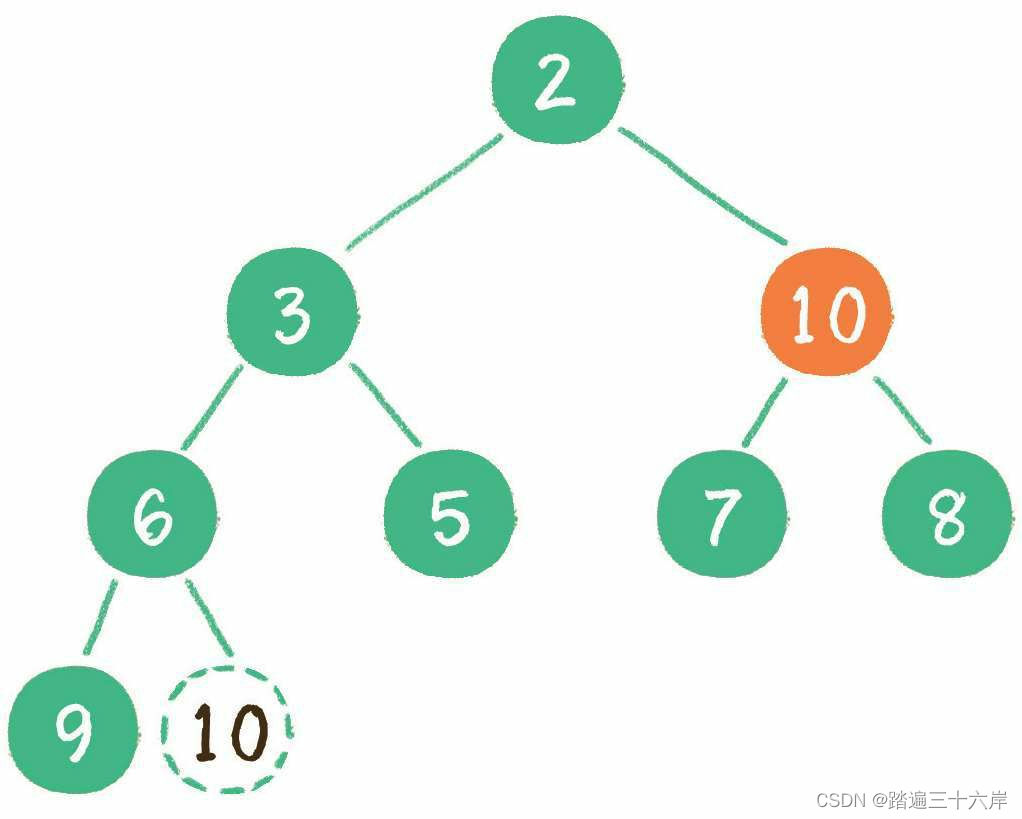
继续让节点10和它的左、右孩子做比较,左、右孩子中最小的是节点7,由于10 大于7,让节点10继续“下沉”
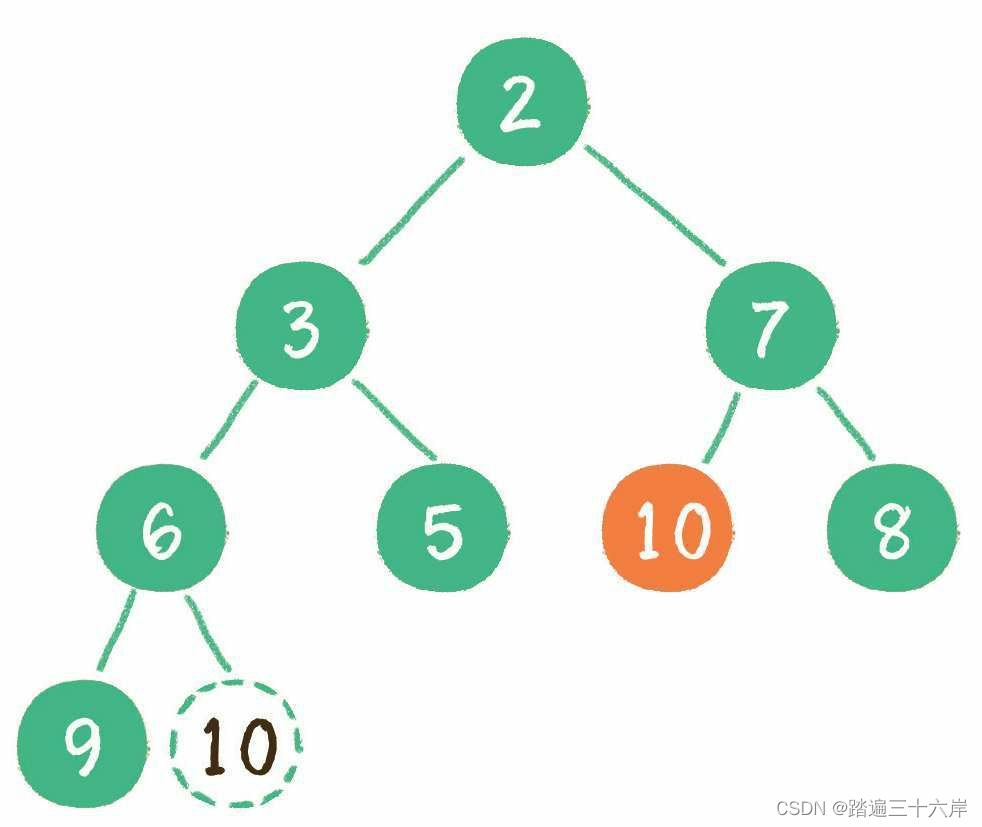
这样一来,二叉堆重新得到了调整
大家好好理解一下 .
这期就到这里 , 下期见!
原文地址:https://blog.csdn.net/sytdsqzr/article/details/134741539
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。
如若转载,请注明出处:http://www.7code.cn/show_27024.html
如若内容造成侵权/违法违规/事实不符,请联系代码007邮箱:suwngjj01@126.com进行投诉反馈,一经查实,立即删除!