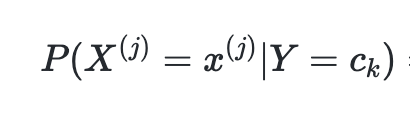机器学习实战：Python基于朴素贝叶斯Bayes进行分类预测（二）

本文介绍: 朴素贝叶斯（）是一种基于贝叶斯定理的分类算法，它假设各个特征之间相互独立，因此可以通过计算每个特征的条件概率来预测类别。该算法通常用于文本分类和垃圾邮件过滤等任务。朴素贝叶斯模型易于实现，计算速度快。即使特征之间存在一定的相关性，朴素贝叶斯模型仍然可以处理。适用于高维数据集，并且在小数据集上也能表现良好。朴素贝叶斯模型假设特征之间相互独立，这在实际情况下很少成立。朴素贝叶斯模型对输入数据的准确性要求较高，如果输入数据有误差，则会导致错误的预测。朴素贝叶斯模型通常需要更多的数据才能获得更好的分类效果。

文章 目录

1 前言

1.1 朴素 贝叶斯的介绍

朴素贝叶斯（Nai v e Ba y es）是一种基于贝叶斯定理的分类算法，它假设各个特征之间相互独立，因此可以通过计算每个特征的条件概率来预测类别。该算法通常用于文本分类和垃圾邮件过滤等任务。

优点：

朴素贝叶斯模型易于实现，计算速度快。
即使特征之间存在一定的相关性，朴素贝叶斯模型仍然可以处理。
适用于高维数据集，并且在小数据集上也能表现良好。

缺点：

朴素贝叶斯模型假设特征之间相互独立，这在实际情况下很少成立。
朴素贝叶斯模型对输入数据的准确性要求较高，如果输入数据有误差，则会导致错误的预测。
朴素贝叶斯模型通常需要更多的数据才能获得更好的分类效果。

1.2 朴素贝叶斯的应用

朴素贝叶斯是一种常见的分类算法，主要应用于以下领域：

文本分类：朴素贝叶斯是文本分类任务中常用的算法，例如垃圾邮件分类、情感分析等。
推荐系统：朴素贝叶斯可以用于对用户进行分类，例如将用户分为购买和不购买两类，进而进行个性化推荐。
生物信息学：朴素贝叶斯可以用于分析基因表达数据和基因序列。
金融风险评估：朴素贝叶斯可以用于评估贷款申请者的信用风险。
医学诊断：朴素贝叶斯可以用于预测患病概率，例如预测某种疾病的患病率或判断某种疾病的诊断结果等。

2 iris数据集演示

2.1 导入 函数

import warnings
warnings.filterwarnings('ignore')
import numpy as np

# 加载数据集
from sklearn import datasets

# 导入高斯朴素贝叶斯分类器
from sklearn.naive_bayes import GaussianNB
from sklearn.model_selection import train_test_split

2.2 导入数据

# 例行公事，训练集测试集还是7/3分
X, y = datasets.load_iris(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)

2.3 训练模型

# 使用高斯朴素贝叶斯进行计算
clf = GaussianNB(var_smoothing=1e-8)
clf.fit(X_train, y_train)

2.4 预测模型

# 评估
y_pred = clf.predict(X_test)
acc = np.sum(y_test == y_pred) / X_test.shape[0]
print("Test Acc : %.3f" % acc)

# 预测
y_proba = clf.predict_proba(X_test[:1])
print(clf.predict(X_test[:1]))
print("预计的概率值:", y_proba)

高斯朴素贝叶斯假设每个特征都服从高斯分布，我们把一个随机变量X服从数学期望为μ，方差为σ^{2的数据分布称为高斯分布。对于每个特征我们一般使用平均值来估计μ和使用所有特征的方差估计σ}2

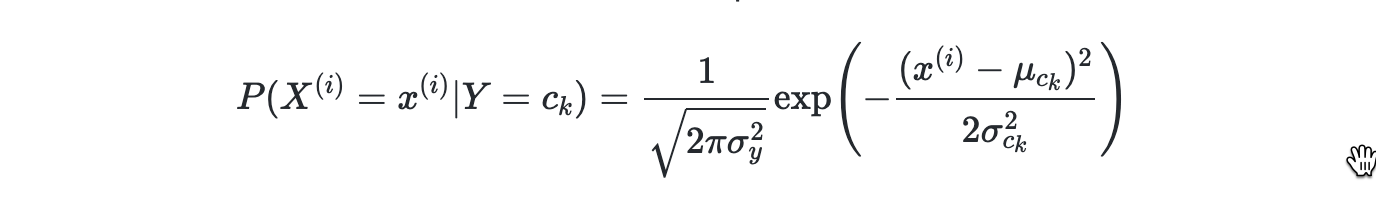
Acc能达到1，一如既往的nice；根据结果计算后类别2对应的后验概率值最大，所以我们认为类别2是最优的结果

3 模拟 离散数据演示

3.1 导入函数

import random
import numpy as np
# 使用基于类目特征的朴素贝叶斯
from sklearn.naive_bayes import CategoricalNB
from sklearn.model_selection import train_test_split

3.2 模拟/导入数据

# 模拟数据
rng = np.random.RandomState(1)
# 随机生成600个100维的数据，每一维的特征都是[0, 4]之前的整数
X = rng.randint(5, size=(600, 100))
y = np.array([1, 2, 3, 4, 5, 6] * 100)
data = np.c_[X, y]
# X和y进行整体打散
random.shuffle(data)
X = data[:,:-1]
y = data[:, -1]
# 还是继续7/3分
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)

3.3 训练模型

clf = CategoricalNB(alpha=1)
clf.fit(X_train, y_train)
acc = clf.score(X_test, y_test)
# 评估
print("Test Acc : %.3f" % acc)

Acc大大降低了，只有个0.65，没办法，毕竟是个随机数据集，所以不具备太多但是为了满足自己的小小心思，写了个for循环，简单设置随机种子取1至1000，大于一个值跳出循环，反复试了几次，最高仅能过0.7，0.75都达不到。服务器试的，1000个循环个人PC还是尽量不要试了。

3.4 预测模型

x = rng.randint(5, size=(1, 100))
print(clf.predict_proba(x))
print(clf.predict(x))

预测结果是4

4 原理补充说明

4.1 贝叶斯算法

关于alpha=1这个参数的含义，首先要明确贝叶斯法需要计算的两个概率：

条件概率
类目 ck 的先验概率

对每一个变量的多加了一个频数alpha。当alphaλ=0时，就是极大似然估计。通常取值alpha=1，这就是拉普拉斯平滑(Laplace smoothing)，这有叫做贝叶斯估计，主要是因为如果使用极大似然估计，如果某个特征值在训练数据中没有出现，这时候会出现概率为0的情况，导致整个估计都为0，因为引入贝叶斯估计。