前言
今天我想把前面未更新完的排序算法补充一下,也就是基数排序的一种,这是跟计数排序一样类型的排序算法,是属于非比较型的排序算法,下面我们就一起来看看吧。
基数排序
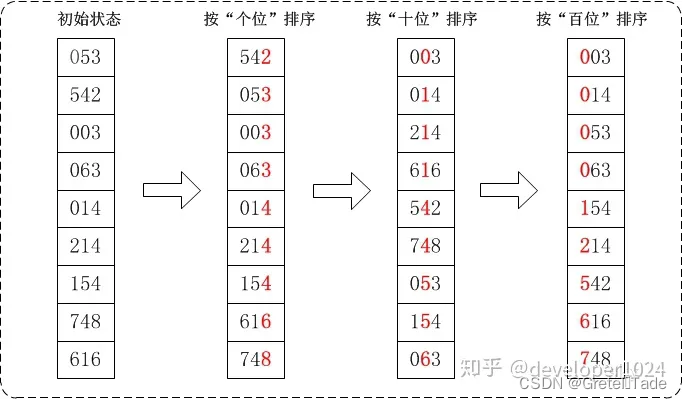
基数排序的发明可以追溯到1887年赫尔曼·何乐礼在打孔卡片制表机 (Tabulation Machine)上的贡献。它是这样实现的:将所有待比较数值(正整数)统一为同样的数位长度,数位较短的数前面补零。然后,从最低位开始,依次进行一次排序。这样从最低位排序一直到最高位排序完成以后, 数列就变成一个有序序列。 基数排序的方式可以采用LSD(Least significant digital)或MSD(Most significant digital),LSD的排序方式由键值的最右边开始,而MSD则相反,由键值的最左边开始。
算法思想
 上面这些理论思想看上去不太好理解,那下面我举个例子去简单解释一下。
上面这些理论思想看上去不太好理解,那下面我举个例子去简单解释一下。
算法示例
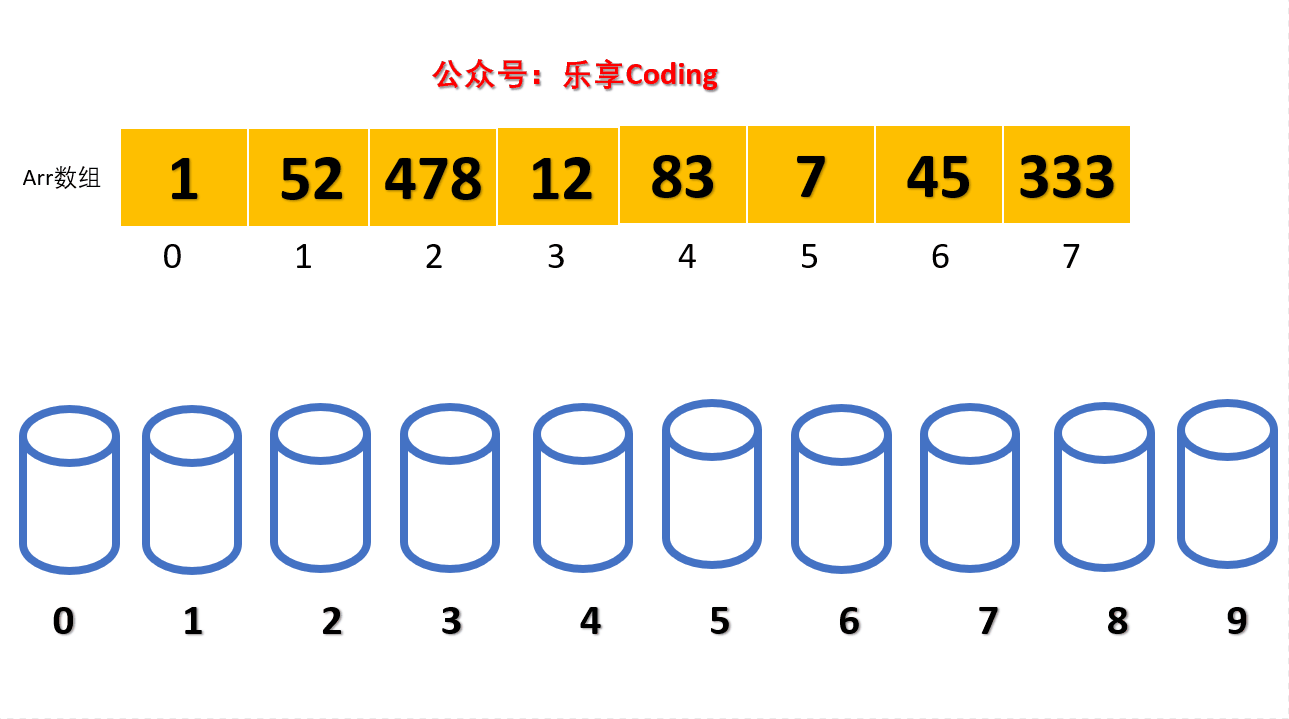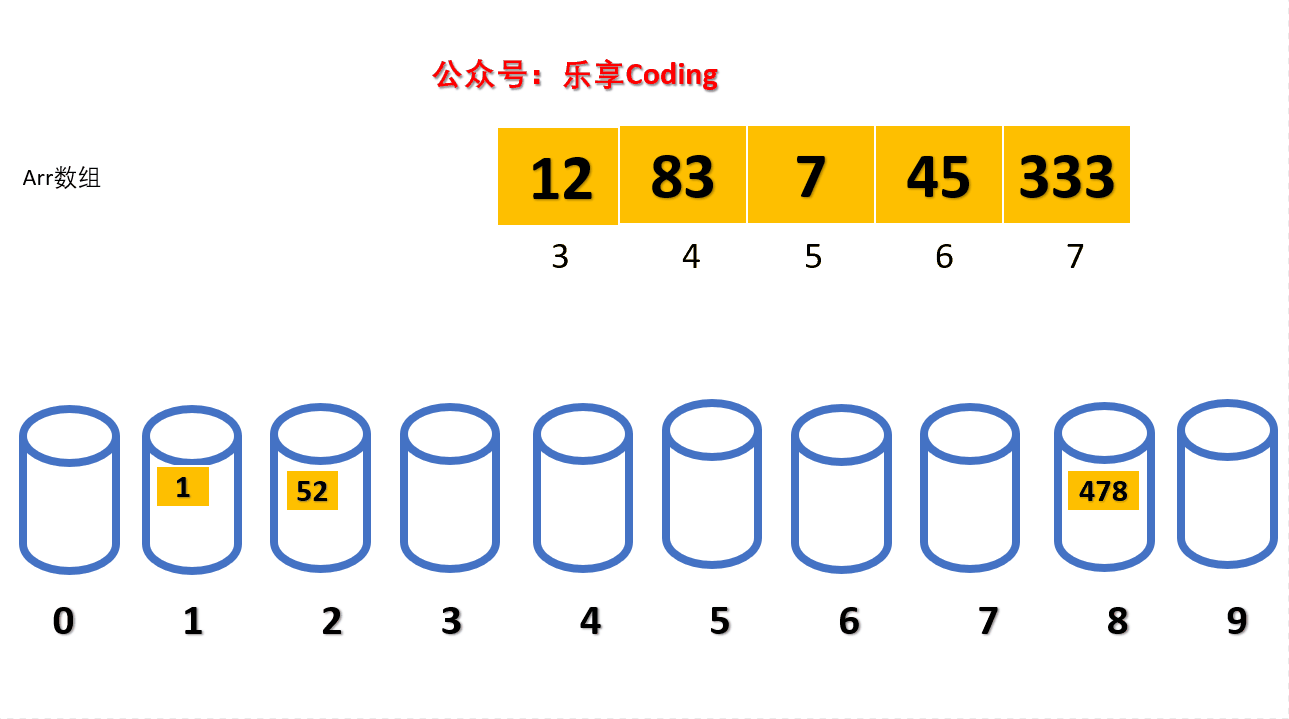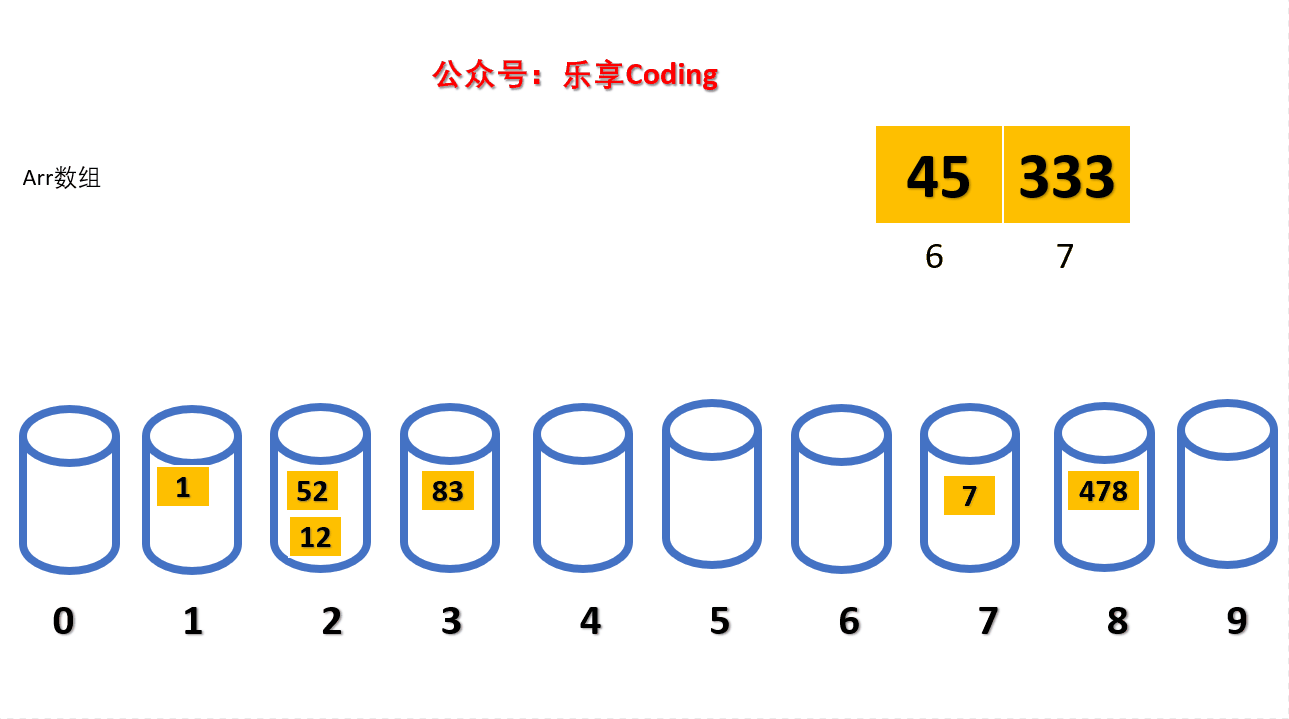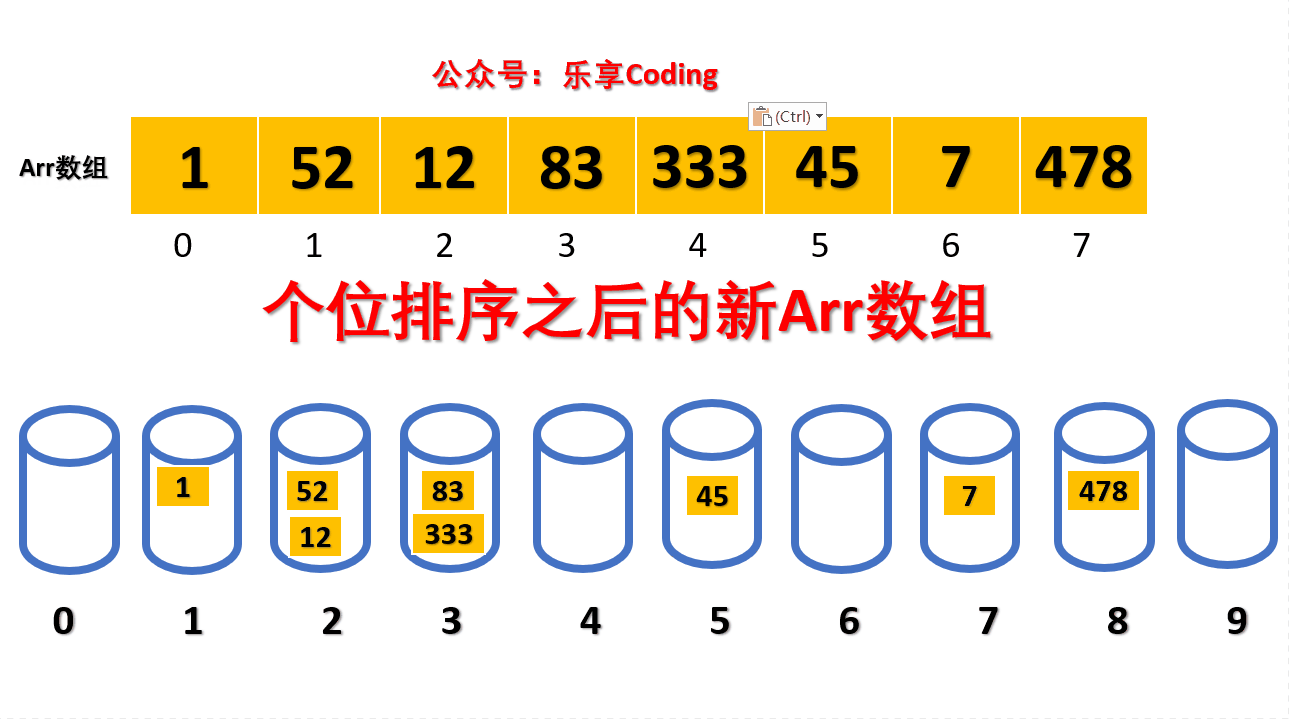
比如有这么一个数组 array = {53, 3, 542, 748, 14, 214, 154, 63, 616} 现在要去进行基数排序。
这里我们需要去创建一个长度为10的队列数组。Queue que[10]。然后这个队列数组作为根据基数储存数据的队列表。
这里,我们对数组中的每一个数字去进行遍历,然后进行按位求余,最先是个位数,得到的结果,根据对应的队列数组下标去进行入队操作。基数分配结果如下所示:
que[3]—–>53——>3—–>63—–>NULL
que[4]—–>14—–>214—–>154—–>NULL
que[5]—–>NULL
que[6]—–>616—–>NULL
que[7]—–>NULL
que[8]—–>748—–>NULL
que[9]—–>NULL
然后根据第一次基数计算出的结果,重新去排放这个数组,对这个队列表进行遍历(从上到下),然后出队操作,出队的结果放入到数组当中,第一次数组更新结果如下:
[ 542, 53, 3, 63, 14, 214, 154, 616, 748 ]
在进行第二次分配的时候,我们就根据上面已经跟新好了的数组去重新分配,这一次我们就要去进一位来分配。结果如下:
que[0]—–>3—–>NULL
que[1]—–>14—–>214—–>616—–>NULL
que[2]—–>NULL
que[3]—–>NULL
que[4]—–>542—–>748—–>NULL
que[5]—–>53—–>154—–>NULL
que[6]—–>63—–>NULL
que[7]—–>NULL
que[8]—–>NULL
que[9]—–>NULL
根据第二次基数计算出的结果,重新去排放这个数组,对这个队列表进行遍历(从上到下),然后出队操作,出队的结果放入到数组当中,第二次数组更新结果如下:
[ 3, 14, 214 ,616, 542, 748, 53, 154, 63 ]
我们接着取上面第二次分配的数组结果,然后再次根据百位数求余数分配。结果如下:
que[0]—–>3—–>14—–>53—–>63—–>NULL
que[1]—–>154—–>NULL
que[2]—–>214—–>NULL
que[3]—–>NULL
que[4]—–>NULL
que[5]—–>542—–>NULL
que[6]—–>616—–>NULL
que[7]—–>748—–>NULL
que[8]—–>NULL
que[9]—–>NULL
根据第三次基数计算出的结果,重新去排放这个数组,对这个队列表进行遍历(从上到下),然后出队操作,出队的结果放入到数组当中,第三次数组更新结果如下:
[ 3, 14, 53, 63, 154, 214, 542, 616, 748 ]
这里我们可以看出,已经拍好序了,但是我建议还是继续去第四次分配,直到全部的数字都在队列que[0]上。
第四次基数分配(根据千位数分配)
同样的,这里我们把基数再进一位
que[0]—–>3—–>14—–>53—–>63—–>154—–>214—–>542—–>616—–>748—–>NULL
que[1]—–>NULL
que[2]—–>NULL
que[3]—–>NULL
que[4]—–>NULL
que[5]—–>NULL
que[6]—–>NULL
que[7]—–>NULL
que[8]—–>NULL
que[9]—–>NULL
此时的全部数字都在第一个队列上,这时候就完成了排序,只需要去对这个队列进行出队,然后把数据重新放入到数组当中,结果如下,至此,排序结束。
[ 3, 14, 53, 63, 154, 214, 542, 616, 748 ]
动态图:
代码实现
1.队列queue.h 头文件
#pragma once
#include<stdlib.h>
//数据类型
typedef int Datatype;
//节点
typedef struct node {
Datatype data;
struct node* next;
}Lnode;
//队列
typedef struct queue {
int curnum;
Lnode* front, * rear;
}Queue;
//队列初始化
void queue_init(Queue* que);
//判空
int isEmpty(Queue q);
//入队列
void enqueue(Queue *que, Datatype data);
//出队列
Lnode* dequeue(Queue* que);
//获取队头元素
Datatype get_headdata(Queue que);2.队列queue.c 源文件
#include"queue.h"
#include<assert.h>
//队列初始化
void queue_init(Queue* que) {
que->curnum = 0;
que->front = que->rear = NULL;
}
//创建一个节点
Lnode* create_node(Datatype data) {
Lnode* node = (Lnode*)malloc(sizeof(Lnode));
assert(node);
node->data = data;
node->next = NULL;
return node;
}
//判空
int isEmpty(Queue q) {
return q.curnum == 0;
}
//入队列
void enqueue(Queue *que,Datatype data) {
Lnode* add = create_node(data);
if (isEmpty(*que)) {
que->front = que->rear = add;
que->curnum++;
}
else {
que->rear->next = add;
que->rear = add;
que->curnum++;
}
}
//出队列
Lnode* dequeue(Queue *que) {
if (isEmpty(*que))
return NULL;
if (que->curnum == 1)
que->rear = NULL;
Lnode* de = que->front;
que->front = de->next;
que->curnum--;
return de;
}
//获取队头元素
Datatype get_headdata(Queue que) {
return que.front->data;
}3.主函数(radix_sort实现)
#include<stdio.h>
#include<stdlib.h>
#include"queue.h"
void radix_sort(int* arr, int n) {
Queue que[10];//创建下标为0~9的队列
for (int i = 0; i < 10; i++) {
queue_init(&que[i]);//初始化队列
}
for (int i = 0; i < n; i++) {
enqueue(&que[arr[i] % 10], arr[i]);//把数组个位数的数字依次入队
}
int k = 0;
int count = 10;
while (que[0].curnum != n) {//如果数字里面全部的数据到第0个队列的时候就结束
for (int i = 0; i < 10; i++) {
while (!isEmpty(que[i])) {
Lnode* pop = dequeue(&que[i]);//出队
arr[k++] = pop->data;//重新放置数组
//释放空间
free(pop);
pop = NULL;
}
}
k = 0;
for (int i = 0; i < n; i++) {
//除以count取整,此时指向进一位数字,进行入队操作
int x = arr[i] / count;
enqueue(&que[x % 10], arr[i]);
}
count *= 10;//
}
}
int main() {
int array[] = { 123,0, 25,24,6,65,11,43,22,51 ,999 };
printf("排序前:");
for (int i = 0; i < sizeof(array) / sizeof(int); i++) {
printf("%d ", array[i]);
}
//基数排序
radix_sort(array, sizeof(array) / sizeof(int));
printf("n排序后:");
for (int i = 0; i < sizeof(array) / sizeof(int); i++) {
printf("%d ", array[i]);
}
}输出结果:

算法分析
以上就是本期的全部内容了,我们下次见咯~
原文地址:https://blog.csdn.net/m0_73633088/article/details/134613137
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。
如若转载,请注明出处:http://www.7code.cn/show_27762.html
如若内容造成侵权/违法违规/事实不符,请联系代码007邮箱:suwngjj01@126.com进行投诉反馈,一经查实,立即删除!