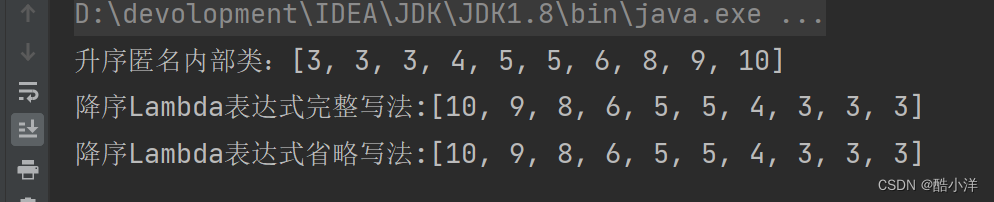
最小多项式
化零多项式:
f
(
A
)
=
O
n
×
n
f(A)=On×n
f
(
λ
)
f(lambda)
f(λ) ,即A 的特征多项式,也是化零多项式。
定义:已知
A
∈
C
n
×
n
A∈Cn×n ,在
A
A
A
A
A 的最小多
项式,通常记为
(
λ
)
(
λ
)
m(λ) 为
(
λ
−
λ
i
)
i
1
(
λ
)
,
2
(
λ
)
,
…
,
(
λ
)
m_1(lambda),m_2(lambda),dots,m_r(lambda)
m1(λ),m2(λ),…,mr(λ)的最小公倍式。

求得最小多项式
m
(
λ
)
=
(
λ
−
λ
1
)
d
1
(
λ
−
λ
2
)
d
2
…
(
λ
−
λ
)
d
large m(lambda) = (lambda-lambda_1)^{d_1}(lambda-lambda_2)^{d_2}dots (lambda-lambda_s)^{d_s}
m(λ)=(λ−λ1)d1(λ−λ2)d2…(λ−λs)ds
写
(
)
=
a
0
+
a
1
+
a
2
2
⋯
+
a
m
−
1
m
−
1
,其中
m
=
∑
i
=
1
s
d
i
f
(
)
=
(
)
f
(
)
(
λ
i
)
=
(
)
(
λ
i
)
,
i
=
1
,
2
,
…
,
s
;
=
1
,
2
,
…
,
d
i
−
1.
解得
a
0
.
a
1
,
…
,
a
m
−
1
后
:
f
(
A
)
=
a
m
−
1
A
m
−
1
+
a
m
−
2
A
m
−
2
+
⋯
+
a
1
A
+
a
0
I
large p(x) = a_0 + a_1x+a_2^2dots+a_{m-1}^{m-1},其中 m = sum_{i=1}^{s}{d_i}\ f(x) = p(x)\ f^{(k)}(lambda_i)=p^{(k)}(lambda_i),i=1,2,dots,s;k=1,2,dots,d_i-1.\ 解得a_0.a_1,dots,a_{m-1}后:\ f(A)=a_{m-1}A^{m-1}+a_{m-2}A^{m-2}+dots+a_1A+a_0I\
p(x)=a0+a1x+a22⋯+am−1m−1,其中m=i=1∑sdif(x)=p(x)f(k)(λi)=p(k)(λi),i=1,2,…,s;k=1,2,…,di−1.解得a0.a1,…,am−1后:f(A)=am−1Am−1+am−2Am−2+⋯+a1A+a0I

求矩阵函数方法一:
求得
J
P
求得J 和 相似变换矩阵 P
求得J和相似变换矩阵P

求矩阵函数方法二:
m
(
λ
)
利用最小多项式m(λ)
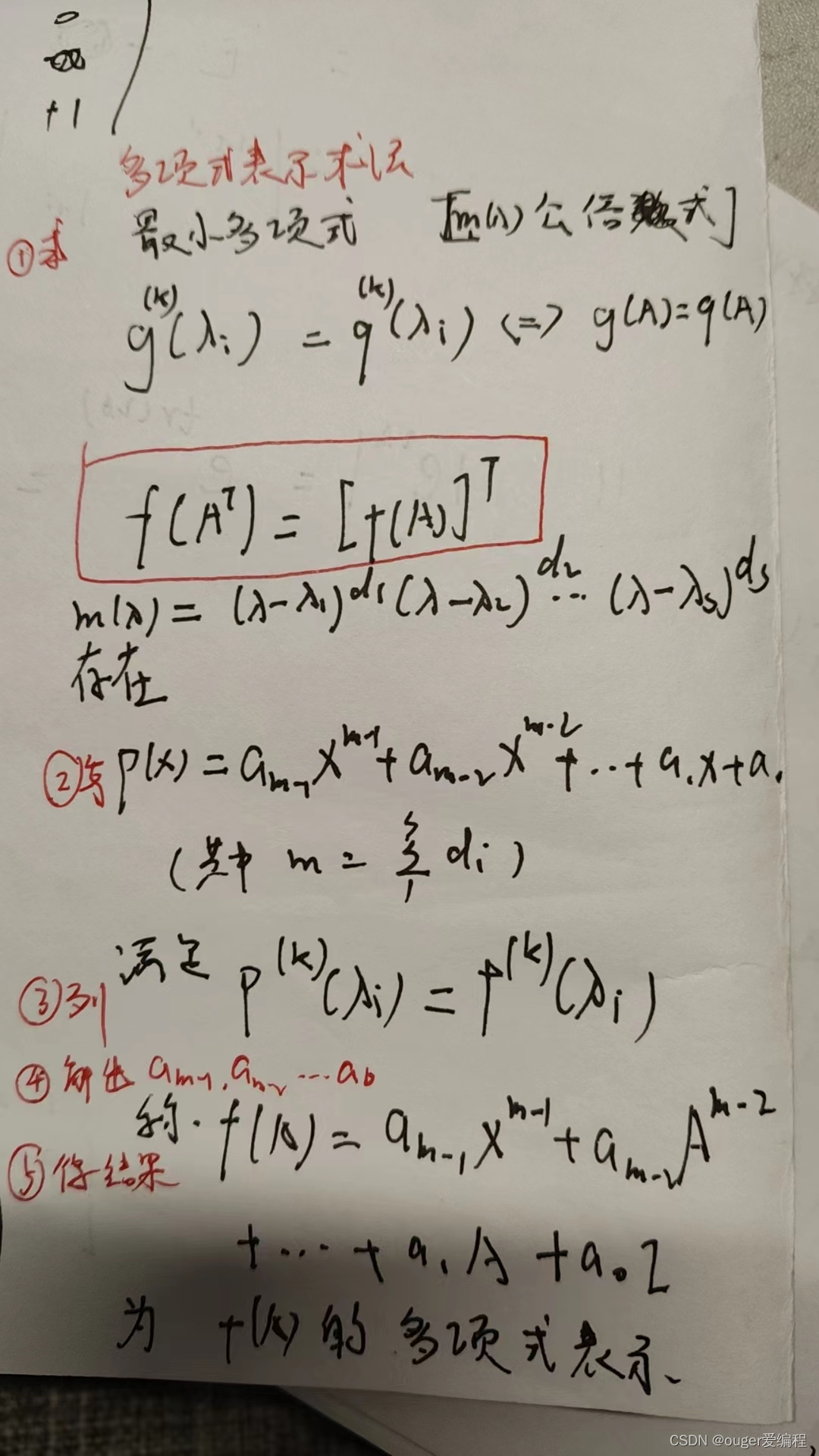
指数矩阵函数和三角矩阵函数:

矩阵函数的幂级数:
原文地址:https://blog.csdn.net/onlyyoujojo/article/details/134618830
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。
如若转载,请注明出处:http://www.7code.cn/show_28280.html
如若内容造成侵权/违法违规/事实不符,请联系代码007邮箱:suwngjj01@126.com进行投诉反馈,一经查实,立即删除!