canvas 凸包效果

前言

微信公众号：前端不只是切图

代码运行的最终效果在文章最后

什么是凸包

本篇文章主要阐述如何在canvas上实现凸包的效果，我们先来看看下什么是凸包，先上附图

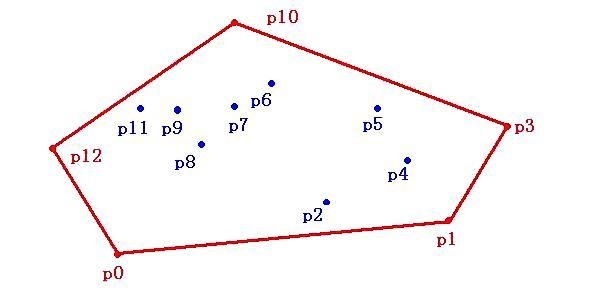
从上面的图可以看出，图中的内容包含点p0-点p12，而红框部分就是凸包，可以看出其由最外围的点连接构成刚好把所有的内容都包住，就像橡皮筋勒紧的效果，当运用到canvas上时，点相当于canvas上的像素

Andrew算法

本文主要使用Andrew算法实现凸包的效果，先上个gif图，看下这个算法的全貌

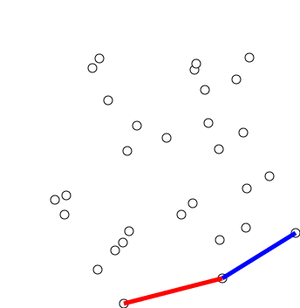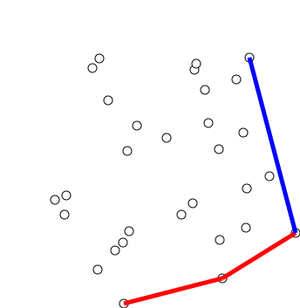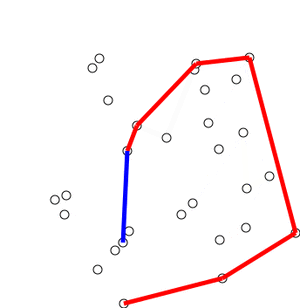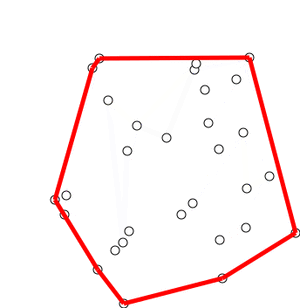
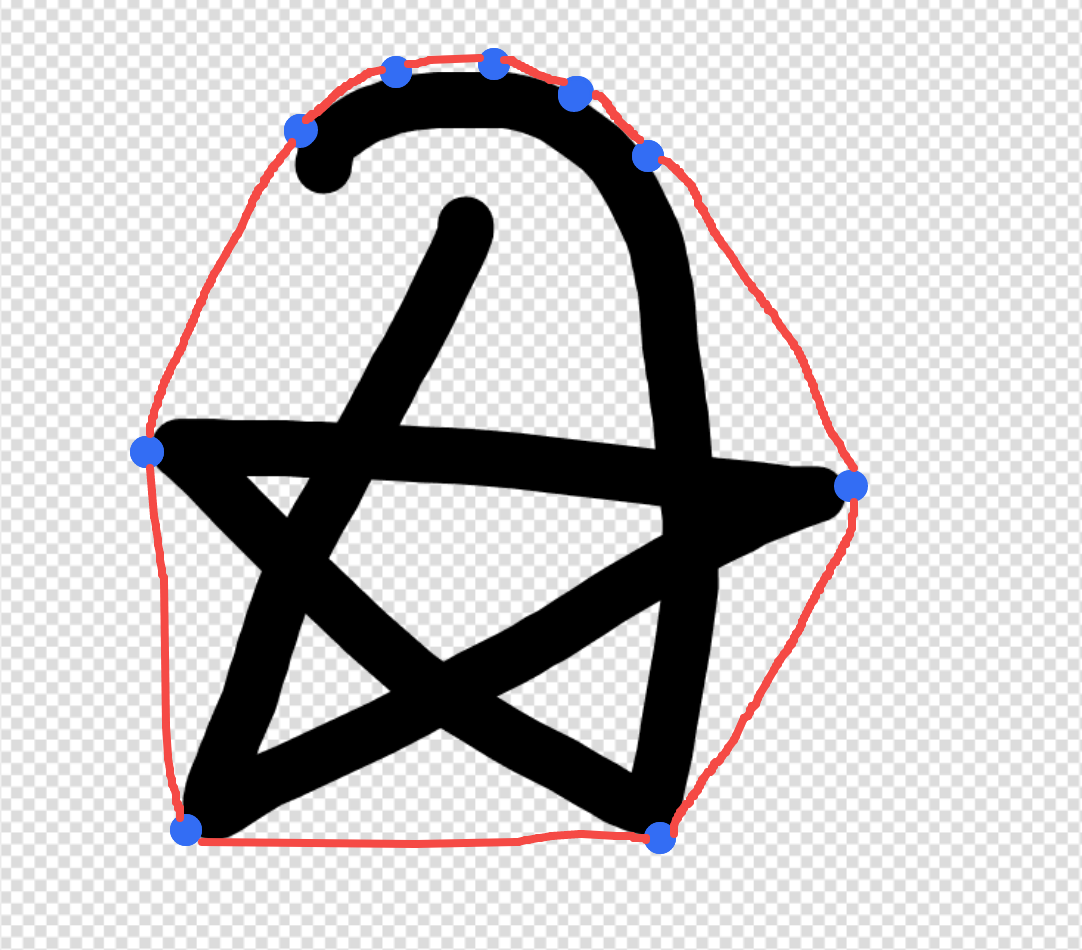
可能刚开始看有点懵逼，没事，其实算法思路并不复杂，继续往下看，以下是随便勾勒的canvas，其内容像是一个五角星

由于我们需要操作像素点，可以通过ctx.getImageData()拿到整个canvas的所有像素点，再做逐一分析，首先，我们要找到一个起始点，即最小的x坐标，这个点一定是在凸包上的

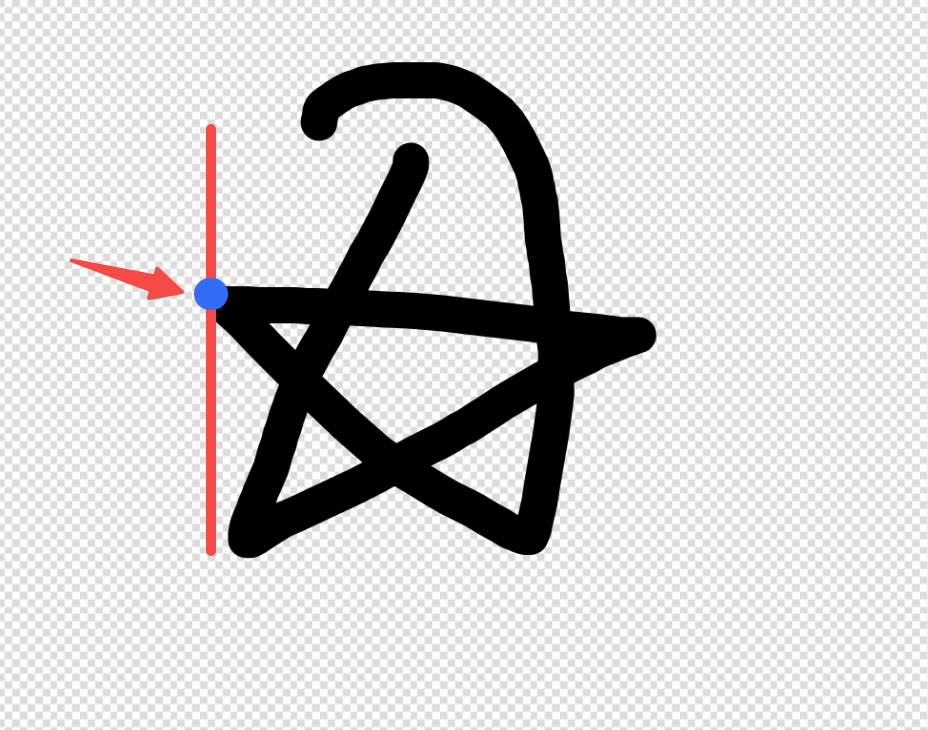
可以通过上到下然后从左到右遍历canvas的imageData，当遇到第一个alpha通道不为0的像素，就是我们要找的起始点，然后我们将它的坐标入栈，继续遍历，找下一个点

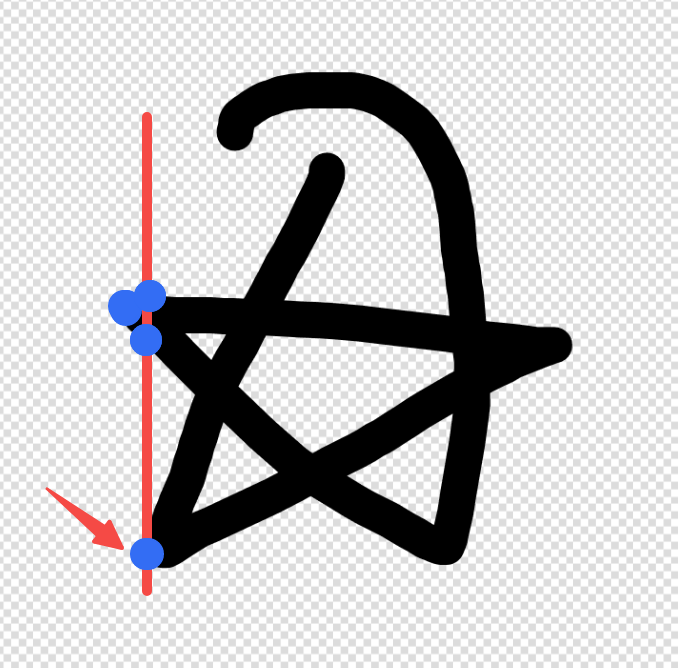
如图所示，我们往右行进一步，其实就是x坐标 +1（现实中像素点是很小的，图中为了方便理解就点的比较大），我们从下往上遍历当前x坐标下y轴上的每个点，就是上图中红线的部分，找到第一个alpha通道不为0的像素，我们把这个像素的坐标入栈，现在我们栈的长度是2，我们以此方法继续行进

如上图，由于没有特殊情况，到这里我们可以一直把点入栈，那什么是特殊情况呢，我们继续往右行进，把图片放大一些方便理解

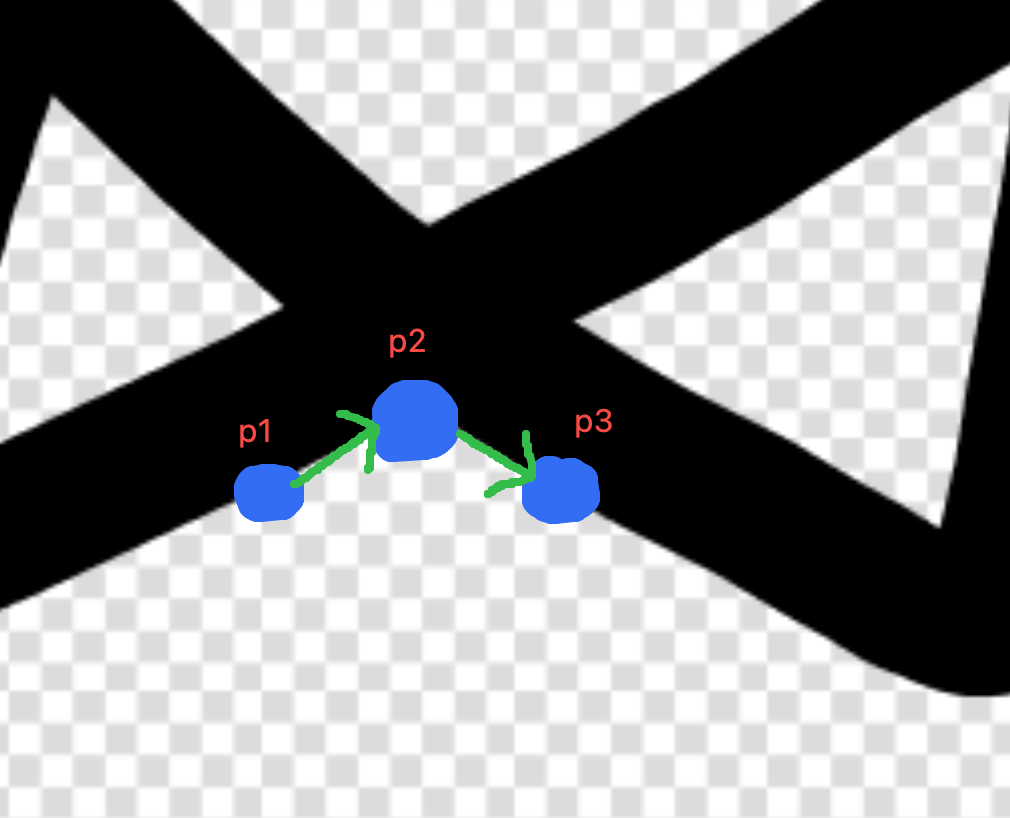
当前我们的栈顶是p2，其前一个元素是p1，将p1 -> p2作为一个向量我们记作prev，下一个点是p3，再将p2 -> p3作为一个向量我们记作next，Andrew算法的核心是，当next向量在prev向量的左侧，我们可以把点p3直接入栈，如果next向量在prev向量的右侧，那栈顶元素(p2)出栈，然后继续以当前栈顶前一个元素(p1的上一个元素)和栈顶元素(p1)组成向量prev，栈顶元素(p1)和p3组成向量next，进行方向比较，如果向量next还是在向量prev的右侧就继续把栈顶元素出栈，继续往前比较，直到比较到是左侧，才将p3入栈，然后才继续向右行进

向量通过终点坐标 – 起始坐标 得到

function create(v1, v2) {
    return {
        x: v2.x - v1.x,
        y: v2.y - v1.y
    };
}

向量方向通过叉乘得到，结果大于0就是右侧

function cross(v1, v2) {
    return v1.x * v2.y - v2.x * v1.y;
}

然后我们按照以上的规则，继续向右进行

由于我们一开始是从下到上，从左到右遍历，所以最终我们得到是4个点形成的一个下凸包区域

之后我们只需要再从上到下，从右到左，将会得到一个上凸包的区域，合并两个凸包数组就是我们要的的凸包拉

最终效果

以上的图都是纯手画的，有点手残，我们看下最终代码的效果

这里在canvas上把计算后凸包的各个点做了ctx.moveTo()连接，并通过ctx.fill()的形式绘制，同时增加了描边的宽度，整体看起来会好看些。