本文介绍: 机器学习(Machine Learning, ML)是一个总称,用于解决由各位程序员自己基于 if-else 等规则开发算法而导致成本过高的问题,想要通过帮助机器 「发现」 它们 「自己」 解决问题的算法来解决 ,而不需要程序员将所有规则都输入机器,明确告诉机器该怎么做。
前言
机器学习(Machine Learning, ML)是一个总称,用于解决由各位程序员自己基于 if-else 等规则开发算法而导致成本过高的问题,想要通过帮助机器 「发现」 它们 「自己」 解决问题的算法来解决 ,而不需要程序员将所有规则都输入机器,明确告诉机器该怎么做。
机器学习概念
机器学习的核心是“使用算法解析数据,从中学习,然后对新数据做出决定或预测”。也就是说计算机利用以获取的数据得出某一模型,然后利用此模型进行预测的一种方法,这个过程跟人的学习过程有些类似,比如人获取一定的经验,可以对新问题进行预测。

可以看到,神经网络只是机器学习中的一部分,除了神经网络,机器学习还有着许多其他的算法。机器学习在多年的发展中逐步丰富,已经被人们开发出了许多中算法
机器学习的分类
机器学习按照学习的方式可以分为
按照工作的方式可以分为
对于算法模型本身分类
机器学习的应用
学习环境
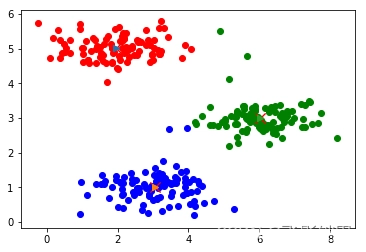
K近邻
学习算法原理
距离的度量
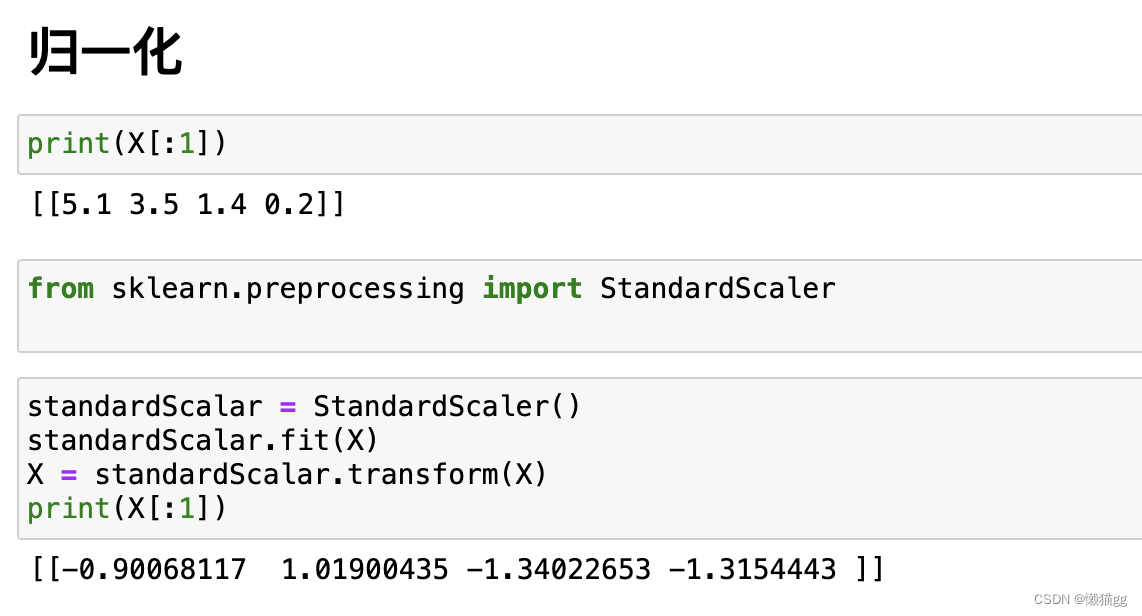
特征归一化
超参数K
流程实施
主要参考
声明:本站所有文章,如无特殊说明或标注,均为本站原创发布。任何个人或组织,在未征得本站同意时,禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益,可联系我们进行处理。