知识回顾:
[1] 生成式建模概述
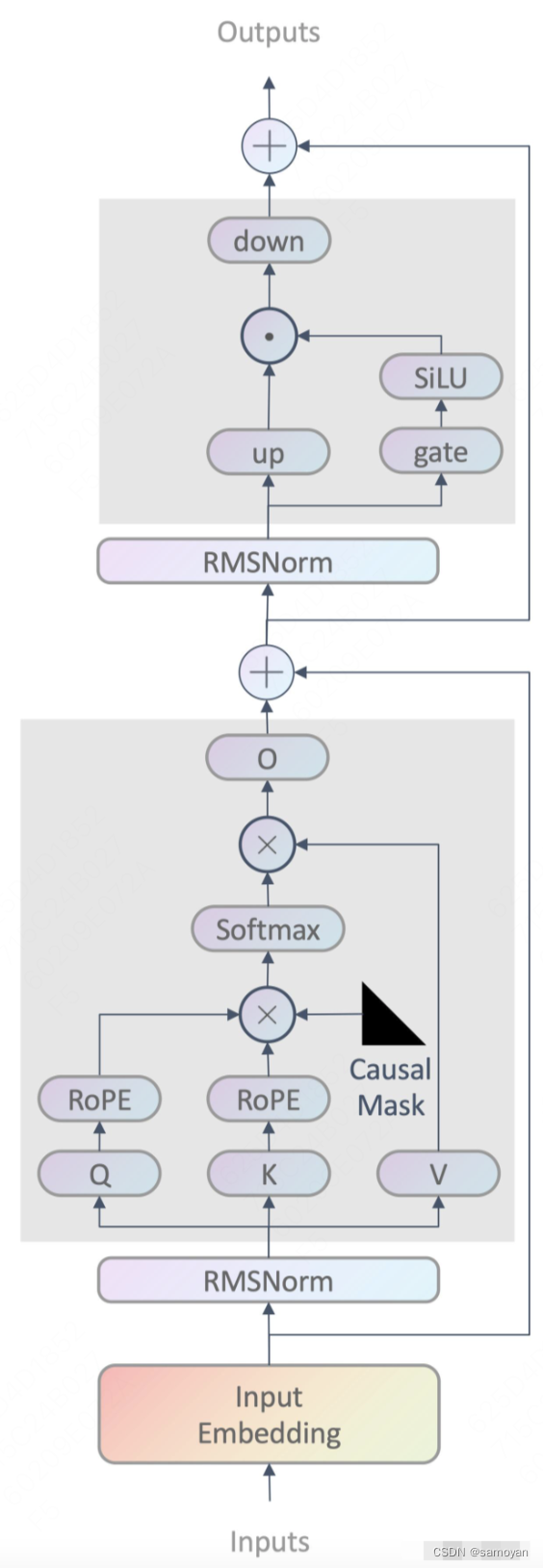
[2] Transformer I,Transformer II
[3] 变分自编码器
[4] 生成对抗网络,高级生成对抗网络 I,高级生成对抗网络 II
[5] 自回归模型
[6] 归一化流模型
[7] 基于能量的模型
[8] 扩散模型 I, 扩散模型 II
引言
去噪扩散概率模型(DDPM)是深度生成模型,最近因其令人印象深刻的性能而受到广泛关注。OpenAI 的DALL-E 2 和 Google 的Imagen生成器等全新模型都基于 DDPM。他们将生成器设置为文本,这样就可以在给定任意文本字符串的情况下生成照片般逼真的图像。
例如,在新的Imagen模型中输入“A photo of a Shiba Inu dog with a backpack riding a bike. It is wearing sunglasses and a beach hat” , DALL-E 2模型中的“a corgi’s head depicted as an explosion of a nebula”,产生以下图像:

这些模型简直令人兴奋,但要了解它们的工作原理,就需要了解 Ho 等人的原创作品。等人。“去噪扩散概率模型”。
在这篇简短的文章中,我将重点介绍(在 PyTorch 中)从头开始创建 DDPM 的简单版本。特别是,我将重新实现Ho 的原始论文。等人。我们将使用经典且不占用资源的 MNIST 和 Fashion-MNIST 数据集,并尝试凭空生成图像。让我们从一些理论开始。
去噪扩散概率模型
这个想法非常简单:给定图像数据集,我们逐步添加一点噪声。每一步,图像都会变得越来越不清晰,直到只剩下噪声。这称为“前向过程”。然后,我们学习一个机器学习模型,可以撤销每个这样的步骤,我们称之为“后向过程”。如果我们能够成功学习后向过程,我们就有了一个可以从纯随机噪声生成图像的模型。

前向过程中的一个步骤是通过从多元高斯分布中采样来使输入图像(步骤 t 处的 x)变得更加嘈杂,该分布的均值是前一图像(步骤 t-1 处的 x)的缩小版本,并且协方差矩阵是对角线且固定。换句话说,我们通过添加一些正态分布值来独立地扰动图像中的每个像素。

对于每个步骤,都有一个不同的系数 beta,它表明我们在该步骤中扭曲图像的程度。beta 越高,图像中添加的噪声就越多。我们可以自由选择系数 beta,但我们应该尽量不要一次性添加太多噪音,并且整体前向过程应该是“平滑”的。在 Ho 等人的原创作品中。beta 被放置在从 0.0001 到 0.02 的线性空间中。
高斯分布的一个很好的特性是,我们可以通过将按标准差缩放的正态分布噪声向量添加到均值向量来从中采样。这导致:

我们现在知道如何通过缩放我们已有的样本并添加一些缩放后的噪声来获得前向过程中的下一个样本。如果我们现在认为该公式是递归的,我们可以写作:

如果我们继续这样做并做一些简化,我们可以一路返回并获得从原始无噪声图像 x0 开始在步骤 t 获取噪声样本的公式:

Great!现在,无论我们的前向过程有多少步,我们总是有办法直接从原始图像中直接获取第 t 步的噪声图像。
对于后向过程,我们知道我们的模型也应该作为高斯分布工作,因此我们只需要模型在给定噪声图像和时间步长的情况下预测分布均值和标准差。实际上,在第一篇关于 DDPM 的论文中,协方差矩阵保持固定,因此我们只想预测高斯的均值(给定噪声图像和当前所处的时间步长):

现在,事实证明,要预测的最佳平均值只是我们已经熟悉的项之函数:

因此,我们可以进一步简化我们的模型,只用噪声图像和时间步长的函数来预测噪声 epsilon。

我们的损失函数只是添加的真实噪声与模型预测的噪声之间均方误差 (MSE) 的缩放版本:

一旦模型训练完成(Algorithm 1),我们就可以使用去噪模型对新图像进行采样(Algorithm 2)。

让我们开始coding
现在我们已经大致了解了扩散模型的工作原理,是时候实现我们自己的一些东西了。您可以在此GitHub 存储库自行运行以下代码。
# Import of libraries
import random
import imageio
import numpy as np
from argparse import ArgumentParser
from tqdm.auto import tqdm
import matplotlib.pyplot as plt
import einops
import torch
import torch.nn as nn
from torch.optim import Adam
from torch.utils.data import DataLoader
from torchvision.transforms import Compose, ToTensor, Lambda
from torchvision.datasets.mnist import MNIST, FashionMNIST
# Setting reproducibility
SEED = 0
random.seed(SEED)
np.random.seed(SEED)
torch.manual_seed(SEED)
# Definitions
STORE_PATH_MNIST = f"ddpm_model_mnist.pt"
STORE_PATH_FASHION = f"ddpm_model_fashion.pt"
接下来,我们为实验定义一些参数。特别是,我们决定是否要运行训练循环,是否要使用 Fashion-MNIST 数据集和一些训练超参数。
no_train = False
fashion = True
batch_size = 128
n_epochs = 20
lr = 0.001
store_path = "ddpm_fashion.pt" if fashion else "ddpm_mnist.pt"
接下来,我们真的很想显示图像。我们对训练图像和模型生成的图像都很感兴趣。我们编写一个实用函数,给定一些图像,将显示子图的正方形(或尽可能接近)网格:
def show_images(images, title=""):
"""Shows the provided images as sub-pictures in a square"""
# Converting images to CPU numpy arrays
if type(images) is torch.Tensor:
images = images.detach().cpu().numpy()
# Defining number of rows and columns
fig = plt.figure(figsize=(8, 8))
rows = int(len(images) ** (1 / 2))
cols = round(len(images) / rows)
# Populating figure with sub-plots
idx = 0
for r in range(rows):
for c in range(cols):
fig.add_subplot(rows, cols, idx + 1)
if idx < len(images):
plt.imshow(images[idx][0], cmap="gray")
idx += 1
fig.suptitle(title, fontsize=30)
# Showing the figure
plt.show()
为了测试这个实用函数,我们加载数据集并显示第一批。重要提示:图像必须在 [-1, 1] 范围内标准化,因为我们的网络必须预测正态分布的噪声值:
# Shows the first batch of images
def show_first_batch(loader):
for batch in loader:
show_images(batch[0], "Images in the first batch")
break
# Loading the data (converting each image into a tensor and normalizing between [-1, 1])
transform = Compose([
ToTensor(),
Lambda(lambda x: (x - 0.5) * 2)]
)
ds_fn = FashionMNIST if fashion else MNIST
dataset = ds_fn("./datasets", download=True, train=True, transform=transform)
loader = DataLoader(dataset, batch_size, shuffle=True)

Great!现在我们有了这个很好的实用函数,稍后我们也将把它用于我们的模型生成的图像。在我们开始实际处理 DDPM 模型之前,我们获取一个 GPU 设备:

DDPM 模型
现在我们已经解决了这些琐碎的事情,是时候处理 DDPM 了。我们将创建一个MyDDPM PyTorch 模块,负责存储 beta 和 alpha 值并应用前向过程。对于后向过程,MyDDPM模块将仅依赖于用于构建 DDPM 的网络:
# DDPM class
class MyDDPM(nn.Module):
def __init__(self, network, n_steps=200, min_beta=10 ** -4, max_beta=0.02, device=None, image_chw=(1, 28, 28)):
super(MyDDPM, self).__init__()
self.n_steps = n_steps
self.device = device
self.image_chw = image_chw
self.network = network.to(device)
self.betas = torch.linspace(min_beta, max_beta, n_steps).to(
device) # Number of steps is typically in the order of thousands
self.alphas = 1 - self.betas
self.alpha_bars = torch.tensor([torch.prod(self.alphas[:i + 1]) for i in range(len(self.alphas))]).to(device)
def forward(self, x0, t, eta=None):
# Make input image more noisy (we can directly skip to the desired step)
n, c, h, w = x0.shape
a_bar = self.alpha_bars[t]
if eta is None:
eta = torch.randn(n, c, h, w).to(self.device)
noisy = a_bar.sqrt().reshape(n, 1, 1, 1) * x0 + (1 - a_bar).sqrt().reshape(n, 1, 1, 1) * eta
return noisy
def backward(self, x, t):
# Run each image through the network for each timestep t in the vector t.
# The network returns its estimation of the noise that was added.
return self.network(x, t)
请注意,前向过程独立于用于去噪的网络,因此从技术上讲,我们已经可以可视化其效果。同时,我们还可以创建一个实用函数,应用Algorithm 2(采样过程)来生成新图像。我们使用两个 DDPM 的特定实用函数来实现此目的:
def show_forward(ddpm, loader, device):
# Showing the forward process
for batch in loader:
imgs = batch[0]
show_images(imgs, "Original images")
for percent in [0.25, 0.5, 0.75, 1]:
show_images(
ddpm(imgs.to(device),
[int(percent * ddpm.n_steps) - 1 for _ in range(len(imgs))]),
f"DDPM Noisy images {int(percent * 100)}%"
)
break
为了生成图像,我们从随机噪声开始,让 t 从 T 回到 0。在每一步,我们将噪声估计为eta_theta并应用去噪函数。最后,如Langevin dynamics一样添加额外的噪声。
def generate_new_images(ddpm, n_samples=16, device=None, frames_per_gif=100, gif_name="sampling.gif", c=1, h=28, w=28):
"""Given a DDPM model, a number of samples to be generated and a device, returns some newly generated samples"""
frame_idxs = np.linspace(0, ddpm.n_steps, frames_per_gif).astype(np.uint)
frames = []
with torch.no_grad():
if device is None:
device = ddpm.device
# Starting from random noise
x = torch.randn(n_samples, c, h, w).to(device)
for idx, t in enumerate(list(range(ddpm.n_steps))[::-1]):
# Estimating noise to be removed
time_tensor = (torch.ones(n_samples, 1) * t).to(device).long()
eta_theta = ddpm.backward(x, time_tensor)
alpha_t = ddpm.alphas[t]
alpha_t_bar = ddpm.alpha_bars[t]
# Partially denoising the image
x = (1 / alpha_t.sqrt()) * (x - (1 - alpha_t) / (1 - alpha_t_bar).sqrt() * eta_theta)
if t > 0:
z = torch.randn(n_samples, c, h, w).to(device)
# Option 1: sigma_t squared = beta_t
beta_t = ddpm.betas[t]
sigma_t = beta_t.sqrt()
# Option 2: sigma_t squared = beta_tilda_t
# prev_alpha_t_bar = ddpm.alpha_bars[t-1] if t > 0 else ddpm.alphas[0]
# beta_tilda_t = ((1 - prev_alpha_t_bar)/(1 - alpha_t_bar)) * beta_t
# sigma_t = beta_tilda_t.sqrt()
# Adding some more noise like in Langevin Dynamics fashion
x = x + sigma_t * z
# Adding frames to the GIF
if idx in frame_idxs or t == 0:
# Putting digits in range [0, 255]
normalized = x.clone()
for i in range(len(normalized)):
normalized[i] -= torch.min(normalized[i])
normalized[i] *= 255 / torch.max(normalized[i])
# Reshaping batch (n, c, h, w) to be a (as much as it gets) square frame
frame = einops.rearrange(normalized, "(b1 b2) c h w -> (b1 h) (b2 w) c", b1=int(n_samples ** 0.5))
frame = frame.cpu().numpy().astype(np.uint8)
# Rendering frame
frames.append(frame)
# Storing the gif
with imageio.get_writer(gif_name, mode="I") as writer:
for idx, frame in enumerate(frames):
writer.append_data(frame)
if idx == len(frames) - 1:
for _ in range(frames_per_gif // 3):
writer.append_data(frames[-1])
return x
与 DDPM 相关的所有内容现在都已摆在桌面上。我们只需要定义一个模型,该模型将在给定图像和当前时间步长的情况下实际完成预测图像中噪声的工作。为此,我们将创建一个自定义 U-Net 模型。不用说,您可以自由选择使用任何其他模型。
U-Net
我们通过创建一个保持空间维度不变的块来开始创建 U-Net。该块将用于我们 U-Net 的各个层次。
class MyBlock(nn.Module):
def __init__(self, shape, in_c, out_c, kernel_size=3, stride=1, padding=1, activation=None, normalize=True):
super(MyBlock, self).__init__()
self.ln = nn.LayerNorm(shape)
self.conv1 = nn.Conv2d(in_c, out_c, kernel_size, stride, padding)
self.conv2 = nn.Conv2d(out_c, out_c, kernel_size, stride, padding)
self.activation = nn.SiLU() if activation is None else activation
self.normalize = normalize
def forward(self, x):
out = self.ln(x) if self.normalize else x
out = self.conv1(out)
out = self.activation(out)
out = self.conv2(out)
out = self.activation(out)
return out
DDPM 中棘手的事情是我们的图像到图像模型必须以当前时间步长为条件。为了在实践中做到这一点,我们使用正弦嵌入和单层 MLP。生成的张量将通过 U-Net 的每个级别按通道添加到网络的输入。
def sinusoidal_embedding(n, d):
# Returns the standard positional embedding
embedding = torch.zeros(n, d)
wk = torch.tensor([1 / 10_000 ** (2 * j / d) for j in range(d)])
wk = wk.reshape((1, d))
t = torch.arange(n).reshape((n, 1))
embedding[:,::2] = torch.sin(t * wk[:,::2])
embedding[:,1::2] = torch.cos(t * wk[:,::2])
return embedding
我们创建一个小的utility函数,用于创建单层 MLP,用于映射位置嵌入。
def _make_te(self, dim_in, dim_out):
return nn.Sequential(
nn.Linear(dim_in, dim_out),
nn.SiLU(),
nn.Linear(dim_out, dim_out)
)
现在我们知道如何处理时间信息,我们可以创建自定义 U-Net 网络。我们将有 3 个下采样部分、网络中间的瓶颈以及 3 个具有通常 U-Net 残差连接(串联)的上采样步骤。
class MyUNet(nn.Module):
def __init__(self, n_steps=1000, time_emb_dim=100):
super(MyUNet, self).__init__()
# Sinusoidal embedding
self.time_embed = nn.Embedding(n_steps, time_emb_dim)
self.time_embed.weight.data = sinusoidal_embedding(n_steps, time_emb_dim)
self.time_embed.requires_grad_(False)
# First half
self.te1 = self._make_te(time_emb_dim, 1)
self.b1 = nn.Sequential(
MyBlock((1, 28, 28), 1, 10),
MyBlock((10, 28, 28), 10, 10),
MyBlock((10, 28, 28), 10, 10)
)
self.down1 = nn.Conv2d(10, 10, 4, 2, 1)
self.te2 = self._make_te(time_emb_dim, 10)
self.b2 = nn.Sequential(
MyBlock((10, 14, 14), 10, 20),
MyBlock((20, 14, 14), 20, 20),
MyBlock((20, 14, 14), 20, 20)
)
self.down2 = nn.Conv2d(20, 20, 4, 2, 1)
self.te3 = self._make_te(time_emb_dim, 20)
self.b3 = nn.Sequential(
MyBlock((20, 7, 7), 20, 40),
MyBlock((40, 7, 7), 40, 40),
MyBlock((40, 7, 7), 40, 40)
)
self.down3 = nn.Sequential(
nn.Conv2d(40, 40, 2, 1),
nn.SiLU(),
nn.Conv2d(40, 40, 4, 2, 1)
)
# Bottleneck
self.te_mid = self._make_te(time_emb_dim, 40)
self.b_mid = nn.Sequential(
MyBlock((40, 3, 3), 40, 20),
MyBlock((20, 3, 3), 20, 20),
MyBlock((20, 3, 3), 20, 40)
)
# Second half
self.up1 = nn.Sequential(
nn.ConvTranspose2d(40, 40, 4, 2, 1),
nn.SiLU(),
nn.ConvTranspose2d(40, 40, 2, 1)
)
self.te4 = self._make_te(time_emb_dim, 80)
self.b4 = nn.Sequential(
MyBlock((80, 7, 7), 80, 40),
MyBlock((40, 7, 7), 40, 20),
MyBlock((20, 7, 7), 20, 20)
)
self.up2 = nn.ConvTranspose2d(20, 20, 4, 2, 1)
self.te5 = self._make_te(time_emb_dim, 40)
self.b5 = nn.Sequential(
MyBlock((40, 14, 14), 40, 20),
MyBlock((20, 14, 14), 20, 10),
MyBlock((10, 14, 14), 10, 10)
)
self.up3 = nn.ConvTranspose2d(10, 10, 4, 2, 1)
self.te_out = self._make_te(time_emb_dim, 20)
self.b_out = nn.Sequential(
MyBlock((20, 28, 28), 20, 10),
MyBlock((10, 28, 28), 10, 10),
MyBlock((10, 28, 28), 10, 10, normalize=False)
)
self.conv_out = nn.Conv2d(10, 1, 3, 1, 1)
def forward(self, x, t):
# x is (N, 2, 28, 28) (image with positional embedding stacked on channel dimension)
t = self.time_embed(t)
n = len(x)
out1 = self.b1(x + self.te1(t).reshape(n, -1, 1, 1)) # (N, 10, 28, 28)
out2 = self.b2(self.down1(out1) + self.te2(t).reshape(n, -1, 1, 1)) # (N, 20, 14, 14)
out3 = self.b3(self.down2(out2) + self.te3(t).reshape(n, -1, 1, 1)) # (N, 40, 7, 7)
out_mid = self.b_mid(self.down3(out3) + self.te_mid(t).reshape(n, -1, 1, 1)) # (N, 40, 3, 3)
out4 = torch.cat((out3, self.up1(out_mid)), dim=1) # (N, 80, 7, 7)
out4 = self.b4(out4 + self.te4(t).reshape(n, -1, 1, 1)) # (N, 20, 7, 7)
out5 = torch.cat((out2, self.up2(out4)), dim=1) # (N, 40, 14, 14)
out5 = self.b5(out5 + self.te5(t).reshape(n, -1, 1, 1)) # (N, 10, 14, 14)
out = torch.cat((out1, self.up3(out5)), dim=1) # (N, 20, 28, 28)
out = self.b_out(out + self.te_out(t).reshape(n, -1, 1, 1)) # (N, 1, 28, 28)
out = self.conv_out(out)
return out
def _make_te(self, dim_in, dim_out):
return nn.Sequential(
nn.Linear(dim_in, dim_out),
nn.SiLU(),
nn.Linear(dim_out, dim_out)
)
现在我们定义了去噪网络,我们可以继续实例化 DDPM 模型并进行一些可视化。
可视化
我们使用自定义 U-Net 实例化 DDPM 模型,如下所示。
# Defining model
n_steps, min_beta, max_beta = 1000, 10 ** -4, 0.02 # Originally used by the authors
ddpm = MyDDPM(MyUNet(n_steps), n_steps=n_steps, min_beta=min_beta, max_beta=max_beta, device=device)
# Optionally, show the diffusion (forward) process
show_forward(ddpm, loader, device)

我们还没有训练模型,但我们已经可以使用允许我们生成新图像的函数并看看会发生什么:

毫不奇怪,当我们这样做时,什么也没有发生。但是,稍后当模型完成训练时,我们将重新使用相同的方法。
Training loop
我们现在实现 Algorithm 1 来学习一个知道如何对图像进行去噪的模型。这对应于我们的Training loop。
def training_loop(ddpm, loader, n_epochs, optim, device, display=False, store_path="ddpm_model.pt"):
mse = nn.MSELoss()
best_loss = float("inf")
n_steps = ddpm.n_steps
for epoch in tqdm(range(n_epochs), desc=f"Training progress", colour="#00ff00"):
epoch_loss = 0.0
for step, batch in enumerate(tqdm(loader, leave=False, desc=f"Epoch {epoch + 1}/{n_epochs}", colour="#005500")):
# Loading data
x0 = batch[0].to(device)
n = len(x0)
# Picking some noise for each of the images in the batch, a timestep and the respective alpha_bars
eta = torch.randn_like(x0).to(device)
t = torch.randint(0, n_steps, (n,)).to(device)
# Computing the noisy image based on x0 and the time-step (forward process)
noisy_imgs = ddpm(x0, t, eta)
# Getting model estimation of noise based on the images and the time-step
eta_theta = ddpm.backward(noisy_imgs, t.reshape(n, -1))
# Optimizing the MSE between the noise plugged and the predicted noise
loss = mse(eta_theta, eta)
optim.zero_grad()
loss.backward()
optim.step()
epoch_loss += loss.item() * len(x0) / len(loader.dataset)
# Display images generated at this epoch
if display:
show_images(generate_new_images(ddpm, device=device), f"Images generated at epoch {epoch + 1}")
log_string = f"Loss at epoch {epoch + 1}: {epoch_loss:.3f}"
# Storing the model
if best_loss > epoch_loss:
best_loss = epoch_loss
torch.save(ddpm.state_dict(), store_path)
log_string += " --> Best model ever (stored)"
print(log_string)
正如您所看到的,在我们的训练循环中,我们只是对一些图像和每个图像的一些随机时间步进行采样。然后,我们通过前向过程使它们变得嘈杂,并对这些嘈杂的图像运行后向过程。实际添加的噪声与模型预测的噪声之间的 MSE 得到优化。

默认情况下,我将训练周期设置为 20,因为每个周期需要 24 秒(总共大约 8 分钟的训练时间)。请注意,通过更多的 epoch、更好的 U-Net 和其他技巧,可以获得更好的性能。在这篇文章中,为了简单起见,我省略了这些内容。
模型测试
现在工作已经完成,我们可以看看成果如何了。我们根据MSE损失函数加载训练时得到的最佳模型,将其设置为评估模式并用它来生成新样本。
# Loading the trained model
best_model = MyDDPM(MyUNet(), n_steps=n_steps, device=device)
best_model.load_state_dict(torch.load(store_path, map_location=device))
best_model.eval()
print("Model loaded")
print("Generating new images")
generated = generate_new_images(
best_model,
n_samples=100,
device=device,
gif_name="fashion.gif" if fashion else "mnist.gif"
)
show_images(generated, "Final result")

锦上添花的是,我们的生成函数会自动创建扩散过程的精美 gif。我们使用以下命令可视化该 gif:

我们完成了!我们的 DDPM 模型终于可以工作了!
进一步改进
已经进行了进一步的改进,以允许生成更高分辨率的图像、加速采样或获得更好的样本质量和似然。Imagen 和 DALL-E 2 模型基于原始 DDPM 的改进版本。
原文地址:https://blog.csdn.net/GarryWang1248/article/details/134658686
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。
如若转载,请注明出处:http://www.7code.cn/show_29146.html
如若内容造成侵权/违法违规/事实不符,请联系代码007邮箱:suwngjj01@126.com进行投诉反馈,一经查实,立即删除!