本文介绍: 整数和浮点数在内存中的存储方式有很大的区别。整数采用固定位数的二进制形式存储,而浮点数采用IEEE 754标准的存储方式。此外,浮点数的表示范围更广,但精度相对较低,而整数的表示范围相对较小,但精度较高。
整数在内存中的存储:
浮点数在内存中的存储:
IEEE 754标准
IEEE 754标准定义了浮点数的存储格式,包括单精度浮点数(32位)和双精度浮点数(64位)。在这两种格式中,浮点数的存储结构都由三个部分组成:符号位、指数位和尾数位。
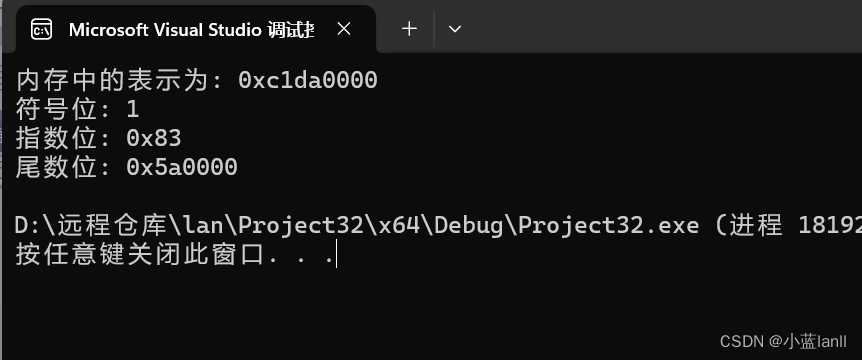
单精度浮点数(32位)
单精度浮点数采用32位来存储,其中1位用于符号位,8位用于指数位,23位用于尾数位。
双精度浮点数(64位)
双精度浮点数采用64位来存储,其中1位用于符号位,11位用于指数位,52位用于尾数位。
特别注意:
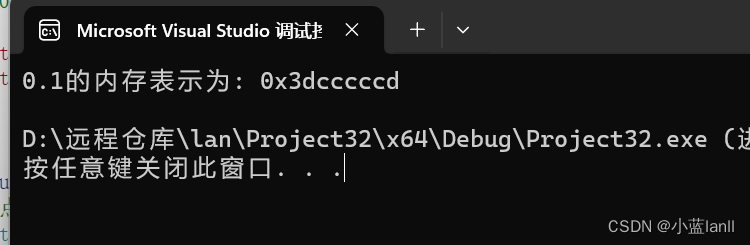
当我们使用单精度浮点数(32位)来存储一个小数时,可能会出现精度丢失的情况。例如,让我们考虑存储十进制数 0.1 在单精度浮点数中的表示。
在十进制中,0.1 可以用有限位数准确表示,但在二进制中,0.1 是一个无限循环小数。因此,在单精度浮点数中,0.1 的精确表示是不可能的。
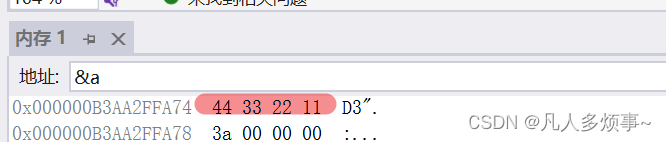
举个例子:
声明:本站所有文章,如无特殊说明或标注,均为本站原创发布。任何个人或组织,在未征得本站同意时,禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益,可联系我们进行处理。