一、说明
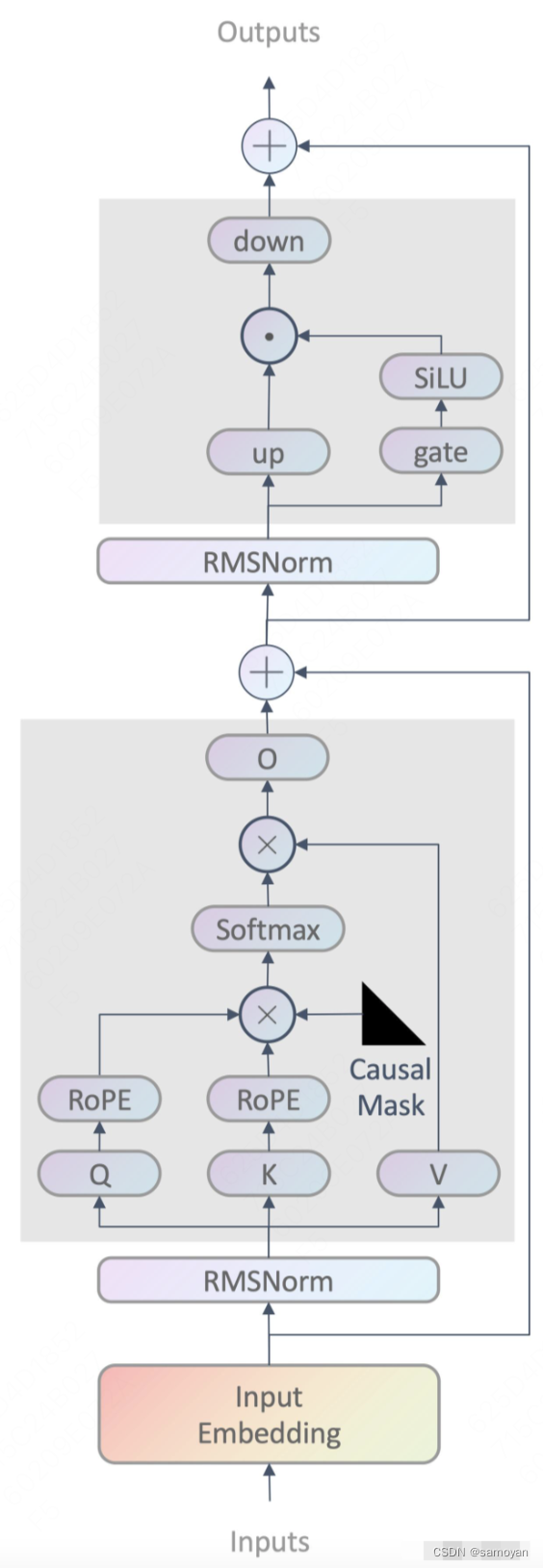
在这篇博客中,我深入研究了将大型语言模型(LLM)提升到基本记忆之上的数学框架。我们探索了动态上下文学习、连续空间插值及其生成能力,揭示了 LLM 如何理解、适应和创新超越传统机器学习模型。
LLM代表了人工智能的重大飞跃,超越了单纯的记忆模型的概念。在第 1 部分中,我介绍了 LLM 如何通过具有语言多样性的更大语料库进行泛化的复杂性。
要详细了解 LLM 的工作原理,您可以在此处找到全面的博客: GPT 背后的巫术

二、动态情境学习与静态映射
2.1 记忆模型:高级有限状态自动机:
数学描述:记忆模型可以使用高级形式的有限状态自动机 (FSA) 表示,该模型可以使用复杂的转移矩阵进行数学建模:
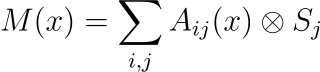
在这个公式中,Aij(x) 是状态转移矩阵的元素,捕获转移概率或规则,而 Sj 是表示自动机中不同状态的状态向量。
固定关系:张量乘积⊗表示状态和输入之间固定的、预先确定的关系。这种刚性与LLM的适应性形成鲜明对比。在语言特征的上下文中,这意味着自动机只能识别和响应它已被明确编程为处理的输入模式。
适应性的局限性:与LLM不同,这些记忆模型缺乏超越其编程状态转换的泛化能力,这使得它们不太擅长处理新颖或看不见的输入模式。
2.2 具有注意力机制的序列到序列建模:
数学基础:LLM,尤其是那些建立在 Transformer 架构上的 LLM,利用了由注意力机制增强的序列到序列模型。这种注意力机制的数学表示如下:
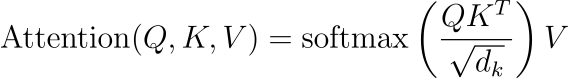
此处,Q、K 和 V 表示从输入数据派生的查询、键和值矩阵。softmax 函数应用于查询和键的缩放点积,确定输出中每个值的权重。
上下文适应:比例因子 dk 对点积进行归一化,以避免由于高维数而导致的超大值。这种归一化在稳定跨层梯度流动方面起着至关重要的作用。
层深度:Transformer 架构中的每一层都应用这种注意力机制,使模型能够对输入序列形成复杂的分层理解。这种多层方法使 LLM 能够捕获数据中细微的关系和依赖关系。
2.3 对比分析:
- 复杂性和灵活性:LLM 具有多层、注意力驱动的架构,与记忆模型中高级 FSA 的静态、基于规则的性质相比,表现出更大程度的复杂性和灵活性。
- 上下文理解:Transformer 的注意力机制允许 LLM 动态权衡和解释输入的不同部分,从而对语言模式有更丰富、更上下文感知的理解。
- 泛化能力:这种动态的情境学习使LLM能够有效地从他们的训练数据中泛化,适应新的场景并产生新的反应,这种能力在记忆模型中受到严重限制。
三、连续空间插值
3.1 记忆模型:具有代数结构的离散映射:
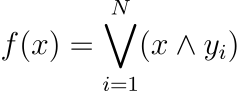
这里,⋁ 表示逻辑 OR 运算,∧ 表示逻辑 AND 运算。每个 yi 都是模型旨在识别的特定模式或状态。
这种表示反映了二进制和确定性映射,其中输出严格由某些输入模式的存在与否来定义。
代数公式的局限性:此类模型受到限制,因为它们无法在显式定义的映射之外进行插值或泛化。该结构是刚性的,这意味着它缺乏灵活性,无法适应与预定义模式不完全匹配的输入。
3.2 LLM:嵌入空间插值:
高维向量空间:基于神经网络的LLM在连续的高维向量空间中运行:
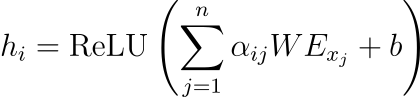
在此公式中,hi 表示上下文中单词或标记的嵌入表示形式。α_ij是注意力权重,W是权重矩阵,E_xj表示第j个标记的嵌入,b是偏置项。
ReLU(整流线性单元)函数引入了非线性,使模型能够捕获数据中的复杂模式。
注意力机制和情境理解:
- 注意力权重 αij 允许模型动态关注输入序列的不同部分。这种机制是理解上下文和单词之间关系的关键。
- 与记忆模型中的离散映射不同,LLM 中基于注意力的插值允许对语言进行细致入微的理解,使模型能够有效地处理歧义、同义词和不同的句子结构。
3.3 比较分析及启示:
- 灵活性和泛化:与记忆模型相比,LLM 表现出显着的灵活性和泛化能力。LLM操作的连续空间允许在含义和上下文中产生细微的变化和渐变,这在记忆模型的离散框架中是不可能的。
- 处理新输入:LLM 擅长处理新输入,根据学习模式进行推理,而不是依赖精确匹配。这与僵化的、基于规则的记忆模型方法形成鲜明对比。
- 复杂模式识别:LLM 中使用的高维向量空间和非线性函数使它们能够捕获和生成复杂的语言模式,由于其二进制和固定性质,这一特征在记忆模型中受到限制。
四、适应性和泛化
4.1 记忆模型:固定概率空间中的随机过程:
随机过程公式:机器学习中的记忆模型可以使用随机过程进行数学表示。一种常见的表示是通过马尔可夫模型,其特征是固定的转移概率:
![]()
这里,st 表示时间 t 的状态,pij 是从状态 i 过渡到状态 j 的概率。这些概率保持不变,反映了模型的静态特性。
固定概率的含义:pij 的恒定性意味着模型的行为是预先确定的,不会根据新的数据或经验而演变。这限制了模型适应新模式或泛化到初始编程之外的能力。
4.2 LLM:梯度下降优化:
梯度下降机制:LLM 采用梯度下降优化,这是现代机器学习的基石。梯度下降更新的基本方程为:
![]()
在这个方程中,θt 表示迭代 t 处的模型参数,η 表示学习率,∇θL(θt;x,y) 是损失函数 L 相对于参数 θ 的梯度。
持续学习和适应:
- 梯度下降的迭代性质允许 LLM 根据从训练数据计算的梯度不断调整和改进其参数。这个过程使模型能够学习复杂的模式,并从其训练数据泛化到新的、看不见的示例。
- 通过ReLU等激活函数引入的非线性进一步增强了LLM的适应性,使它们能够对数据中复杂的非线性关系进行建模。
4.3 对比分析:
静态学习与动态学习:
模式识别的复杂性:
五、复杂模式学习
记忆模型:基于集合理论的局限性:
集合理论表示:机器学习中的记忆模型可以使用集合论进行概念化。模型的知识表示为一组输入-输出对:
![]()
集合 K 中的每个元素都是一对 (xi,yi),其中 xi 是输入,yi 是相应的输出。这个集合是有限和静态的,意味着从输入到输出的固定映射。
静态知识集的含义:
5.1 LLM:使用神经网络层的深度学习:
神经网络层动力学:LLM 使用深度神经网络来捕获复杂的模式。深度神经网络中层的基本方程为:
![]()
这里,h_l+1 是层 l+1 的输出,σ 是非线性激活函数(如 ReLU、sigmoid 或 tanh),Wl 是权重矩阵,bl 是偏置向量,hl 是前一层 l 的输出。
分层学习和泛化:
- 网络的深度(层数)和连接的复杂性(由 Wl 和 bl 定义)允许学习分层特征,从简单到越来越抽象的表示。
- 这种分层学习对于处理自然语言的复杂性至关重要,使 LLM 能够理解和生成细微且上下文丰富的语言。
5.2 对比分析:
- 静态与动态知识表示:记忆模型仅限于静态的、预定义的知识集,而 LLM 通过复杂的神经网络结构动态生成知识。
- 泛化能力:记忆模型中的静态知识表示限制了它们的泛化能力,而 LLM 通过深度学习,擅长从训练数据泛化到新的、看不见的场景。
- 模式的复杂性:LLM 中神经网络的深度和非线性使它们能够捕获比简单的、基于规则的记忆模型方法更复杂的模式。
六、新颖的输出生成:概率建模
作为最后一部分,LLM 使用概率语言模型来生成新颖的输出。核心数学公式以应用于最终隐藏状态的线性变换的 softmax 函数为中心:
![]()
哪里
原文地址:https://blog.csdn.net/gongdiwudu/article/details/134750246
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。
如若转载,请注明出处:http://www.7code.cn/show_29836.html
如若内容造成侵权/违法违规/事实不符,请联系代码007邮箱:suwngjj01@126.com进行投诉反馈,一经查实,立即删除!