神经网络（第三周）

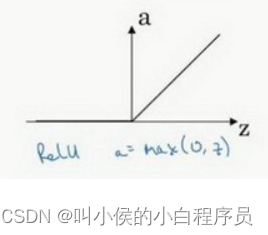
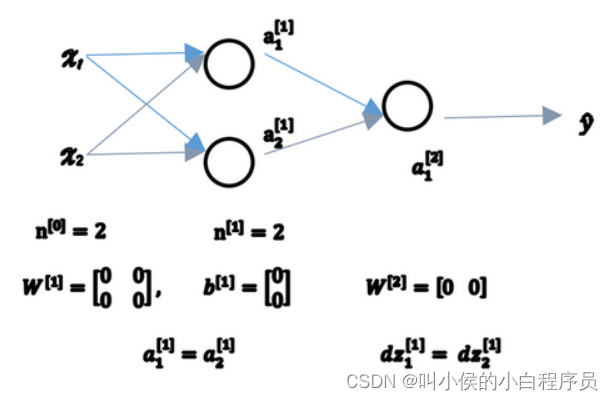
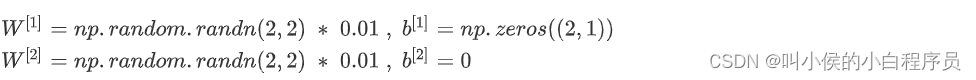本文介绍: 所以，只要是正值的情况下，导数恒等于1，当是负值的时候，导数恒等于0。如果你这样初始化这个神经网络，那么这两个隐含单元就会完全一样，因此他们完全对称，也就意味着计算同样的函数，并且肯定的是最终经过每次训练的迭代，这两个隐含单元仍然是同一个函数。如果你要初始化成0，由于所有的隐含单元都是对称的，无论你运行梯度下降多久，他们一直计算同样的函数，这没有任何帮助。函数两者共同的缺点是：在z特别大或者特别小的情况下，导数的梯度或者函数的斜率会变得特别小，最后就会接近于0，导致梯度下降的速度降低。分析一下这是为什么。

一、简介

1.1 非线性 激活函数

1.1.1 t anh 激活函数

使用一个神经网络时，需要决定在隐藏层上使用哪种激活函数，哪种用在输出层节点上。到目前为止，只用过sigmoid激活函数，但是，有时其他的激活函数效果会更好。t anh函数或者双曲正切函数是总体上都优于sigmoid函数的激活函数。

t anh函数是sigmoid的向下平移和伸缩后的结果。对它进行了变形后，穿过了（0，0）点，并且值域介于+1和-1之间。结果表明，如果在隐藏层上使用tanh函数效果总是优于sigmoid函数。因为函数值域在-1和+1，其均值是更接近零的。在训练一个算法模型时，如果使用tanh函数代替sigmoid函数中心化数据，使得数据的平均值更接近0而不是0.5。这会使下一层学习简单一点！！！

但有一个例外：在二分类的问题中，对于输出层，需要的值是0或1，所以想让数值介于0和1之间，而不是在-1和+1之间，所以需要使用sigmoid激活函数。这种情况下，可以对隐藏层使用tanh激活函数，输出层使用sigmoid函数。

在不同的神经网络层中，激活函数可以不同。

sigmoid函数和tanh函数两者共同的缺点是：在z特别大或者特别小的情况下，导数的梯度或者函数的斜率会变得特别小，最后就会接近于0，导致梯度下降的速度降低。

1.1.2 Relu激活函数

在机器学习中另一个很流行的函数是：修正线性单元的函数（ReLu）。所以，只要是正值的情况下，导数恒等于1，当是负值的时候，导数恒等于0。但是从实际上来说，当使用的导数时，z=0的导数是没有定义的。但是当编程实现的时候，不需要担心这个值，z=0的时候，假设导数是1或者0效果都可以。

Relu的一个缺点是：当z是负值的时候，导数等于0。

1.1.3 Le a k y Relu激活函数

这里也有另一个版本的Relu被称为Le a k y Relu。当是负值时，这个函数的值不是等于0，而是轻微的倾斜，如图。这个函数通常比Relu激活函数效果要好，但是在实际中Leak y ReLu使用的并不多

两者的优点是：

在z的区间变动很大的情况下，激活函数的导数或者激活函数的斜率都会远大于0，在程序实现就是一个if-else语句，而sigmoid函数需要进行浮点四则运算，在实践中，使用ReLu激活函数神经网络通常会比使用sigmoid或者tanh激活函数学习的更快。
sig m o id和tanh函数的导数在正负饱和区的梯度都会接近于0，这会造成梯度弥散，而Relu和Leak y ReLu函数大于0部分都为常数，不会产生梯度弥散现象。(同时应该注意到的是，Relu进入负半区的时候，梯度为0，神经元此时不会训练，产生所谓的稀疏性，而Leaky ReLu不会有这问题)
在ReLu 中，z的梯度一半都是0，但是，有足够的隐藏层使得z值大于0，所以对大多数的训练数据来说学习过程仍然可以很快。

1.2 不同激活函数的使用场合

快速概括一下不同激活函数的过程和结论。

sig m o id激活函数：若是一个二分类问题，除了在输出层使用，其他基本不会用它。
tanh激活函数：tanh是非常优秀的，几乎适合所有场合。
ReLu激活函数：最常用的默认函数，如果不确定用哪个激活函数，就使用ReLu或者Leaky ReLu。公式中max{0.01z，z} 为什么是常数0.01？当然，可以为学习算法选择不同的参数！！！

二、计算

2.1 随机 初始化

当训练神经网络时，权重初始化是很重要的。对于逻辑回归，把权重初始化为0当然是可以的。但是对于一个神经网络，如果你把权重或者参数都初始化为0，那么梯度下降将不会起作用。

分析一下这是为什么。假设有两个输入特征，2个隐藏层单元。因此与第一个隐藏层相关的矩阵，是2*2的矩阵，假设把它初始化为0的2*2矩阵，也等于。（偏置项b初始化为0是合理的，但是把权重初始化为0就有问题了）。如果按照这样初始化的话，你总是会发现和相等，两个激活单元就会一样。因为第一个隐藏层的两个神经元计算同样的函数，当你做反向传播计算时，这会导致和也会一样。

如果你这样初始化这个神经网络，那么这两个隐含单元就会完全一样，因此他们完全对称，也就意味着计算同样的函数，并且肯定的是最终经过每次训练的迭代，这两个隐含单元仍然是同一个函数。dW会是一个这样的矩阵，每一行有同样的值。

由此可以推导，如果你把权重都初始化为0，那么由于隐含单元开始计算同一个函数，所有的隐含单元就会对输出单元有同样的影响。一次迭代后同样的表达式结果仍然是相同的，即隐含单元仍是对称的。通过推导，两次、三次、无论多少次迭代，不管你训练网络多长时间，隐含单元仍然计算的是同样的函数。因此这种情况下再多的隐含单元也没什么意义，因为他们计算同样的东西。

如果你要初始化成0，由于所有的隐含单元都是对称的，无论你运行梯度下降多久，他们一直计算同样的函数，这没有任何帮助。这个问题的解决方法就是随机初始化参数。

把W[1]设为np.random.randn(2,2)(生成（2，2）高斯分布)，通常再乘上一个小的数，比如0.01，这样把权重初始化为很小的随机数。b没有对称的问题（叫做symmetry break in g problem），所以可以把 b初始化为0。只要随机初始化权重你就有不同的隐含单元计算不同的东西，因此不会有sym metry break in g问题了。相似的，你可以随机初始化W[2]，初始化b为0。

你也许会疑惑，这个常数从哪里来，为什么是0.01，而不是100或者1000。我们通常倾向于初始化为很小的随机数。因为如果你用tanh或者sigmo id激活函数，或者说只在输出层有一个Si gm o id，如果（数值）波动太大，这种情况下你很可能停在tanh/sigmo id函数的平坦的地方，这些地方梯度很小也就意味着梯度下降会很慢，因此学习也就很慢。

W如果很大，那么你很可能最终停在（甚至在训练刚刚开始的时候）很大的值。如果在你整个的神经网络里没有sigmo id/tanh激活函数，就不成问题。但如果你做二分类并且你的输出单元是Sigm o id函数，那么初始参数就不能太大，因此这就是为什么乘上0.01或者其他一些小数的原因。