《opencv实用探索·八》图像模糊之均值滤波简单理解

本文介绍: 这里需要注意的是在二维高斯函数中标准差σ只有一种，没有σ1和σ2，如果我们设置 sig m aX等于sig m aY,这样拿到的是一个圆形高斯核完全和二维高斯函数生成的一样，如果sigmaX不等于sigmaY我们拿到的是一个椭圆形高斯核，即在X和Y方向调用了分别调用二维高斯函数计算高斯核，因为标准差σ不一样。这种“格格不入”的像素就被称为图像的噪声。在图像处理中，为了提升图像的整体质量，通常我们需要对图像进行模糊处理，即通过卷积运算对每个像素进行滤波或平滑，减少图像的细节，使得图像噪声削弱，凸显特征明显的区域。

1、前言
什么是噪声？
该像素与周围像素的差别非常大，导致从视觉上就能看出该像素无法与周围像素组成可识别的图像信息，降低了整个图像的质量。这种“格格不入”的像素就被称为图像的噪声。如果图像中的噪声都是随机的纯黑像素或者纯白像素，这样的噪声也被称为“椒盐噪声”或“盐噪声”。

在图像处理中，为了提升图像的整体质量，通常我们需要对图像进行模糊处理，即通过卷积运算对每个像素进行滤波或平滑，减少图像的细节，使得图像噪声削弱，凸显特征明显的区域。图像的卷积运算上一章已介绍，这里不再赘述。

2、均值滤波
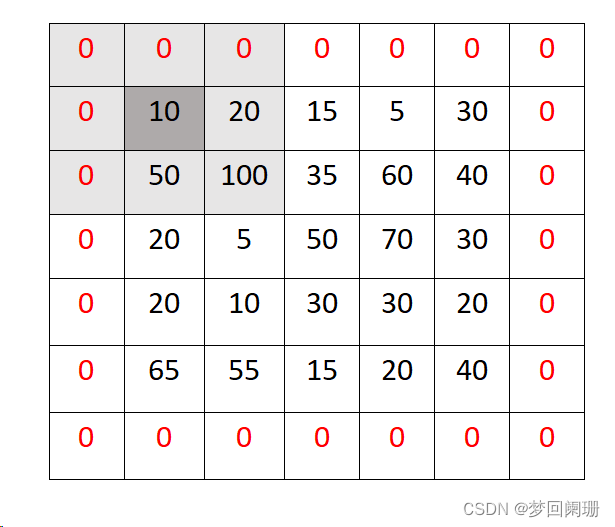
把卷积核覆盖在原图上上依次滑过每个像素，计算卷积核覆盖像素值的加权平均并赋值给被核中心覆盖的那个像素值。比如下图原图像是一个5x5图像，现在有个3×3卷积核，放在图像最开始的位置，计算卷积核覆盖的像素值的加权平均：
注意：均值滤波卷积核上的每个权重默认为1
卷积核：
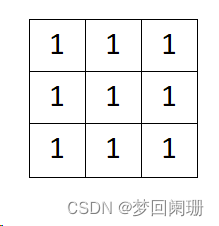
在这里插入图片描述
原图像：

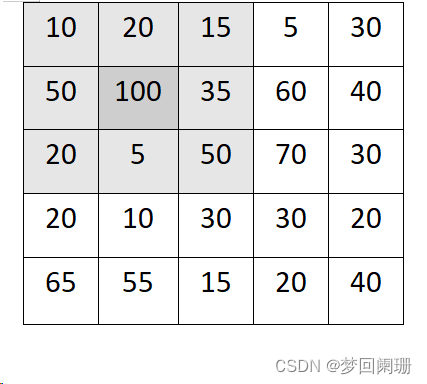
加权平均计算：

(10+20+15+50+100+35+20+5+50)* 1 / (1+1+1+1+1+1+1+1+1) = 33

核中心像素值，即原图像第二行第二列会被重新赋值为33
下图阴影区域为核中心滑过的区域：
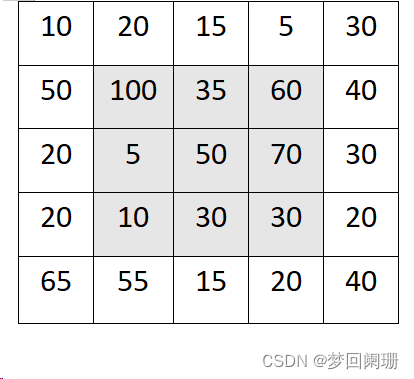
在这里插入图片描述
可以看到原图像5×5，在经过卷积运算后图像变为了3×3，如果想让核中心扫过图像边缘像素，保持图像大小不变，可以在原图像基础上拓展一层边缘，如下图：

opencv提供了均值滤波接口如下：

void cv::blur(InputArray src, OutputArray dst, Size ksize, Point anchor=Point(-1,-1), int borderType=BORDER_DEFAULT)

src：原图
 dst：滤波后图像
k size：卷积核大小，注意卷积核只能是奇数，这样才有核中心，建议使用3×3，5×5和7×7，卷积核越大图像越模糊，卷积时间越长
anc h o r ：表示锚点(ancho r)的位置，即被平滑的那个点。默认值Po int(-1,-1)表示锚点位于核的中心。
borderTy pe：边框模式用于推断图像外部的像素（一般默认）

我们现在用5×5卷积核对下列图像做均值滤波，可以看到右边图像已模糊处理：
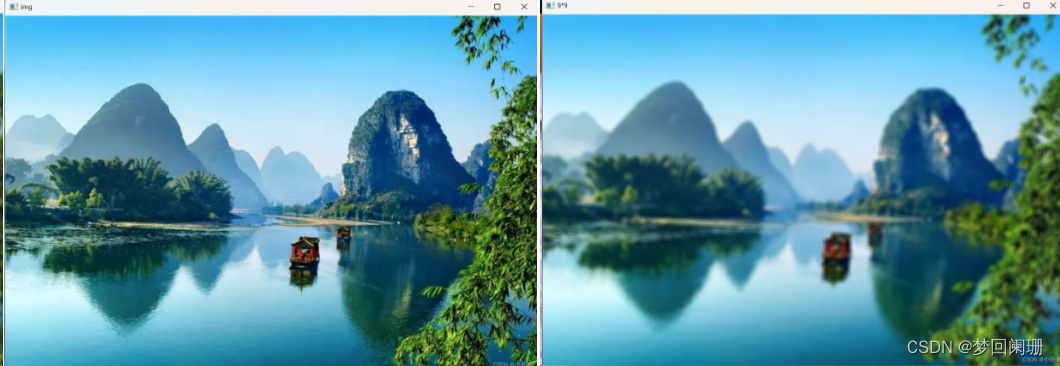
在这里插入图片描述
由于均值模糊是对窗口中所有像素点求平均值，在图像的边缘或者纹理丰富的地方也会变得模糊。为了尽可能的保留图像中的边缘信息，可以给不同位置的像素点赋以不同的权值。距离中心点越近的像素，权值越大，而远离中心点的像素，权值也逐渐减少，这时候可以采用高斯滤波。

3、高斯滤波

在高斯滤波中卷积核的权重由高斯分布（正态分布）的取值来确定。
我们首先来介绍下高斯函数。

一维高斯函数：
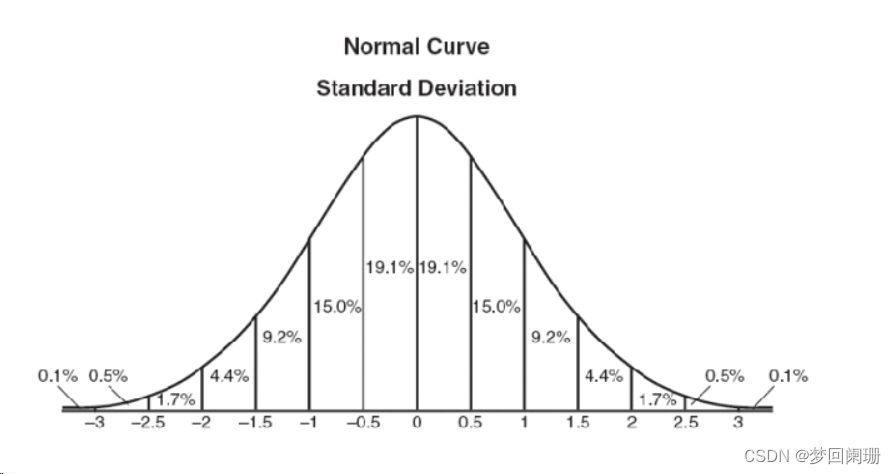
从下图中可以看到高斯分布（正态分布）是一种钟形曲线，越接近中心，取值越大，越远离中心，取值越小。我们给卷积核分配权重的时候，以曲线中心点为原点分配给核中心，核其他位置的权重按高斯曲线上递减趋势分配。
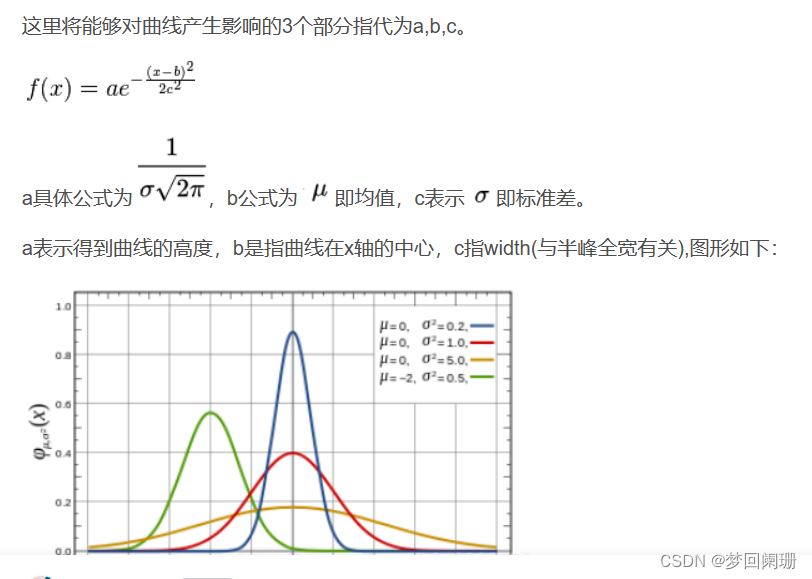
高斯函数中的参数σ表征着高斯滤波器宽度(决定着平滑程度)，当σ越大，高斯滤波器的频带就越宽，平滑程度就越高(越接近均值滤波)．通过调节平滑程度参数σ，可调整图像的平滑程度。
在这里插入图片描述

概率密度函数也为高斯函数。因为该函数只有一个变量x，所以我们也称该函数为一维高斯函数。

再回到一维高斯函数图中，图中X轴的数值表示标准差的大小，比如0.5表示0.5个标准差大小，对应的高斯曲线上面的数值为0.5sigma，在0-0.5sigma区间内占比为19.1%。当我们取-3sigma-3si gma区间，占比达到99.8%，默认该段分布包含了所有情况。

二维高斯函数：
因为图像是二维空间，涉及XY两个方向，这时候用一维高斯函数进行处理显然不太合适，这时引入二维高斯函数是一个很好的解决方案。
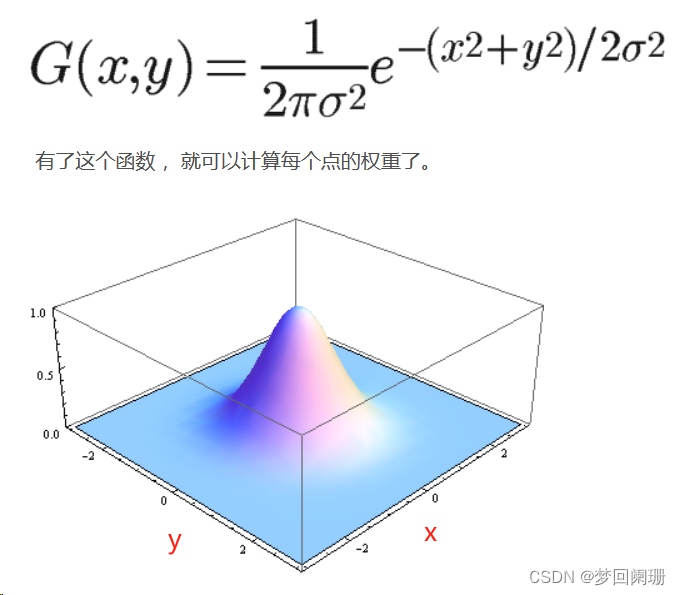
在这里插入图片描述

引入二维高斯函数进行模糊处理：

假设一个高斯函数的卷积和模板是5*5，那么他这25个点的x，y具体取值为：
在这里插入图片描述
此时只需要假定一个 si gma值，即可确定一个高斯核，比如：

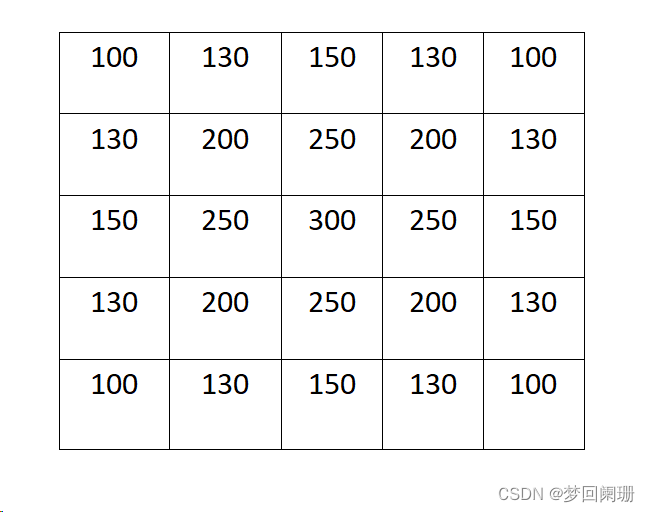
但是这个高斯核不完整，因为他求出的5*5的卷积核进行卷积操作时，改变了图像原始的0-255的范围。为解决该问题只需要将卷积核归一化即可，即需要保证权重之和等于1，也就是卷积核中每一个值除以卷积的总和。
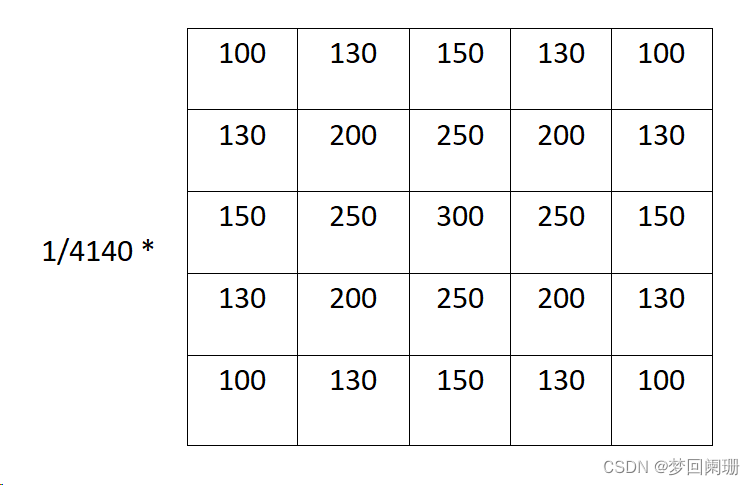
具体的高斯核例如：
实际应用：
有个3×3高斯核，内部坐标如下：
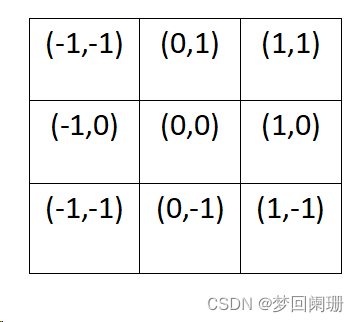
在这里插入图片描述
为了计算权重矩阵，需要设定标准差σ的值。假定σ=1.5，带入二阶高斯函数计算结果如下：

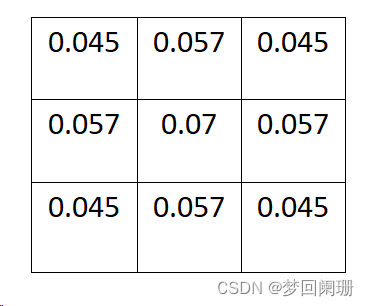
这9个点的权重总和等于0.479，如果只计算这9个点的加权平均，还必须让它们的权重之和等于1，因此上面9个值还要分别除以0.479，得到最终的权重矩阵。
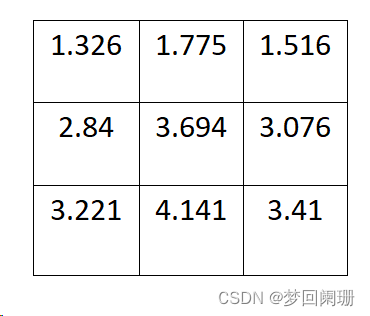
在这里插入图片描述
现在有了高斯核，可以进行图像模糊计算，假设现有9个像素点，灰度值（0-255）如下：

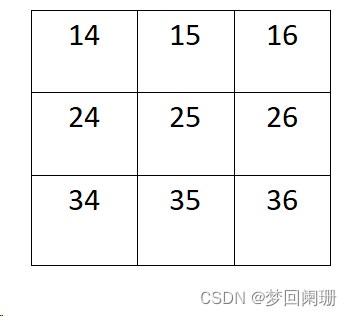
将高斯核覆盖在图像上，覆盖的每个像素点乘以对应的权重再除以权重之和即可得到高斯核中心覆盖的原图像像素最新的值

(1.326*14 + 1.775*15 + 1.516*16 + 2.84*24 + 3.694*25 + 3.076*26 + 3.221*34 + 4.141*35 + 3.41*36) / 1 = 3.694

如果图像很大，将高斯核依次在图像上的每个像素点滑动，计算核中心的像素值，最后就得到了高斯模糊后的图像。如果是彩色图像可对RGB三通道分别进行高斯模糊计算。

opencv高斯模糊函数调用：

void GaussianBlur(
InputArray src,
OutputArray dst,
Size ksize,
double sigmaX,
double sigmaY = 0,
int borderType = BORDER_DEFAULT
);

s rc：原图像
d st：高斯滤波后的图像
k size：滤波核的大小，宽、高必须是奇数，例如（3,3）、（5,5）等。
si gmaX：卷积核水平方向的标准差σ
si gmaY：卷积核垂直方向的标准差σ。修改 si gmaX 或 sigmaY 的值都可以改变卷积核中的权重比例。如果不知道如何设计这两个参数值，就直接把这两个参数的值写成0，方法就会根据滤波核的大小自动计算出合适的权重比例。
boderTyp e：可选参数，边界样式，建议使用默认值。
这里需要注意的是在二维高斯函数中标准差σ只有一种，没有σ1和σ2，如果我们设置 s igmaX等于s igmaY,这样拿到的是一个圆形高斯核完全和二维高斯函数生成的一样，如果sigmaX不等于sigmaY我们拿到的是一个椭圆形高斯核，即在X和Y方向调用了分别调用二维高斯函数计算高斯核，因为标准差σ不一样。
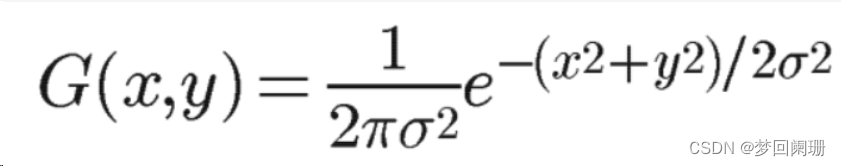
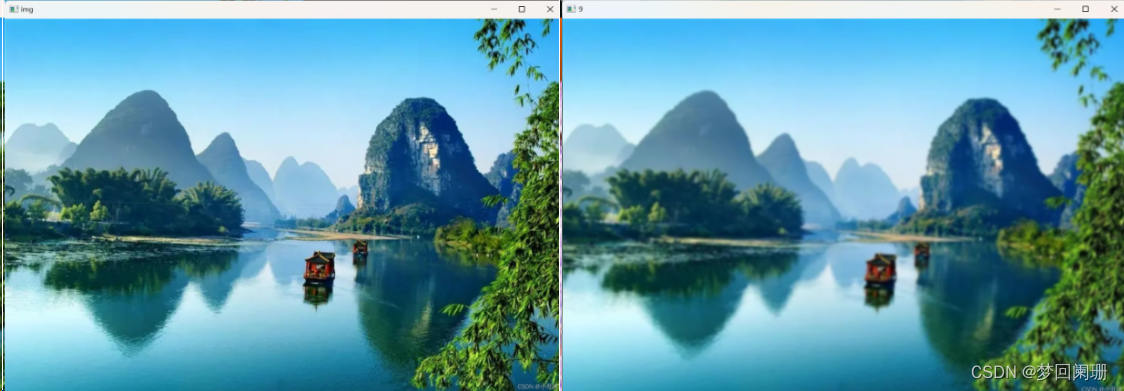
在这里插入图片描述