数学建模-基于BL回归模型和决策树模型对早产危险因素的探究和预测

整体求解过程概述(摘要)

  近年来，全球早产率总体呈上升趋势，在我国，早产儿以每年 20 万的数目逐年递增，目前早产已经成为重大的公共卫生问题之一。据研究,早产是威胁胎儿及新生儿健康的重要因素，可能会造成死亡或智力体力缺陷，因此研究早产的影响因素，建立预测早产的模型就显得极为重要。我们以问卷、面对面访谈的方式，收录了湖南省妇幼保健院 2013 年 5 月 13 日-2019 年 12 月 31 日妊娠 8-14周且接受首次产前护理的孕妇，共 18527 份样本，调查研究孕妇包括医学和社会学信息在内的 104 个变量。基于大样本、多变量的数据特征，对数据预处理后，首先基于传统的统计方法，依次通过 SMOTE 过采样均衡数据、x2 相似性检验剔除无关变量、二阶聚类（TwoStep Cluster）实现降维，用 Binary Logistic 建立早产预测模型，并通过 AUC-ROC 曲线对早产预测模型进行准确性检验；在此基础上，进一步探讨并合理利用机器学习的效力，用数据挖掘的方法，依次通过随机欠抽样平衡样本，特征选择变量实现变量降维，分别用决策树 C5.0 算法，推理集 C5.0算法，决策树 CHAID 算法建立早产预测模型，并通过 boosting 技术提高模型稳健性。
  根据二阶聚类降维结果、Binary Logistic 建立的早产预测模型及检验结果，发现城乡分组、人均月收入、母亲孕前 BMI 分组、受精方式、受孕方式、孕次分组、孕早期柯萨奇病毒、孕前既往性病史、是否采用剖宫产、配偶 BMI 分组这 10 个变量与是否早产的相关性较强，且在经过哑变量处理后，适用于建立早产预测模型。通过 AUC-ROC 曲线，检验出该早产预测模型拟合度良好。在初步探索之后，进一步深入利用机器学习，即分别使用决策树 C5.0 算法，推理集 C5.0 算法，决策树 CHAID 算法建立三个早产预测模型。其中通过决策树 C5.0 算法建立的早产预测模型，在测试集上的准确性为 93.78%，平均正确性为 0.859、平均不正确性为 0.692；推理集 C5.0 算法的准确性为 95.92%，平均正确性为 0.824、平均不正确性为0.714；决策树 CHAID 算法建立的早产预测模型，在测试集上的准确性为79.58%，取置信度为 0.812。

数据预处理

  （一）变量预处理
  类别化处理及选择：将品质变量整理成 0-1 型数值变量，如民族；对于连续变量和其他可合并的变量进行整合，这样会得到有重复信息的变量，比如配偶BMI 值和配偶 BMI 值分组，受孕方式和受孕方式两分类。不做特别说明的情况下，本次研究将主要使用分类型变量，且选择使用分类型变量中分组较少的那一个，比如刚刚提到两组变量，均选择后一组变量进入样本。这是因为在本次研究中，分类型变量占绝大多数，而相同的数据类型有更方便建模的处理，投入到未来实际预测操作中也更加简单明了。
  （二）样本处理
  类别不平衡（class–imbalance）：指分类任务中不同类别的训练样例数目差别很大的情况。在分类学习中方法，默认不同类别的训练样例数目基本相当。若样本类别数目差别很大，属于极端不均衡，会对学习过程（模型训练）造成困扰。这些学习算法的设计背后隐含的优化目标是数据集上的分类准确度，而这会导致学习算法在不平衡数据上更偏向于含更多样本的多数类。多数不平衡学习（imbalance learning）算法就是为解决这种“对多数类的偏好”而提出的。据实践经验表明，正负类样本类别不平衡比例超过 4:1 时，分类要求会因为数据不平衡而无法得到满足，分类器处理结果将变差，导致预测效果达不到预期要求。在本次研究项目中，早产 0:1 比约为 5:1（0 为不发生，1 为发生。本论文其他部分未做其他说明时，都按照该标签规则），因此在构建模型之前，需要对该分类不均衡性问题进行处理。

二阶聚类

  实现步骤
  步骤 1、建立树根 clusterfeature,树根在一开始每个节点中会放置一个数据集中的第一个记录，它就包含有这个数据存储集中每个变量的信息。相似性用的是距离数值测量，数据的相似性可以作为进行距离数值测量的主要标准。相似度高的变量位于同一节点，同时，相似度低的变量生成新节点。似然归类测度模型假设每个变量必须服从特定的概率分布，聚类模型要求分类型独立变量必须服从多项式概率分布，数值型独立变量必须服从正态概率分布。
  步骤 2、合并聚类算法。生成的聚类方案具有不同聚类数，不同的聚类数是基于合并聚类算法下节点的组合成果。
  步骤 3、选择最优聚类数。通过 BIC：Bayesian Information Criterion 准则对各聚类情况进行比较，选出最优聚类方案。
  数值说明
  ①对数似然：这种度量方式用于研究某种以确定概率分布的独立变量。其中数值型变量服从正态分布，分类型变量服从多项式分布。
  ②Bayesian 信息准则( BIC)：在只有部分信息时，要预测未知状态下的部分信息值，选用主观概率；修正发生概率时采用贝叶斯公式，将得到的修正概率与预期产出的值结合计算出最优决策。
  计算公式：
                BIC=ln(n)k–2ln(L)
  其中：k 为模型参数个数；n 为样本数量；L 为似然函数
  聚类结果
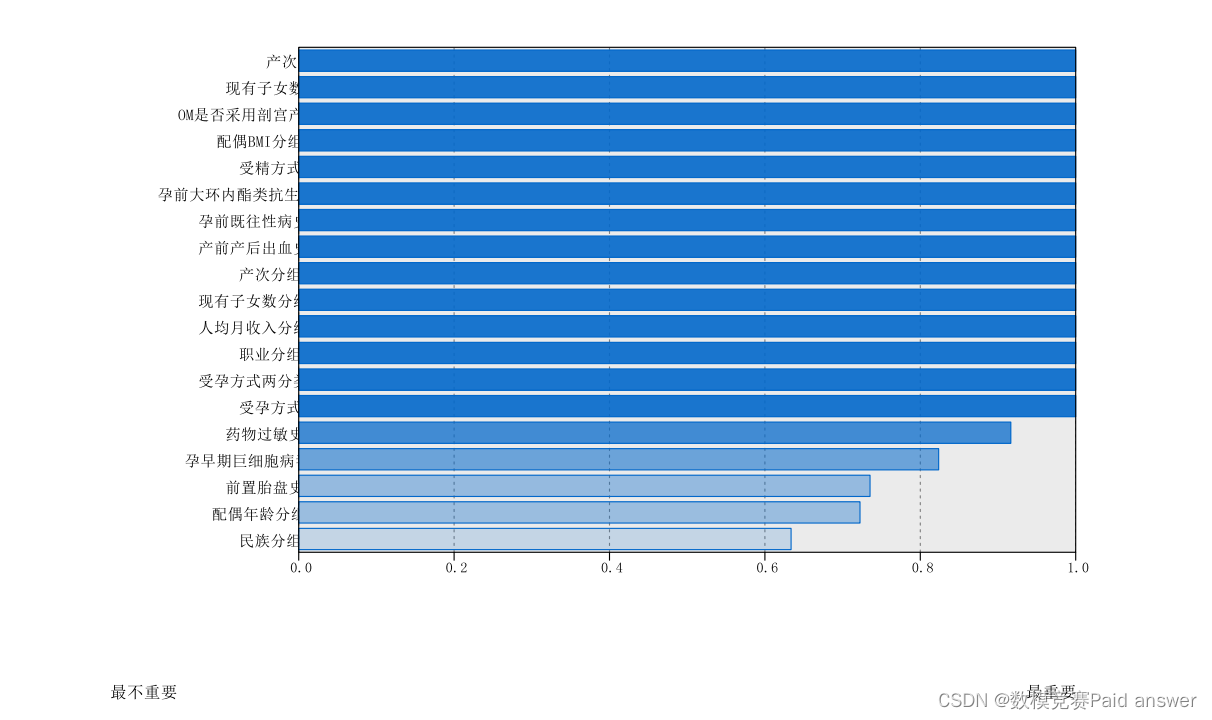
  二阶聚类适用于多分类变量的降维问题。显然，本次研究数据可选用 SPSS 中的二阶聚类对变量进行降维，聚类效果为良好，并最终由 77 个自变量降维到 14个主要变量(该 14 个变量重要性都为 1)

模型的建立与求解整体论文缩略图

全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可

程序代码：(代码和文档not free)

from imblearn.over_sampling import SMOTE
import numpy as np
from sklearn.model_selection import train_test_split
data = pd.read_excel('1(2).xlsx') #读取数据集
data = data.dropna(axis = 1, how = 'any') # 丢弃有 NAN 的列
data = data.dropna(axis = 0, how = 'any') # 丢弃有 NAN 的行
data = data.drop(columns=['ID', '调查人署名']) # 丢弃 ID 和调查人属名，这两
个非 float，放在这里是无效的
var = data.columns
Y = data.iloc[:,-1] # 获得因变量数据
X = data.iloc[:,:-1] # 获得自变量数据
oversampler=SMOTE(random_state=2021) # 导入过采样库—SMOTE 算法
# x_train, x_valid_test, y_train, y_valid_test = 
train_test_split(X,Y,test_size=0.3,random_state=2020) # 将数据集切分为 训练集和
验证+测试集
x_train,y_train=oversampler.fit_sample(X,Y) # 对训练集进行 SMOTE 过采样，
得到过采样后的自变量和因变量
# 
x_valid,x_test,y_valid,y_test=train_test_split(x_valid_test,y_valid_test,test_size=0.3,r
andom_state=2020)
data_smote = pd.concat([x_train,y_train],axis = 1)

全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可

代码007普通

打赏 收藏 海报 链接