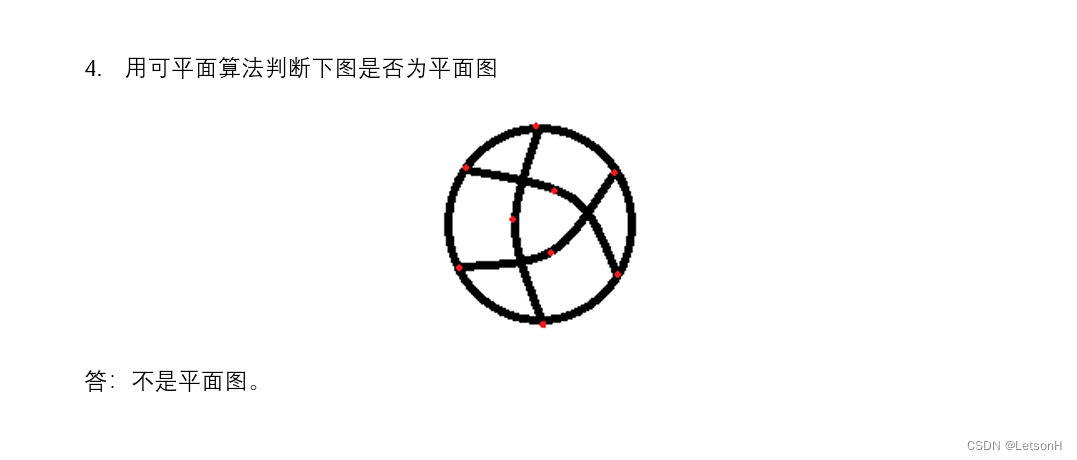
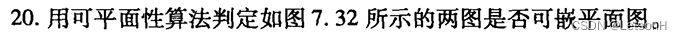考试章节范围


第一章:1.1、1.2、1.3
填空
作业






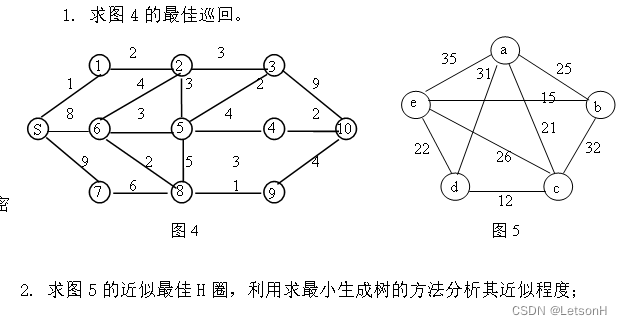
第二章:2.1、2.4、2.5
填空
计算
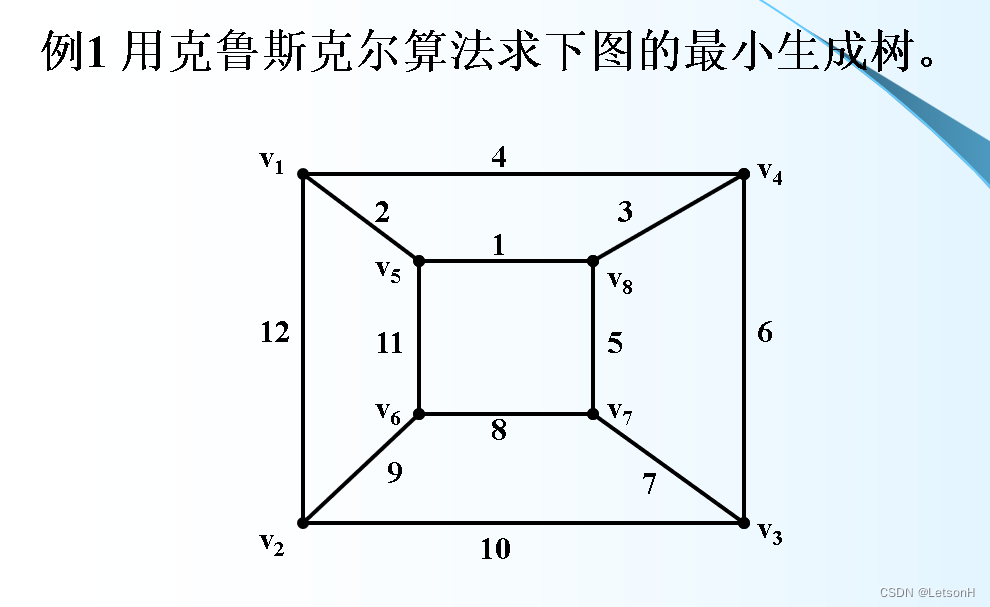

作业
第三章:3.1、3.2
填空
作业
第四章:4.1
计算
作业
第五章:5.1、5.2、5.3、5.4
填空
计算
作业
第六章:6.1、6.2、6.5、6.8、6.9
填空
计算
作业
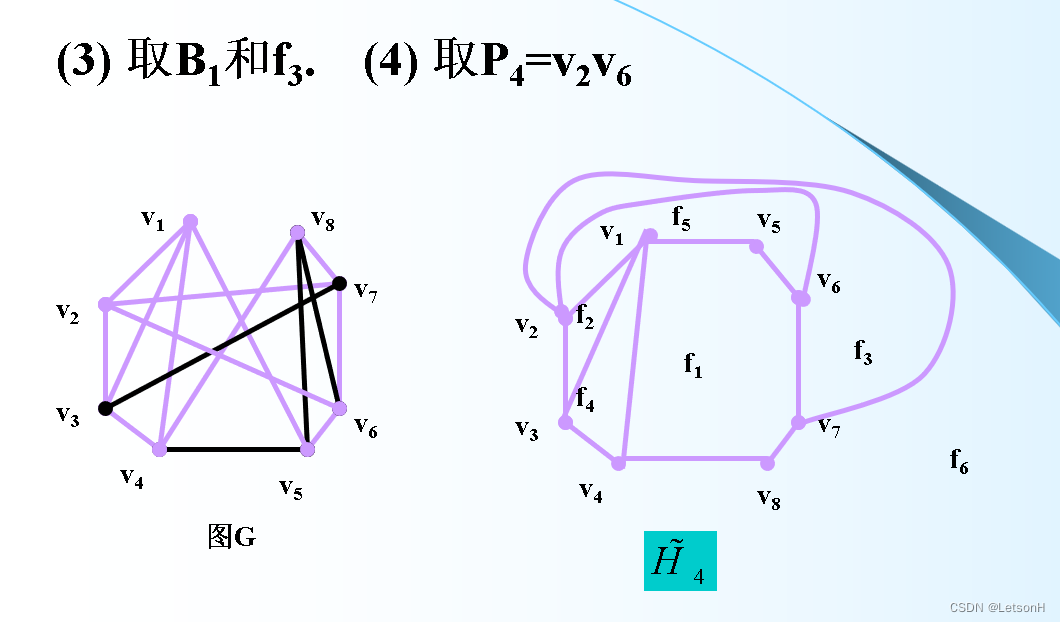
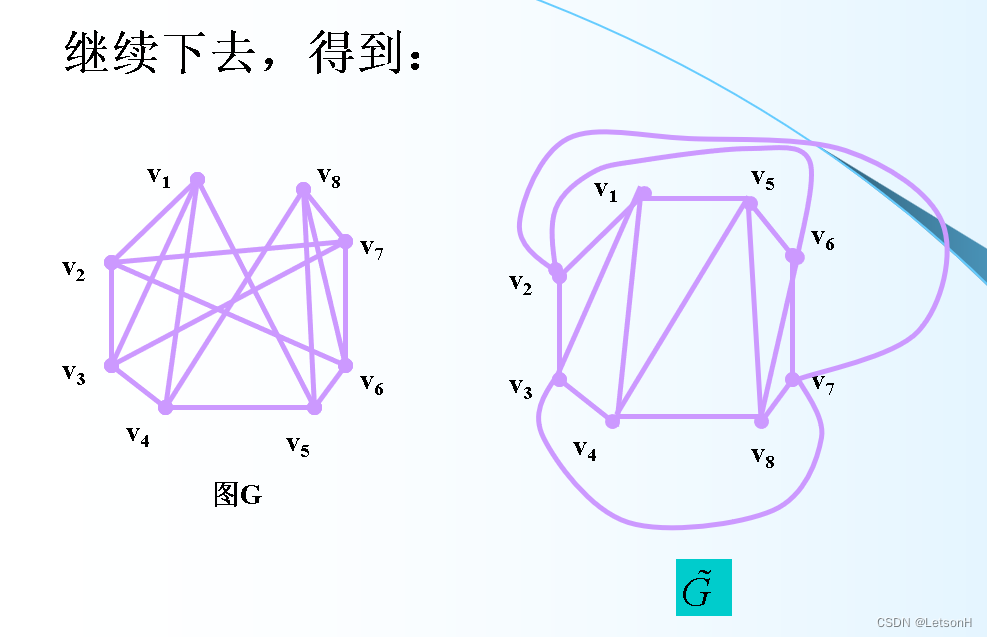
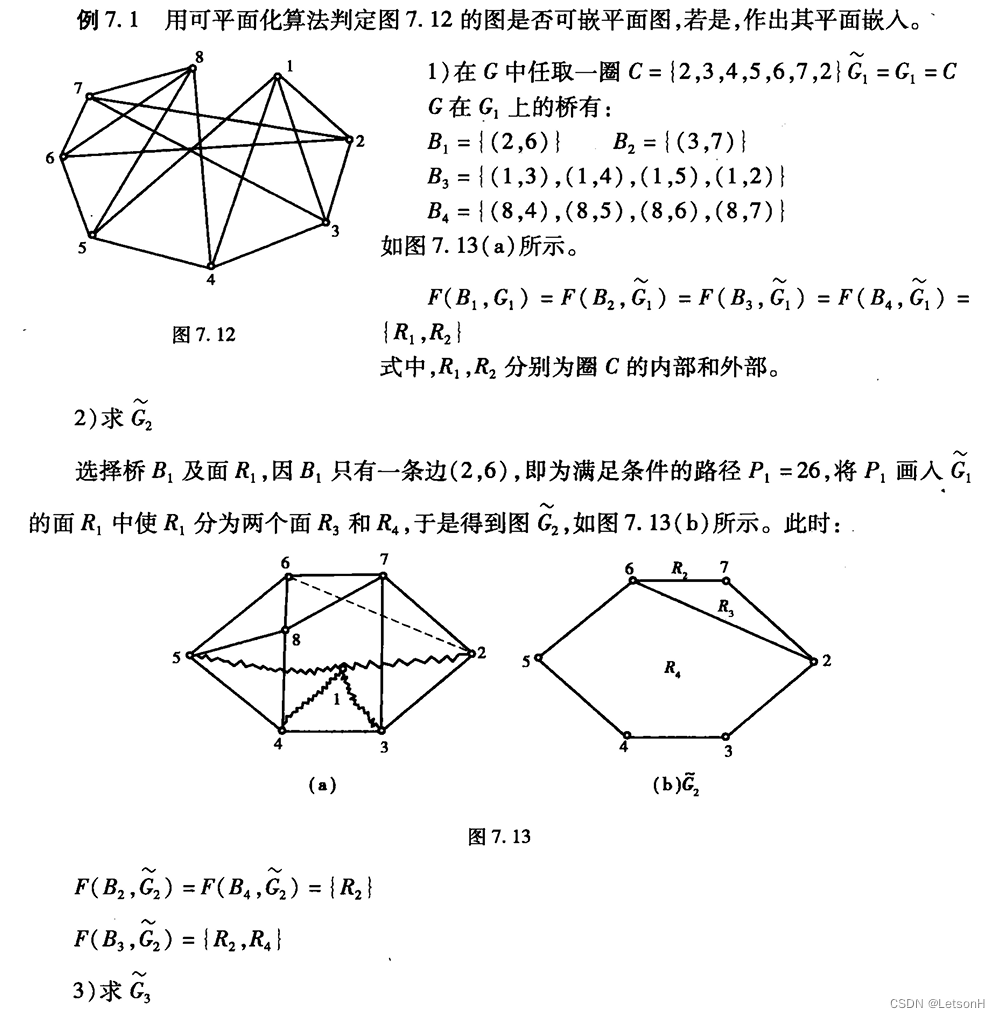
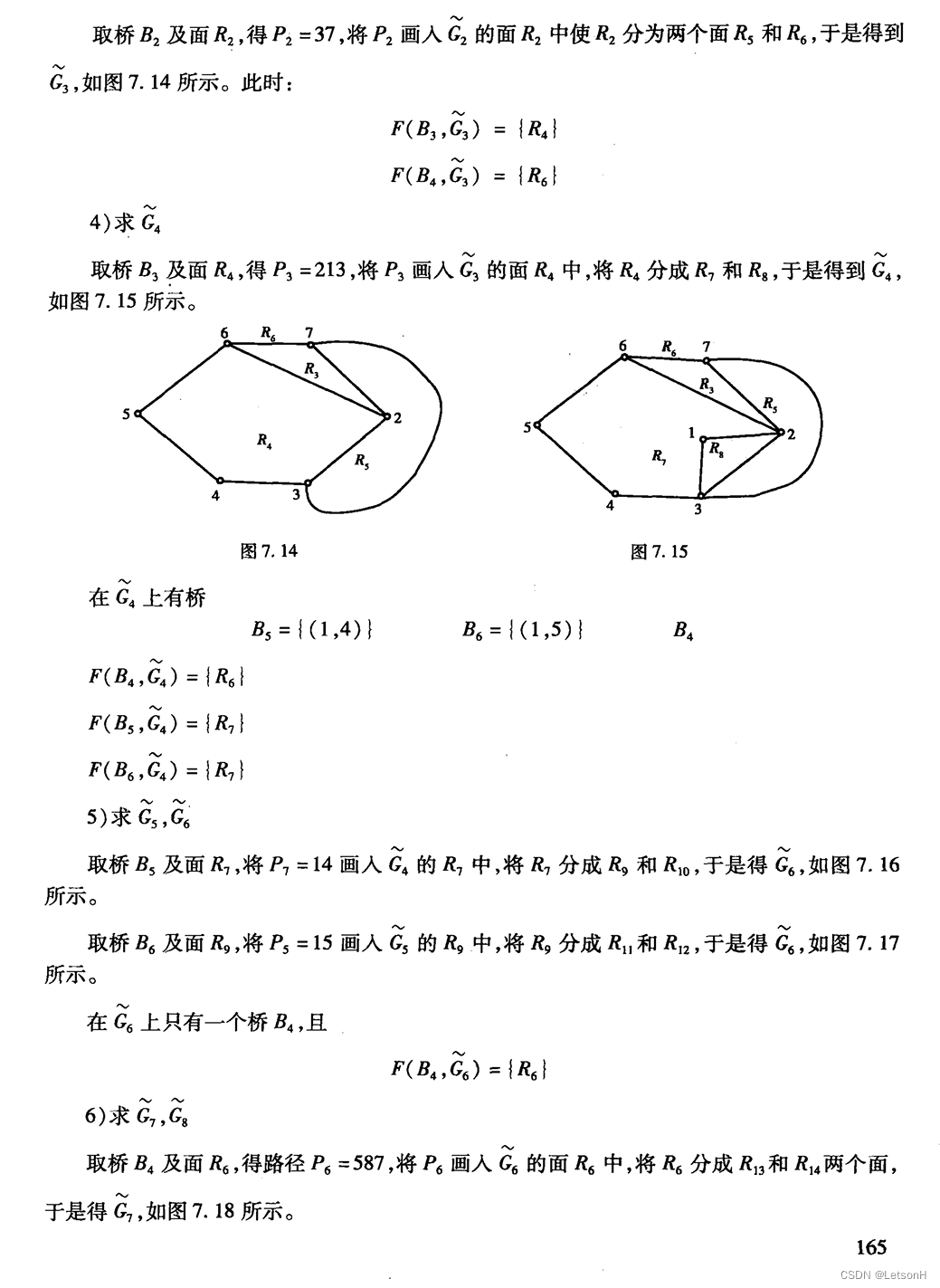
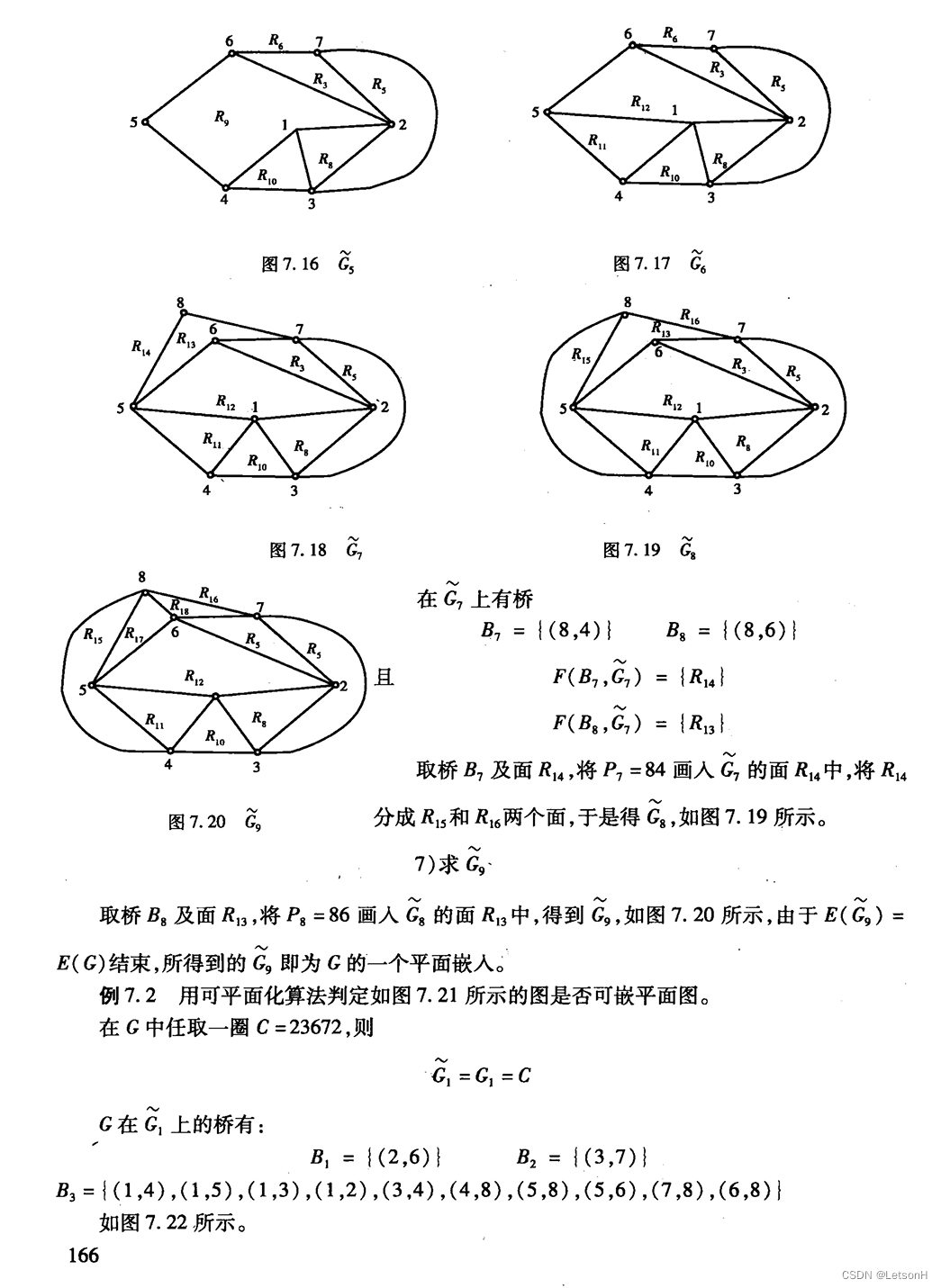
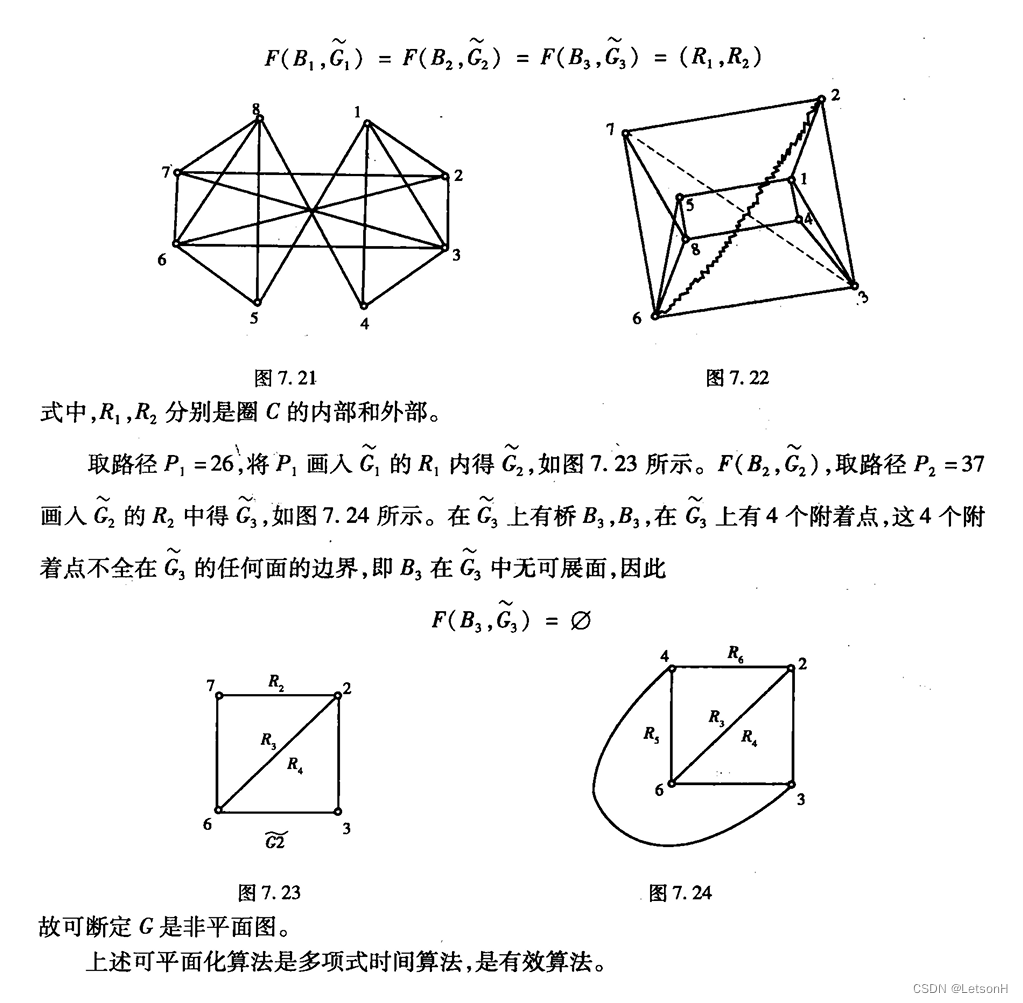
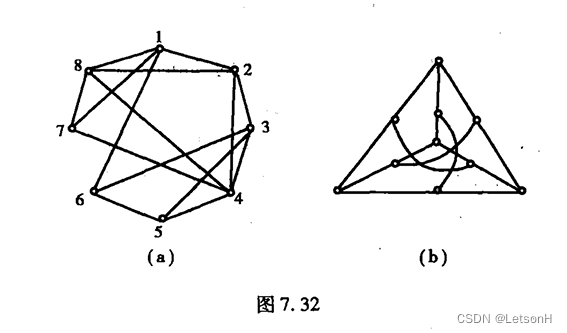
第七章:7.1、7.2、7.3、7.4、7.5
填空
计算
作业
历年真题1
历年真题2
历年真题3
声明:本站所有文章,如无特殊说明或标注,均为本站原创发布。任何个人或组织,在未征得本站同意时,禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益,可联系我们进行处理。


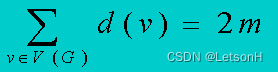
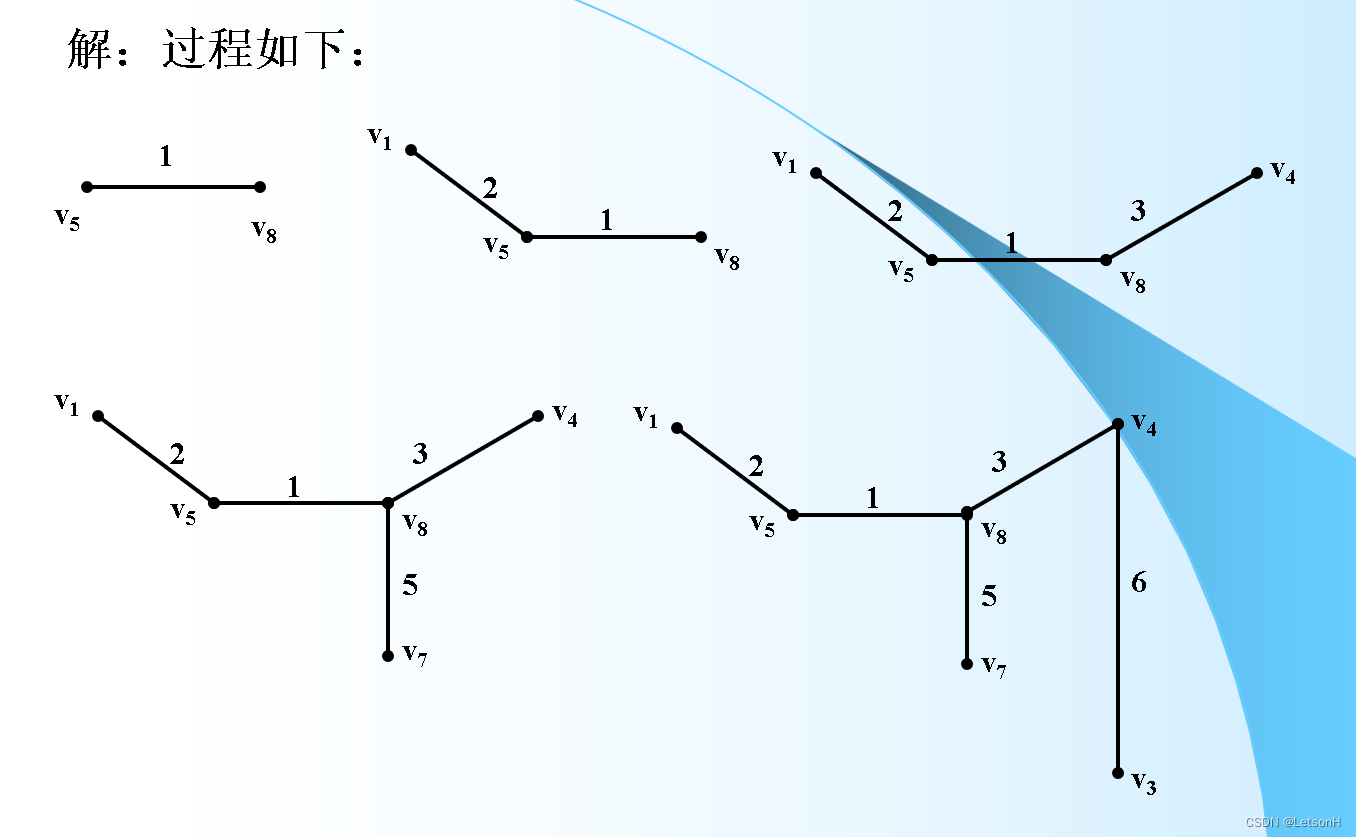
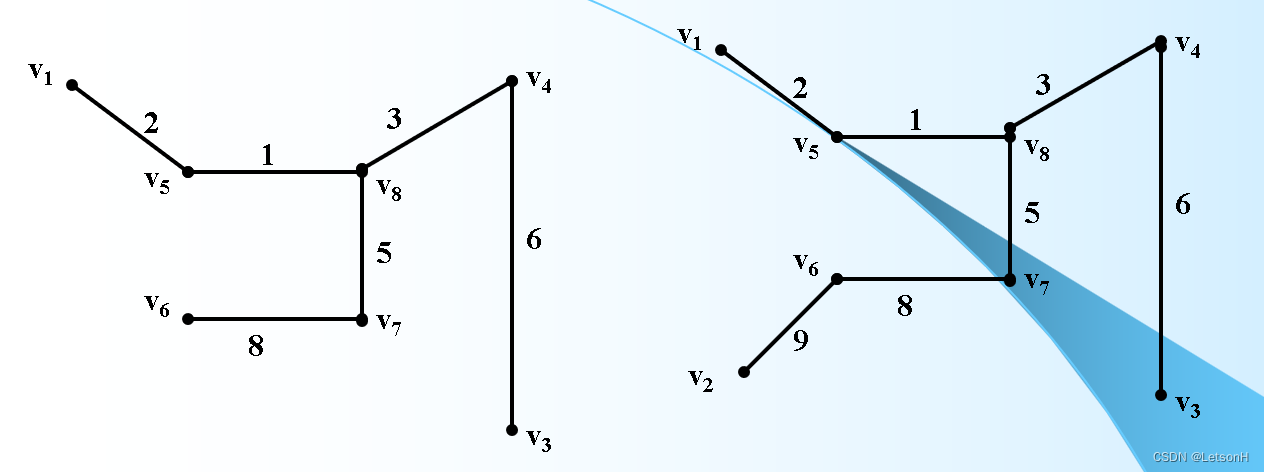
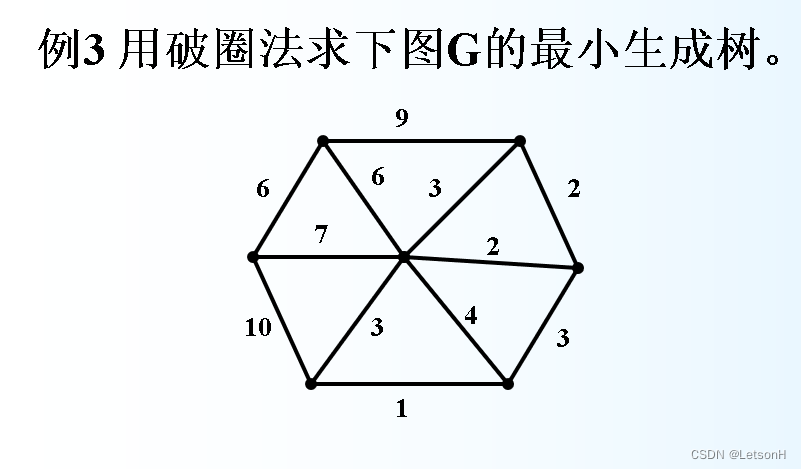

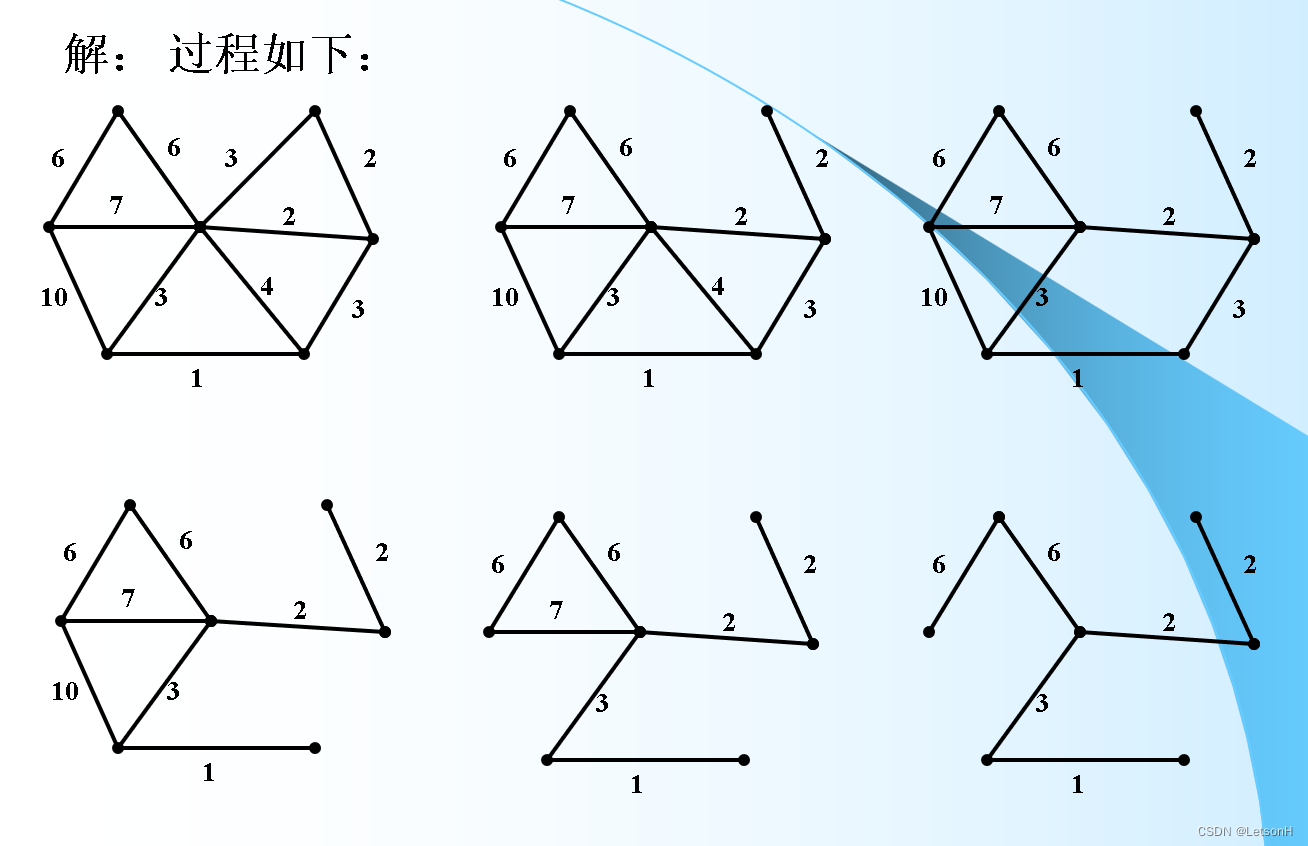
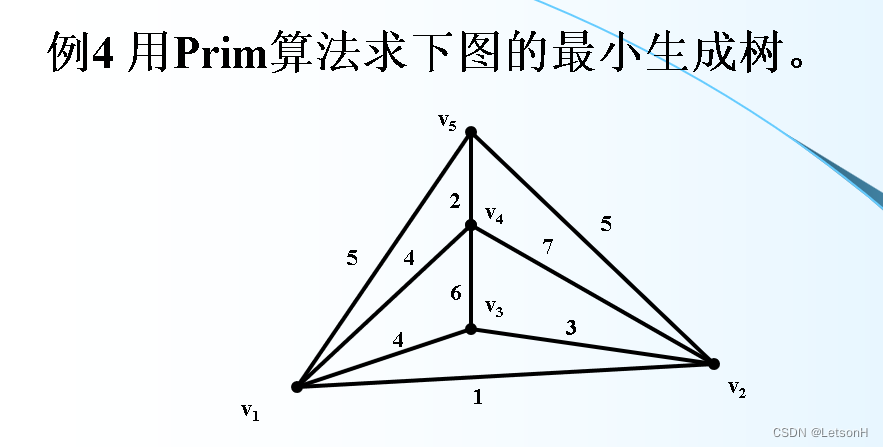

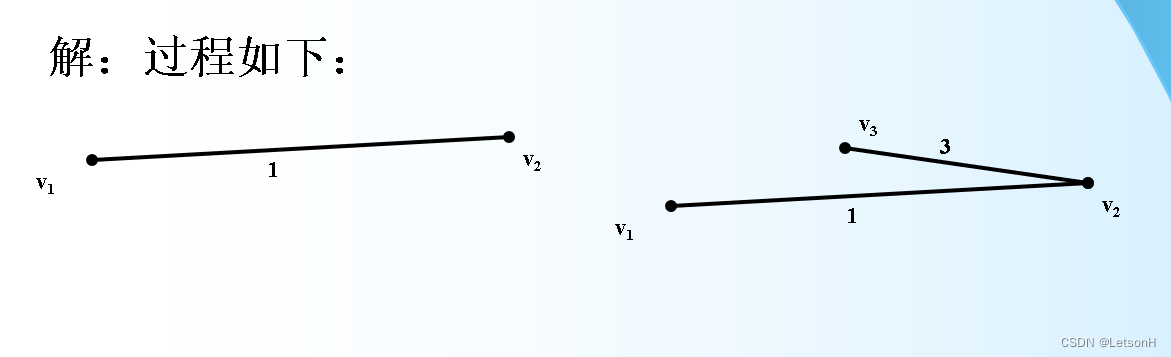
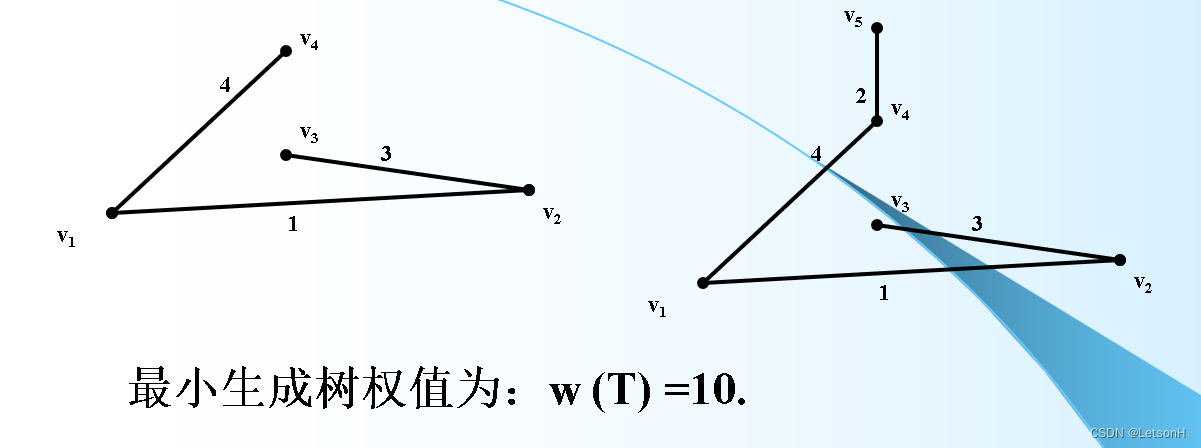


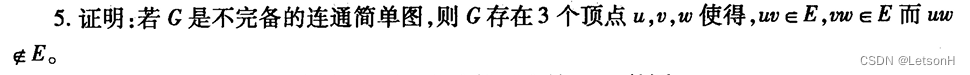

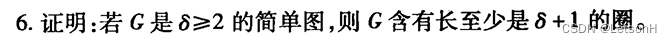

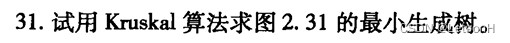
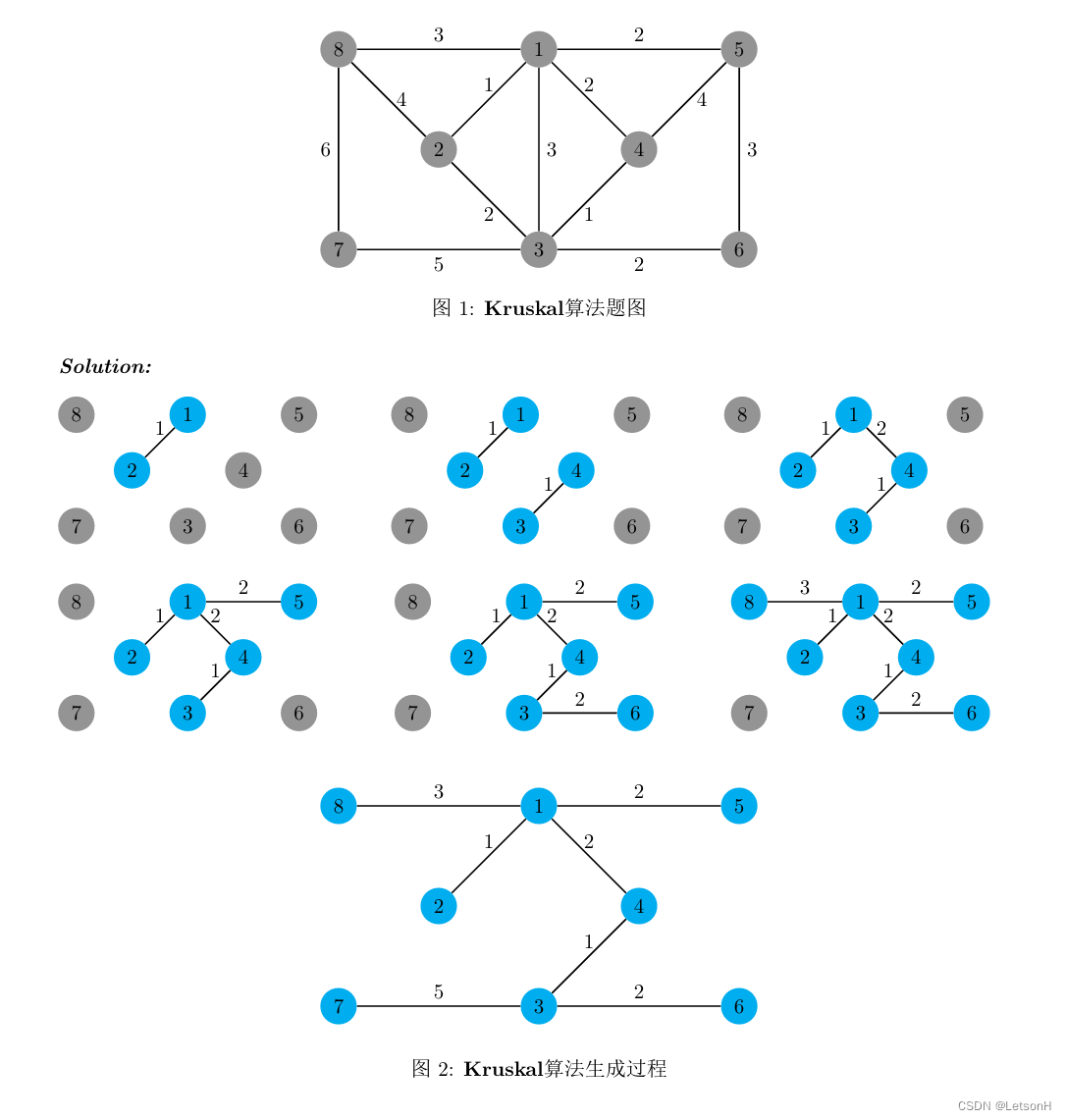
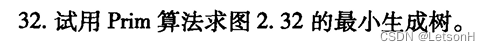
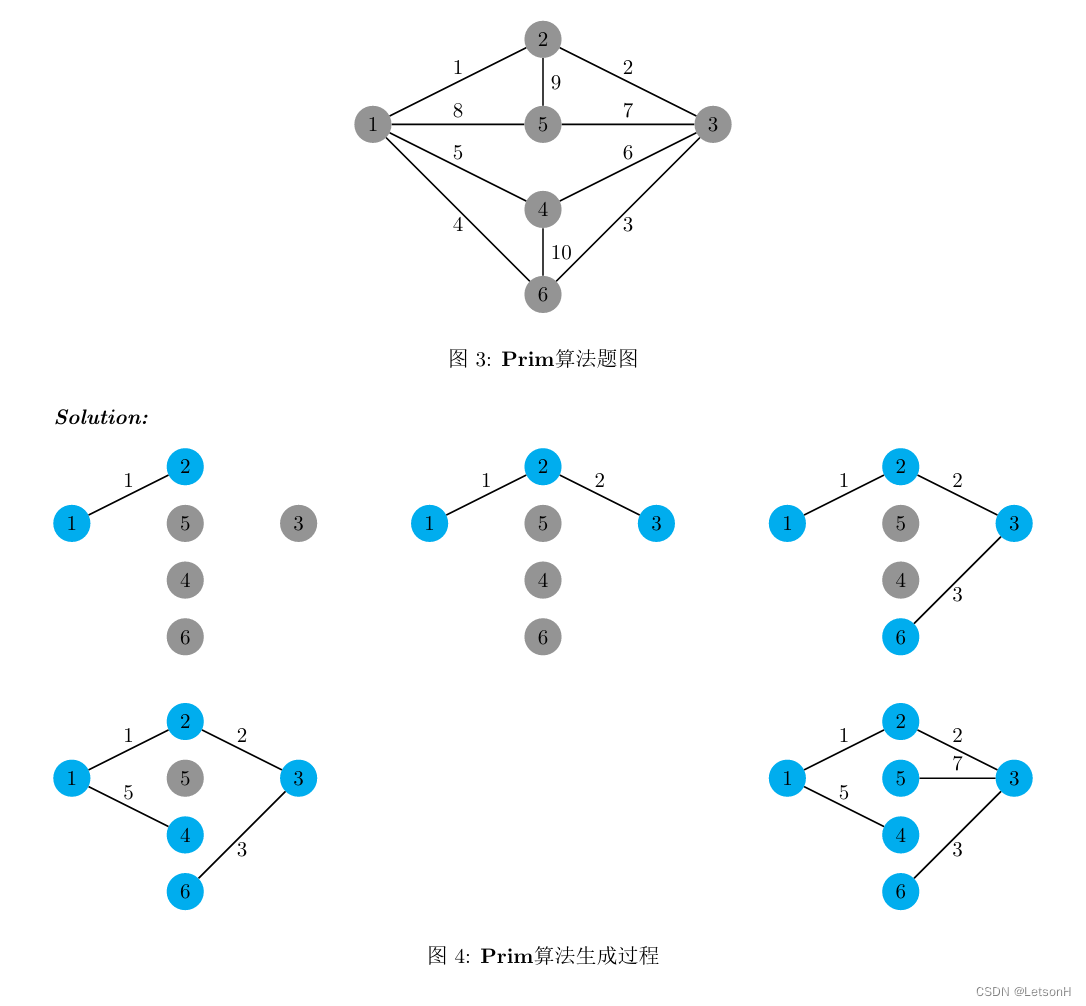
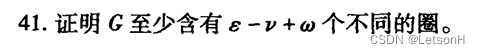

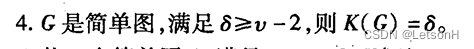

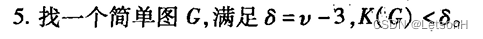
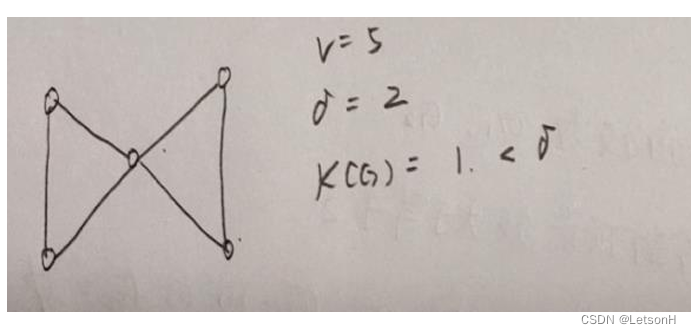


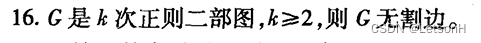



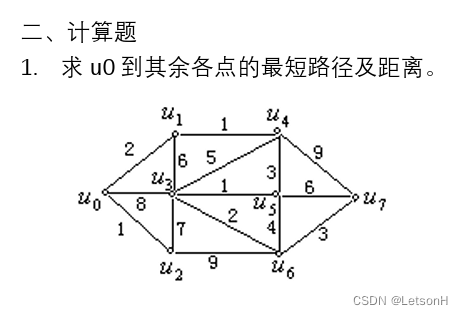
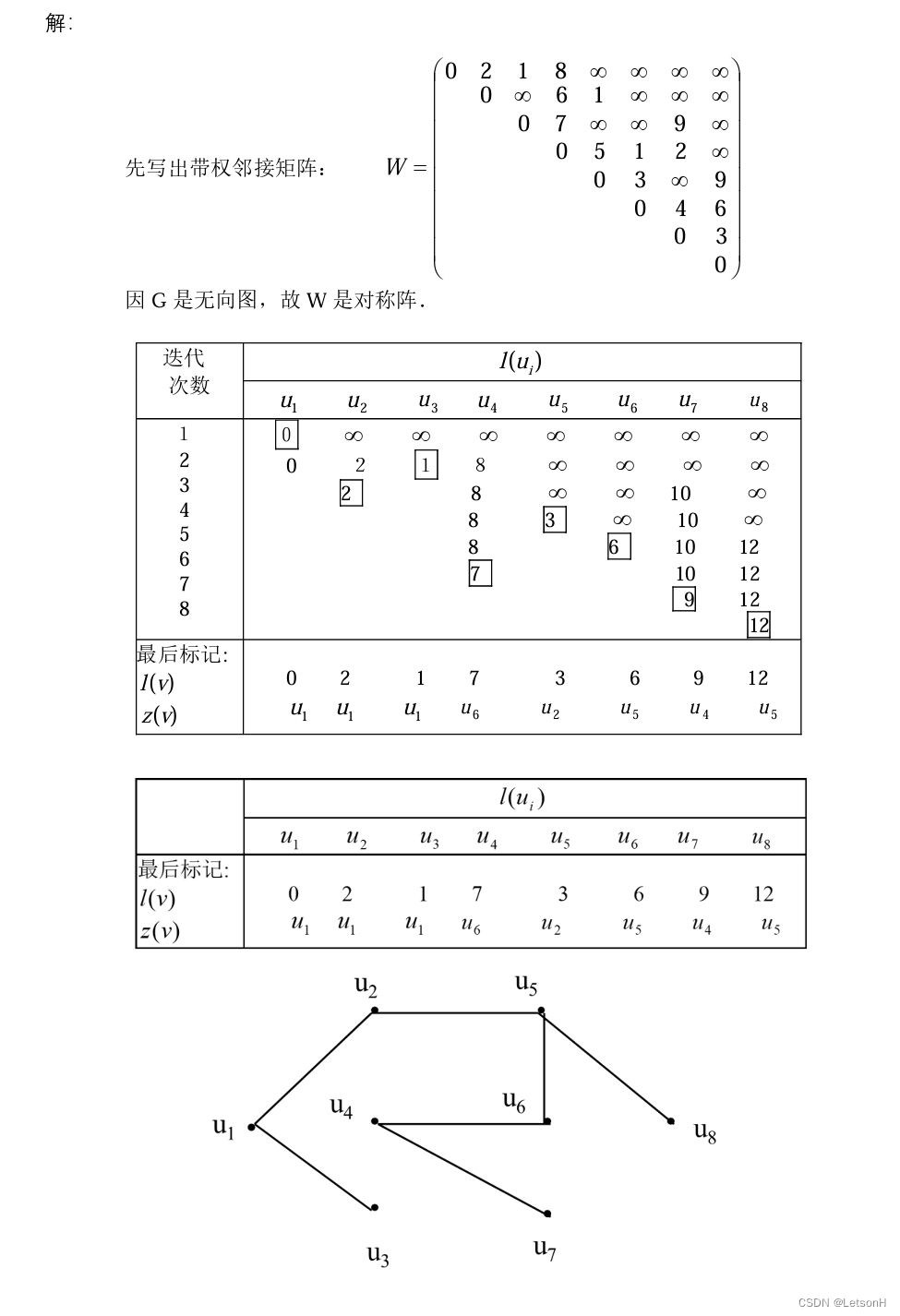
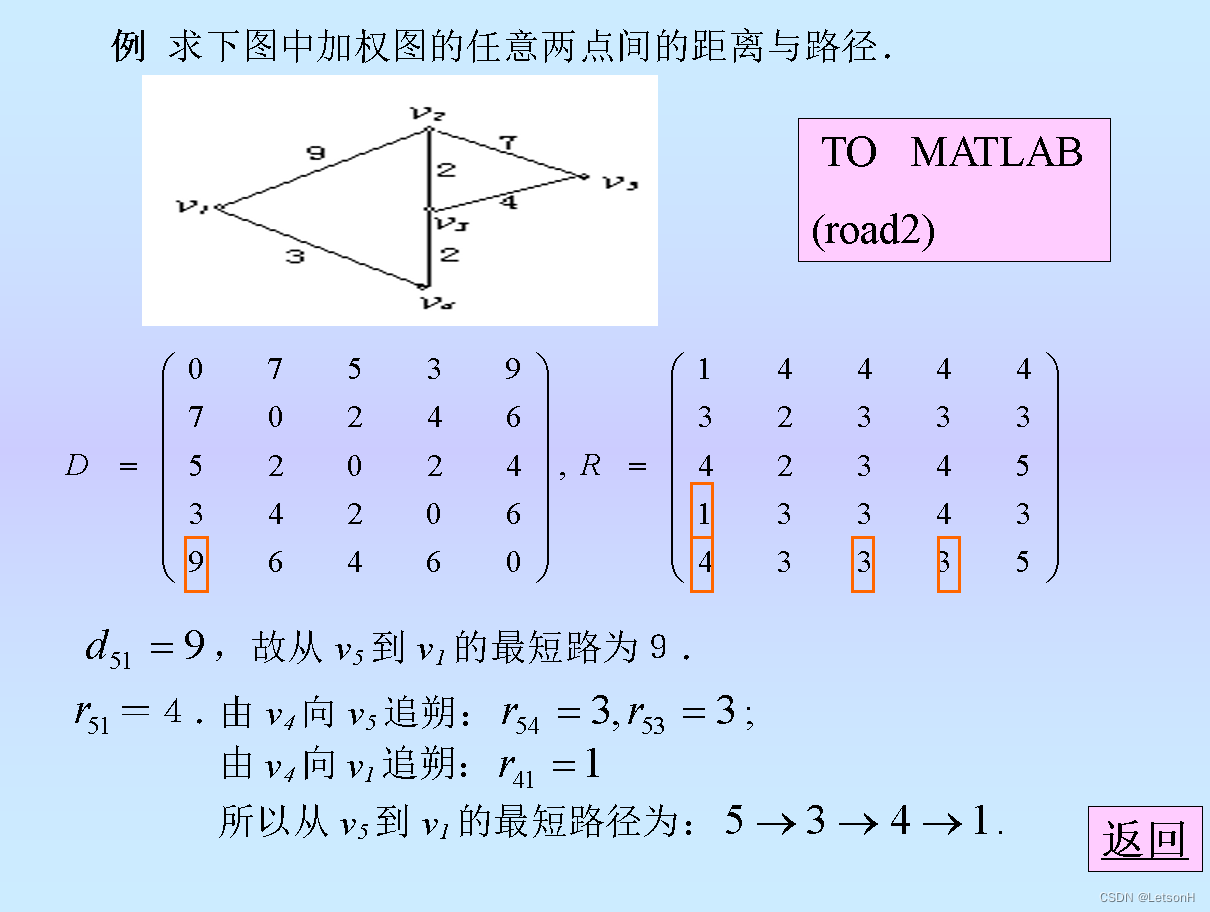
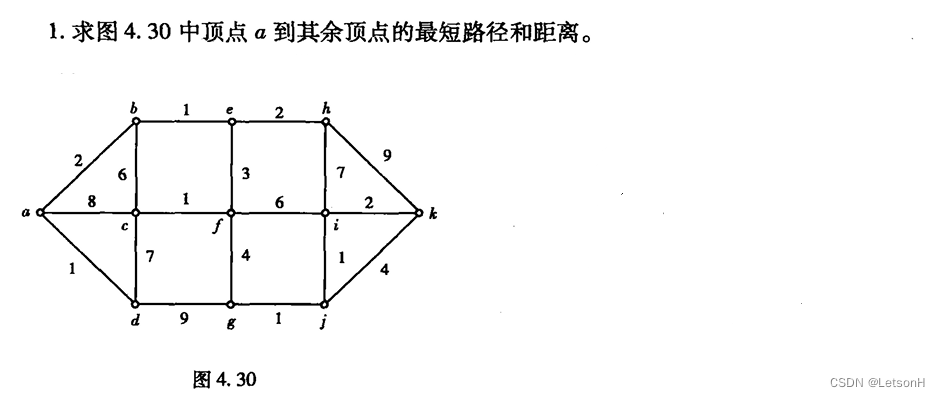
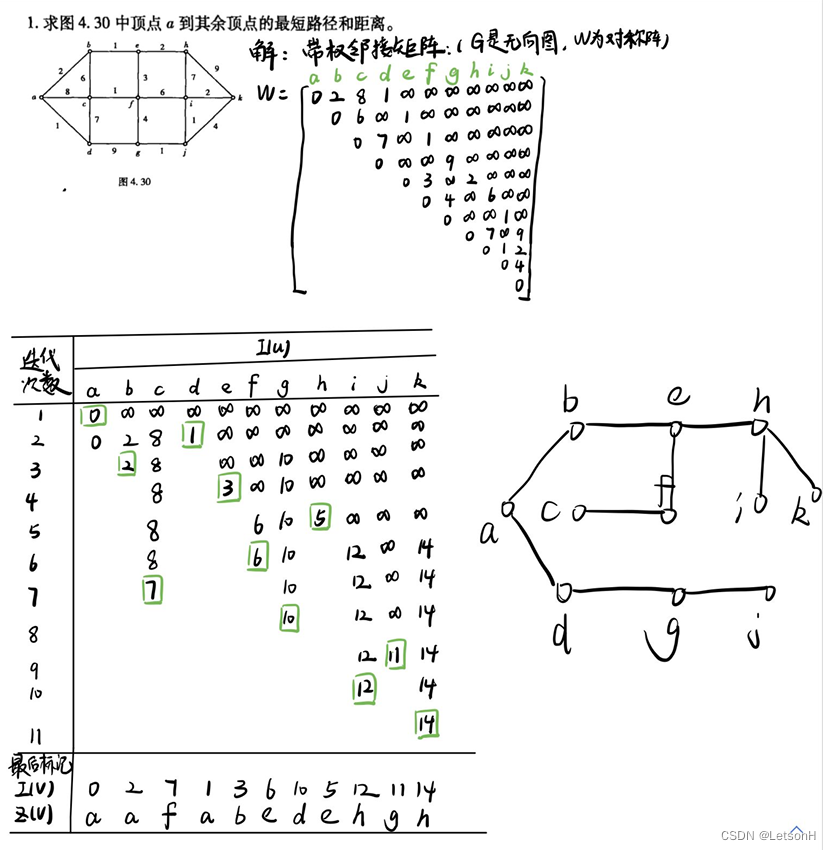


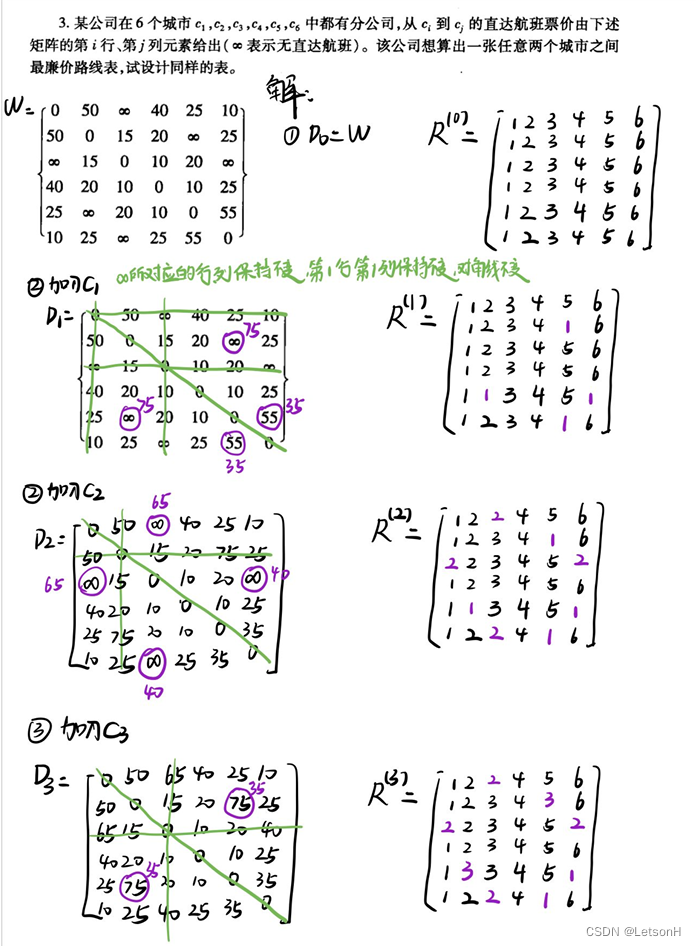
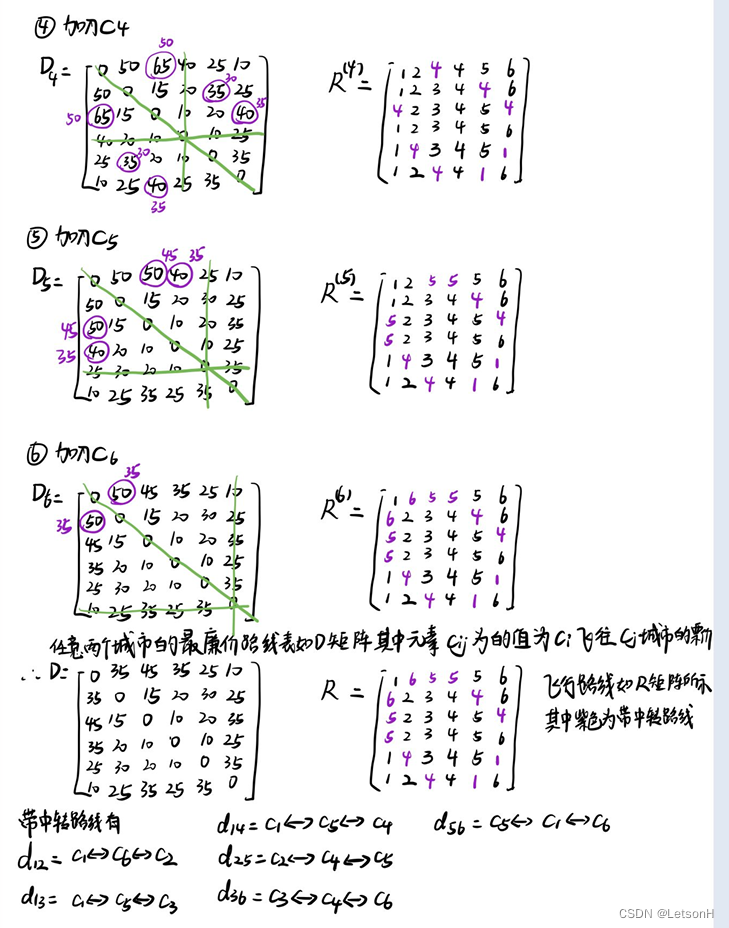
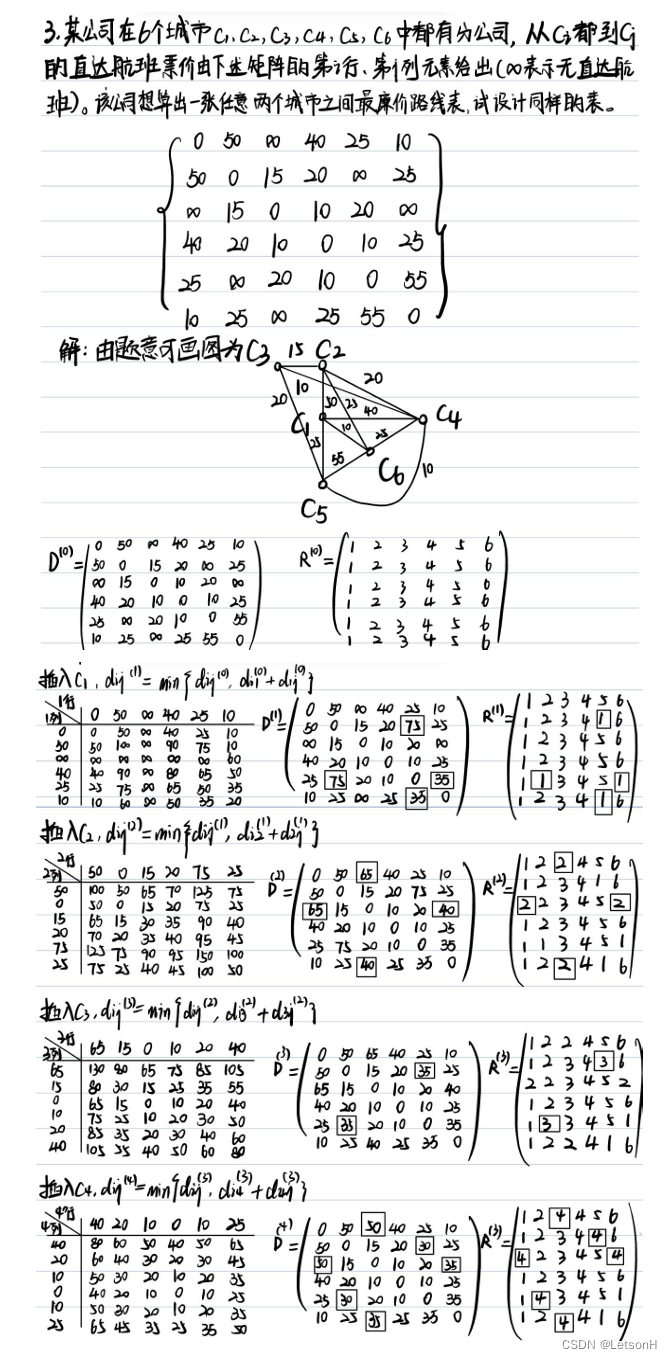

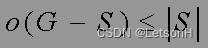
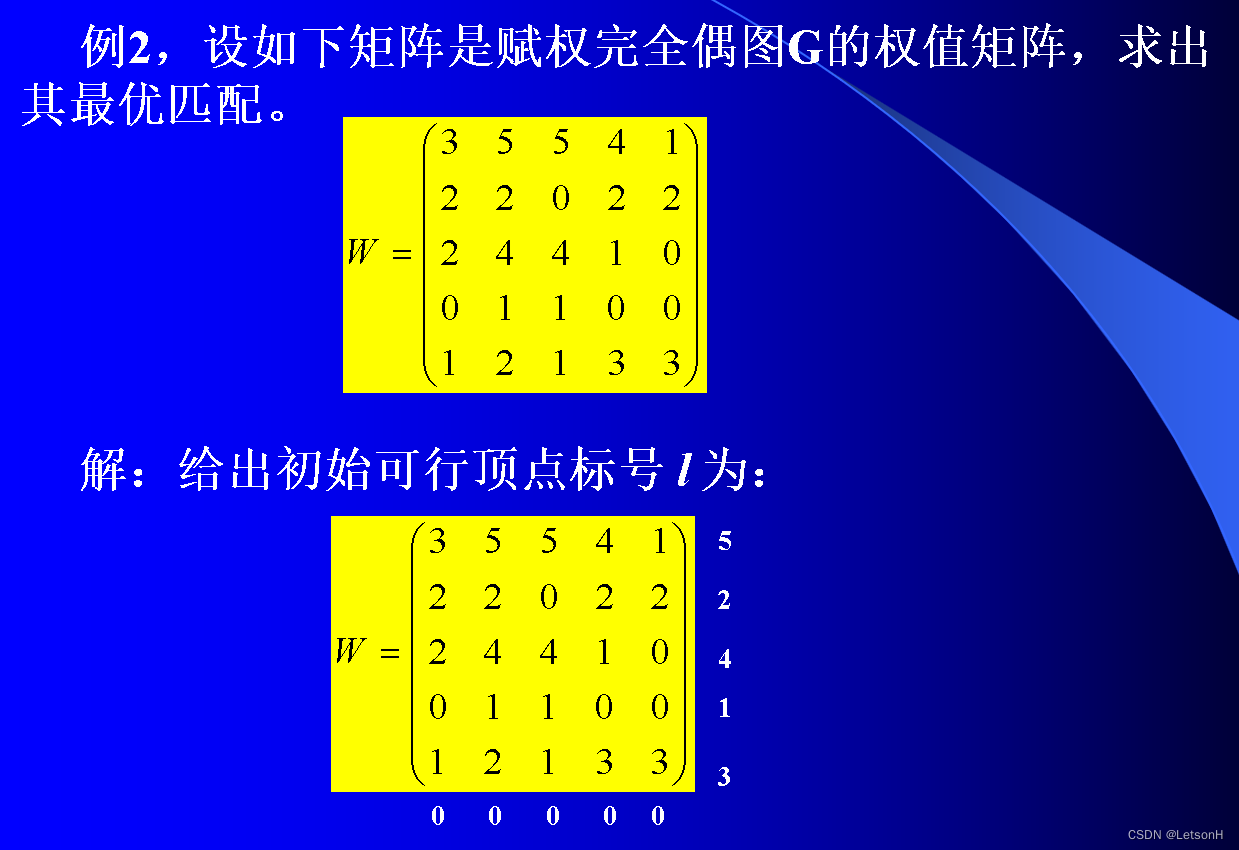
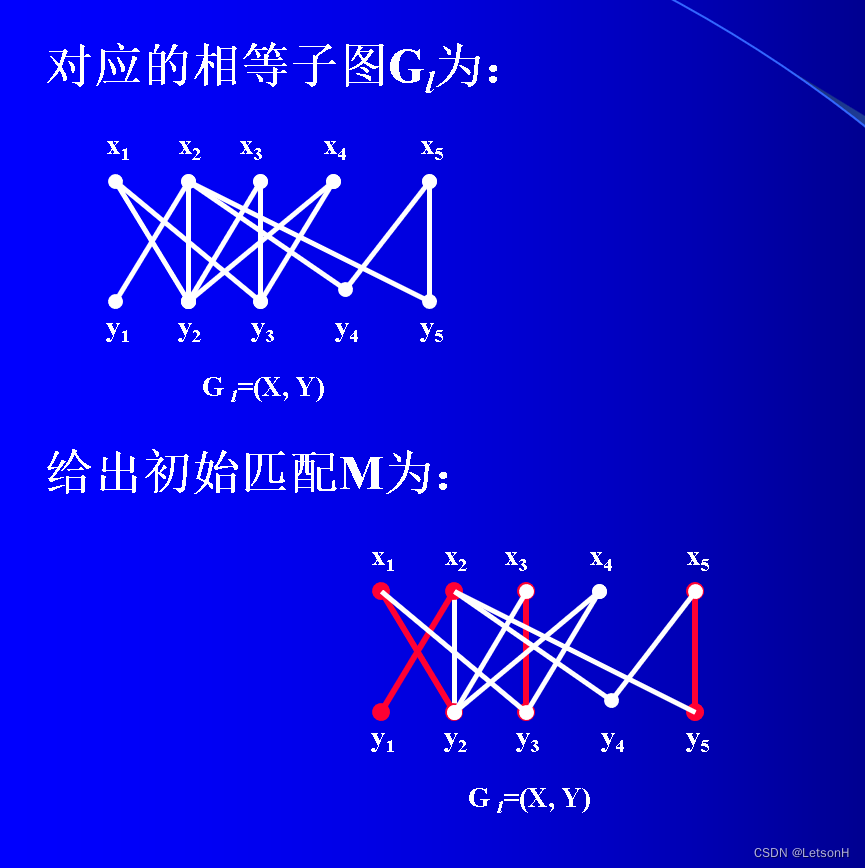

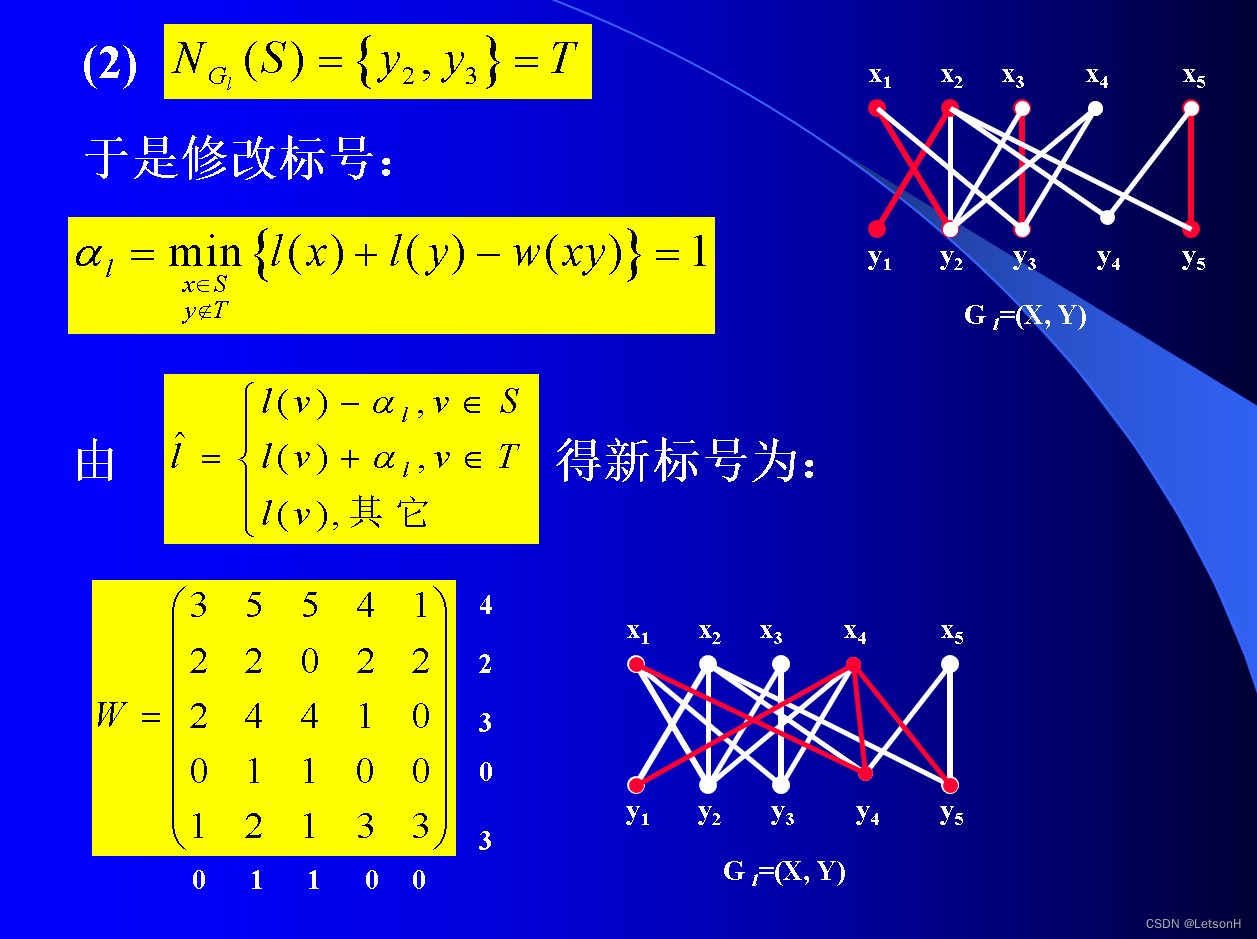

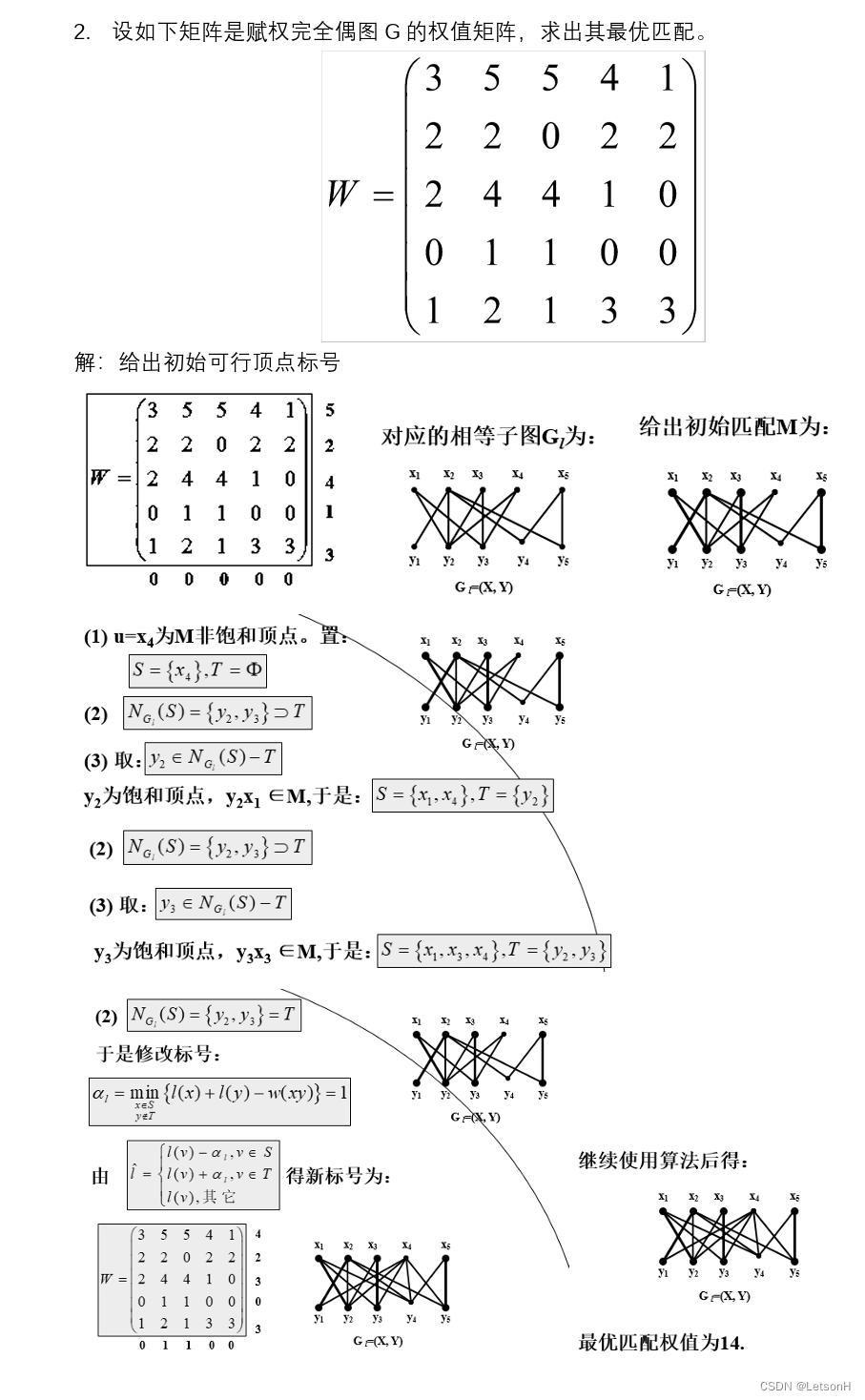

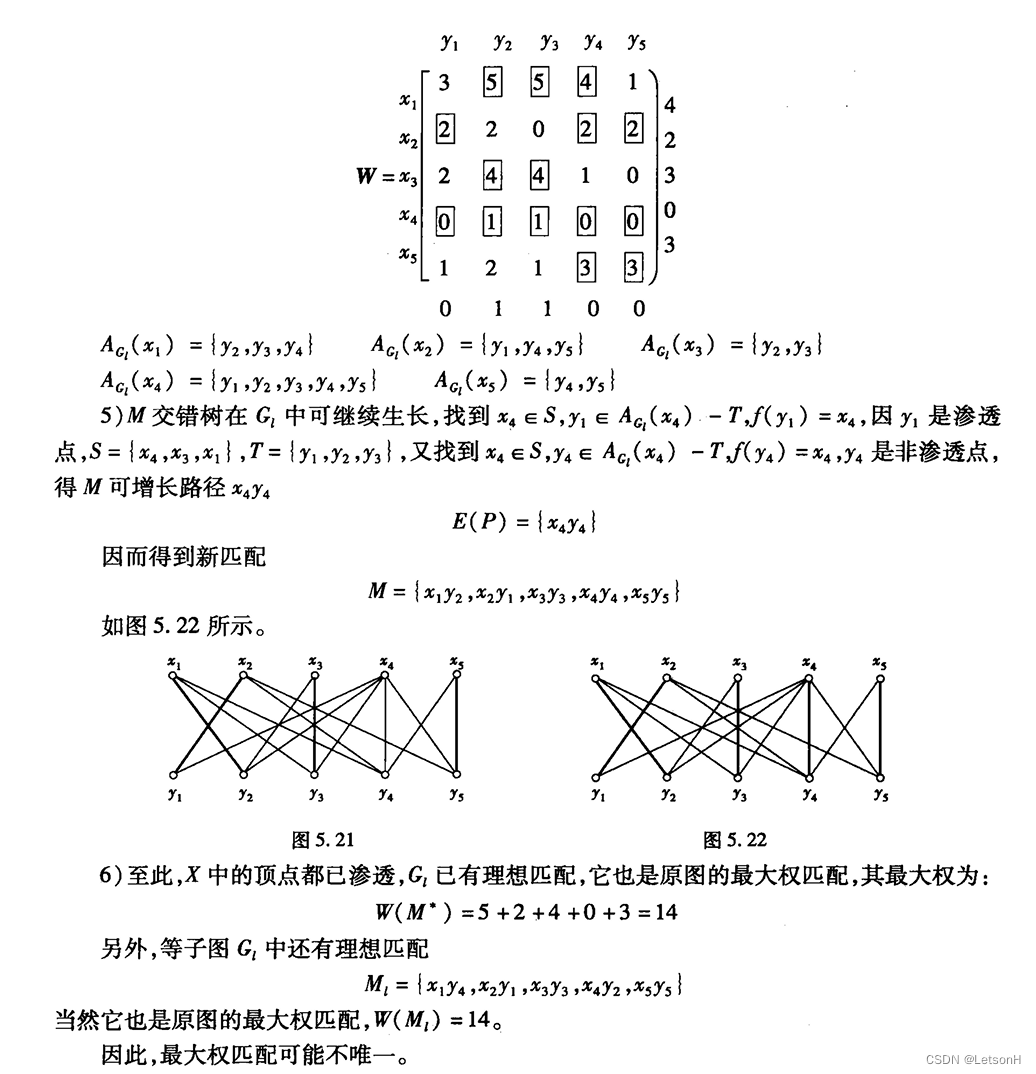
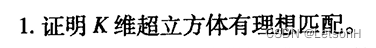



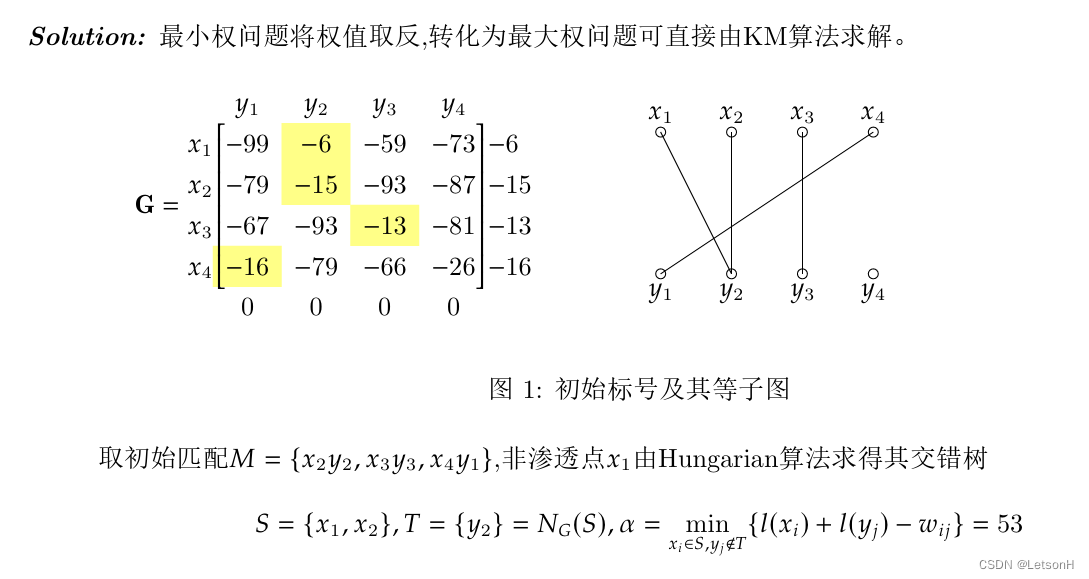








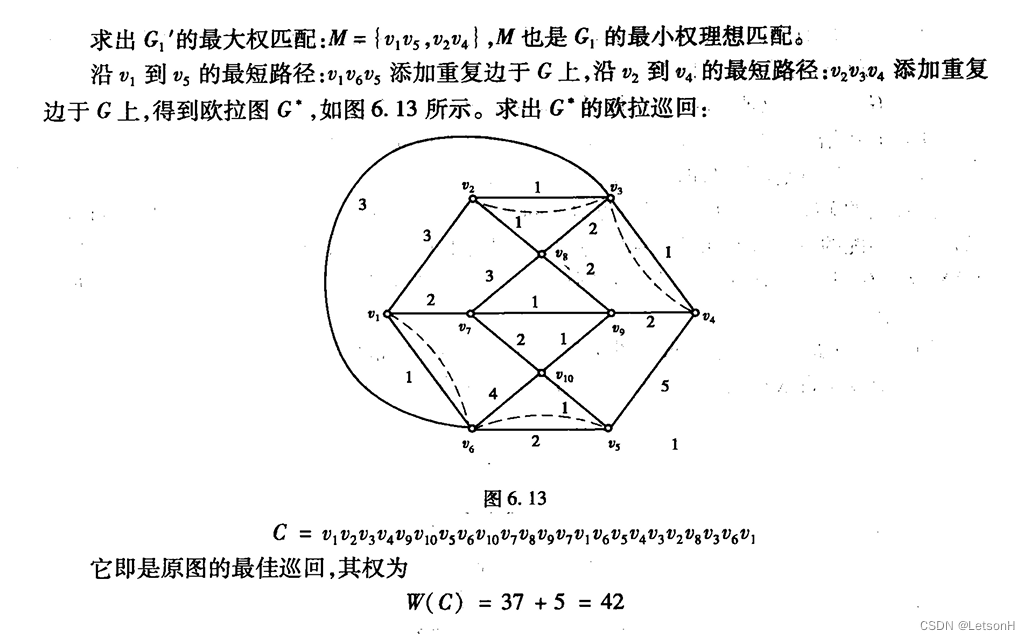
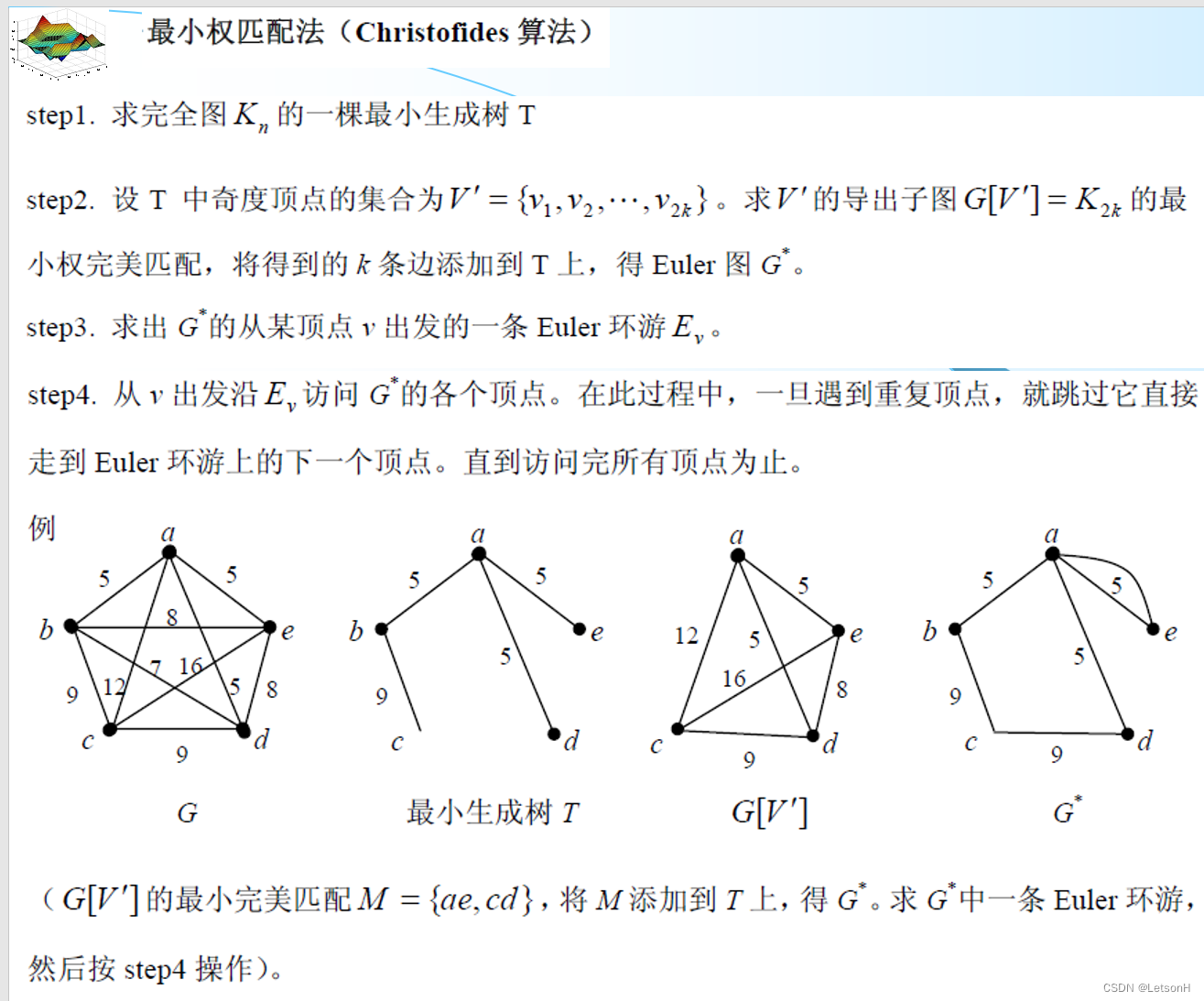
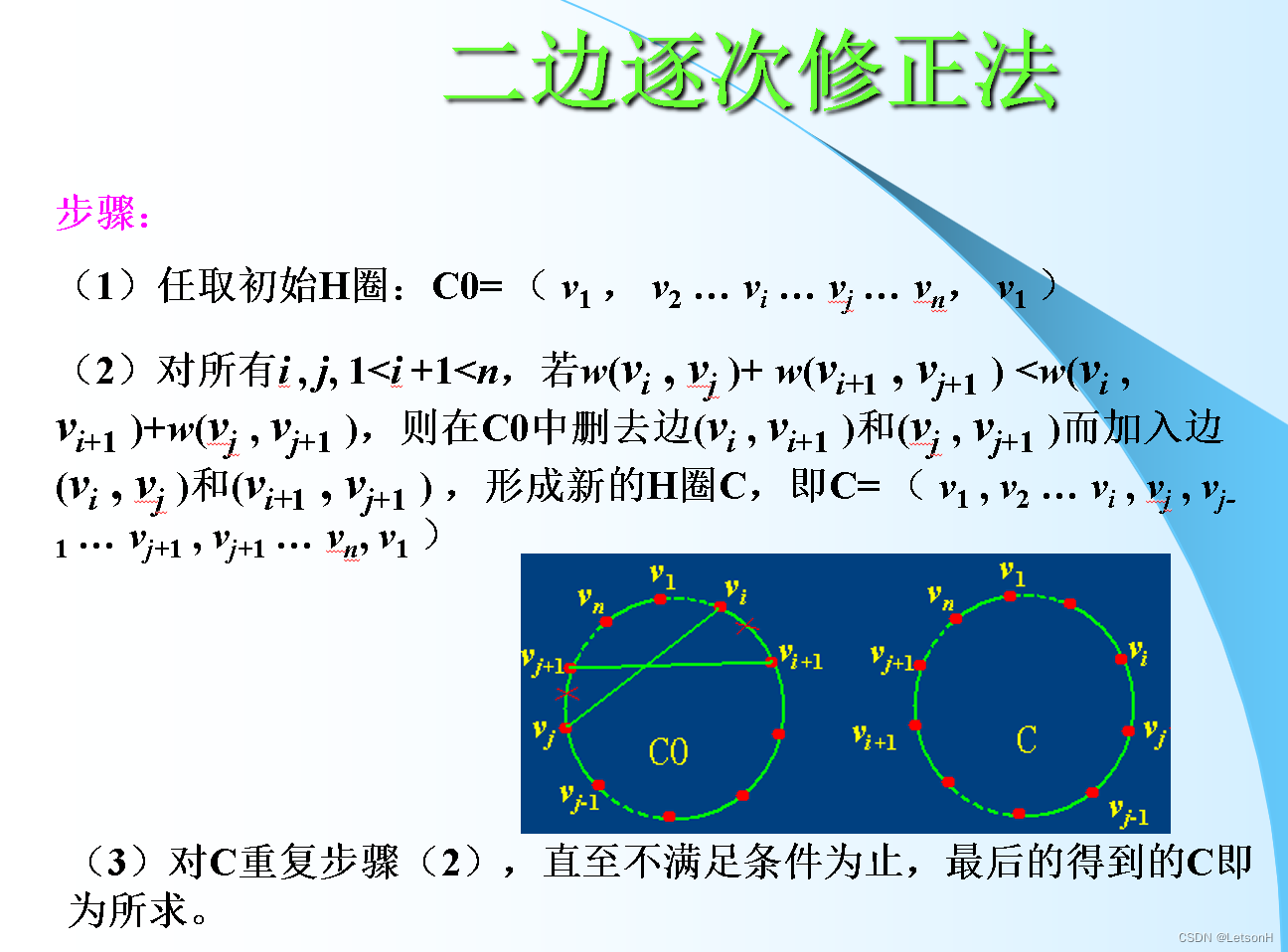
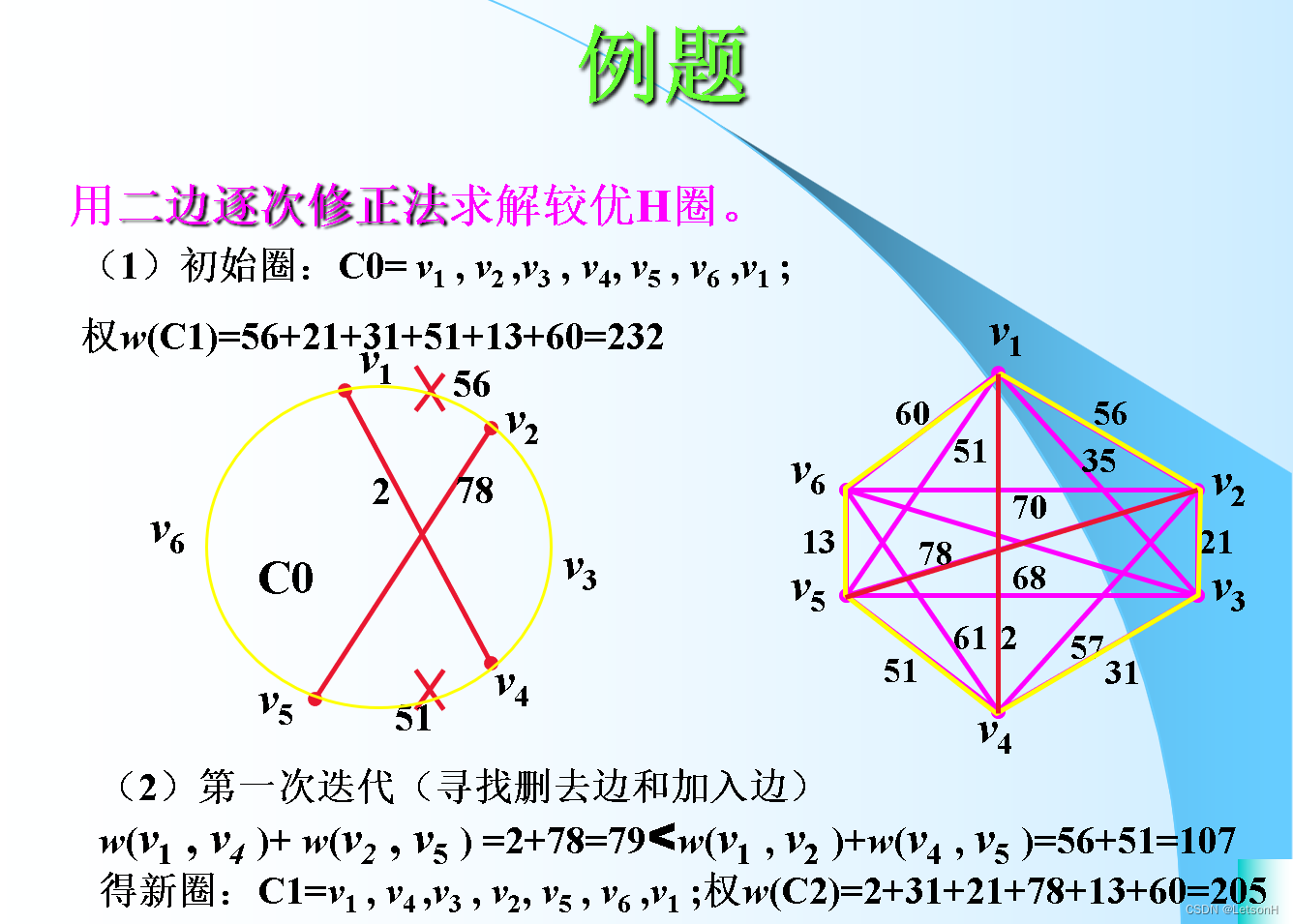
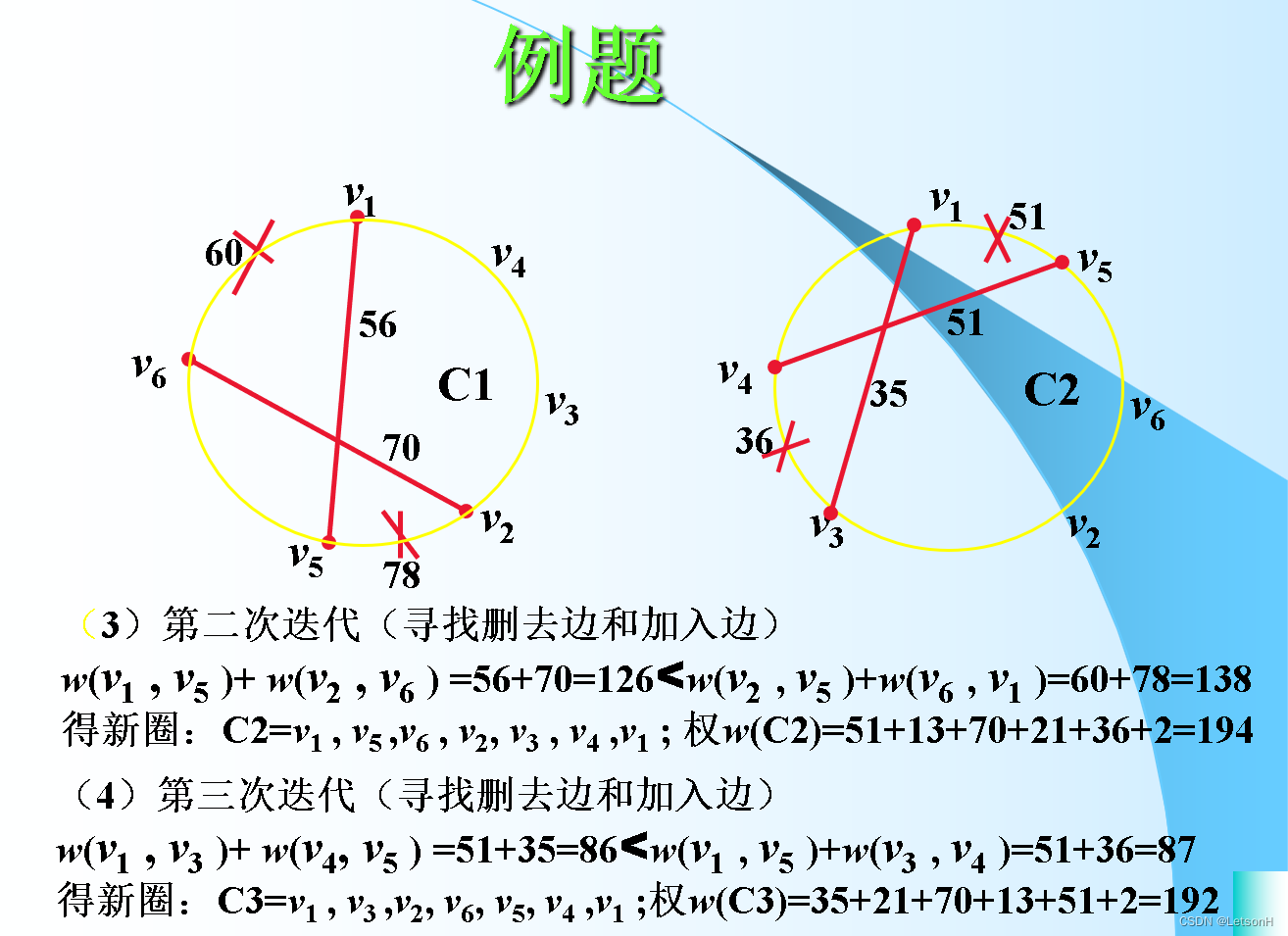
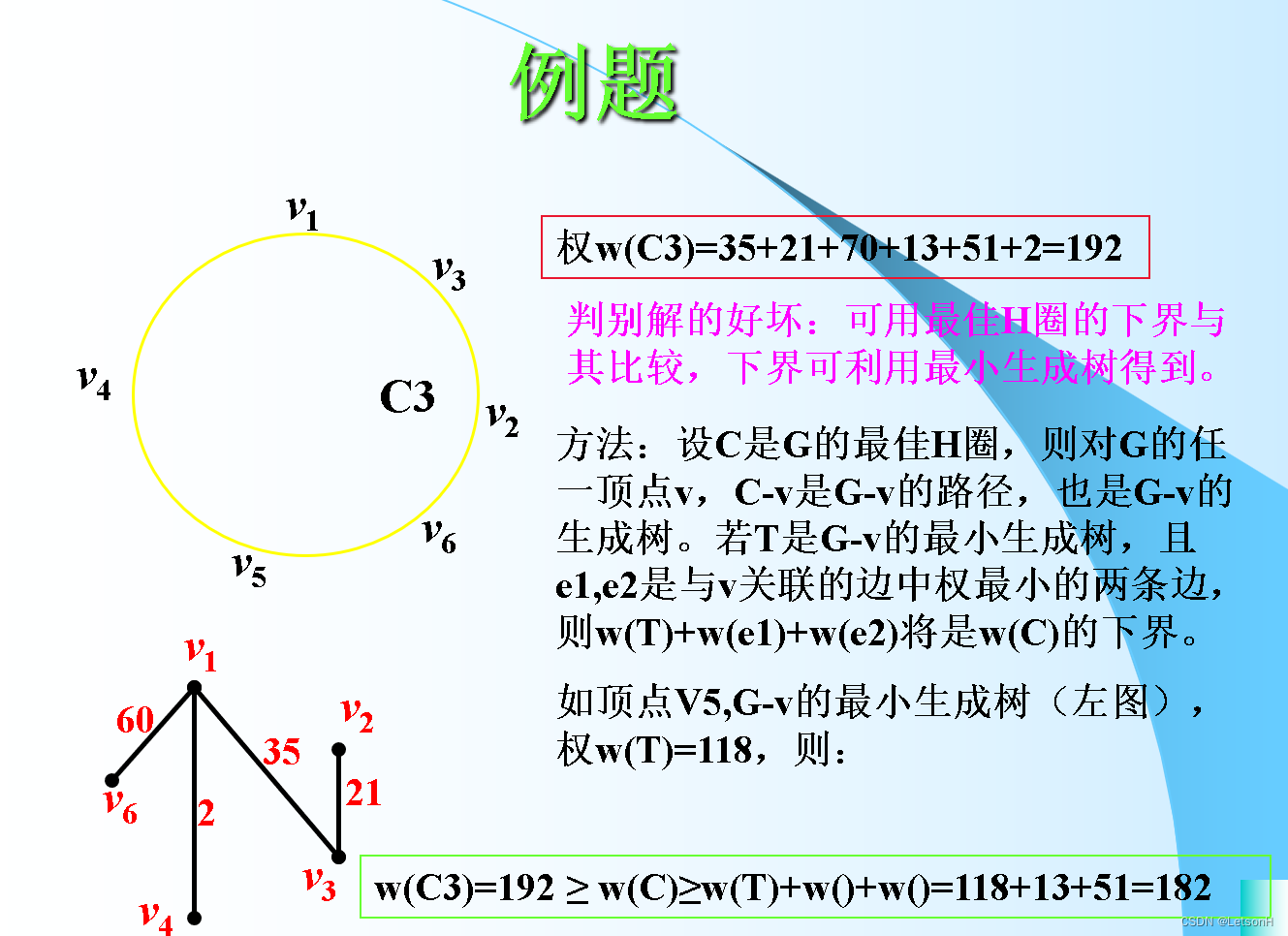

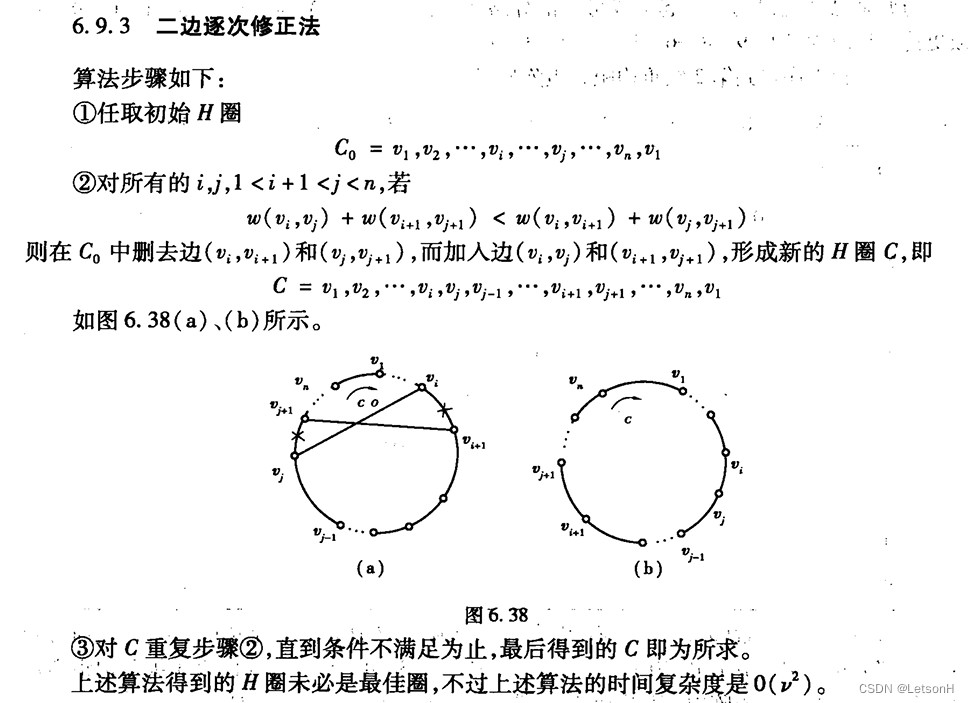
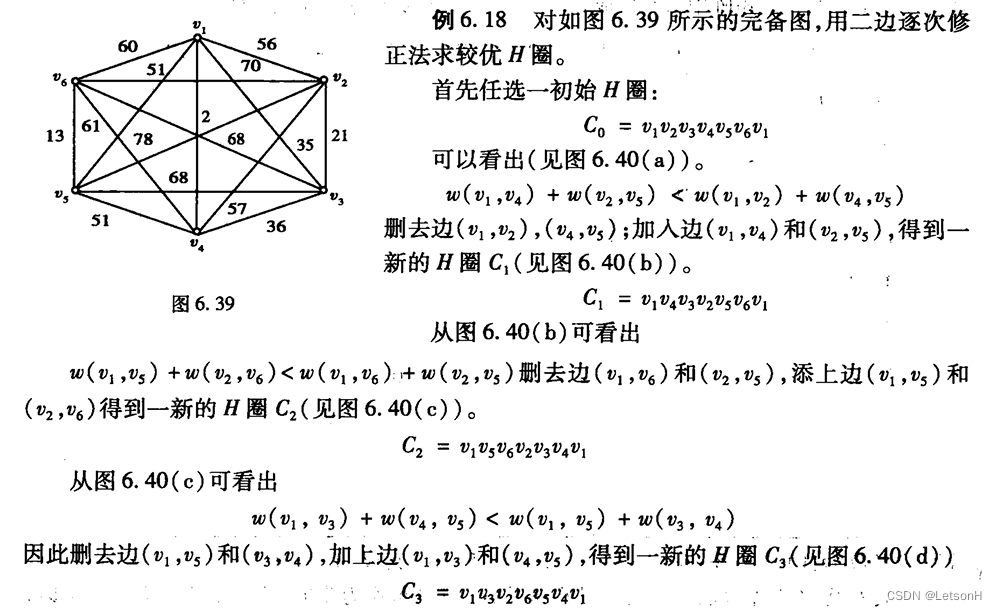
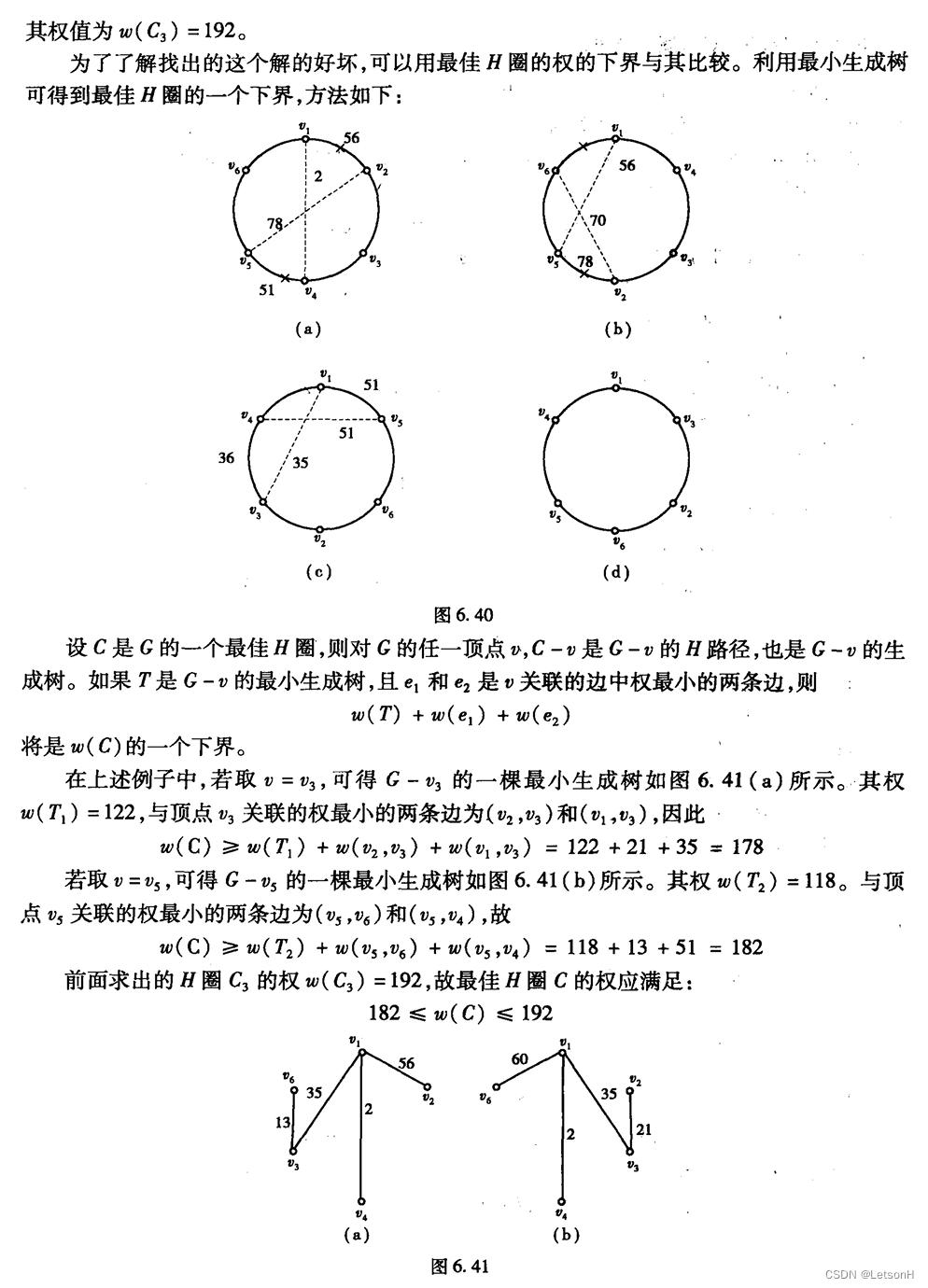
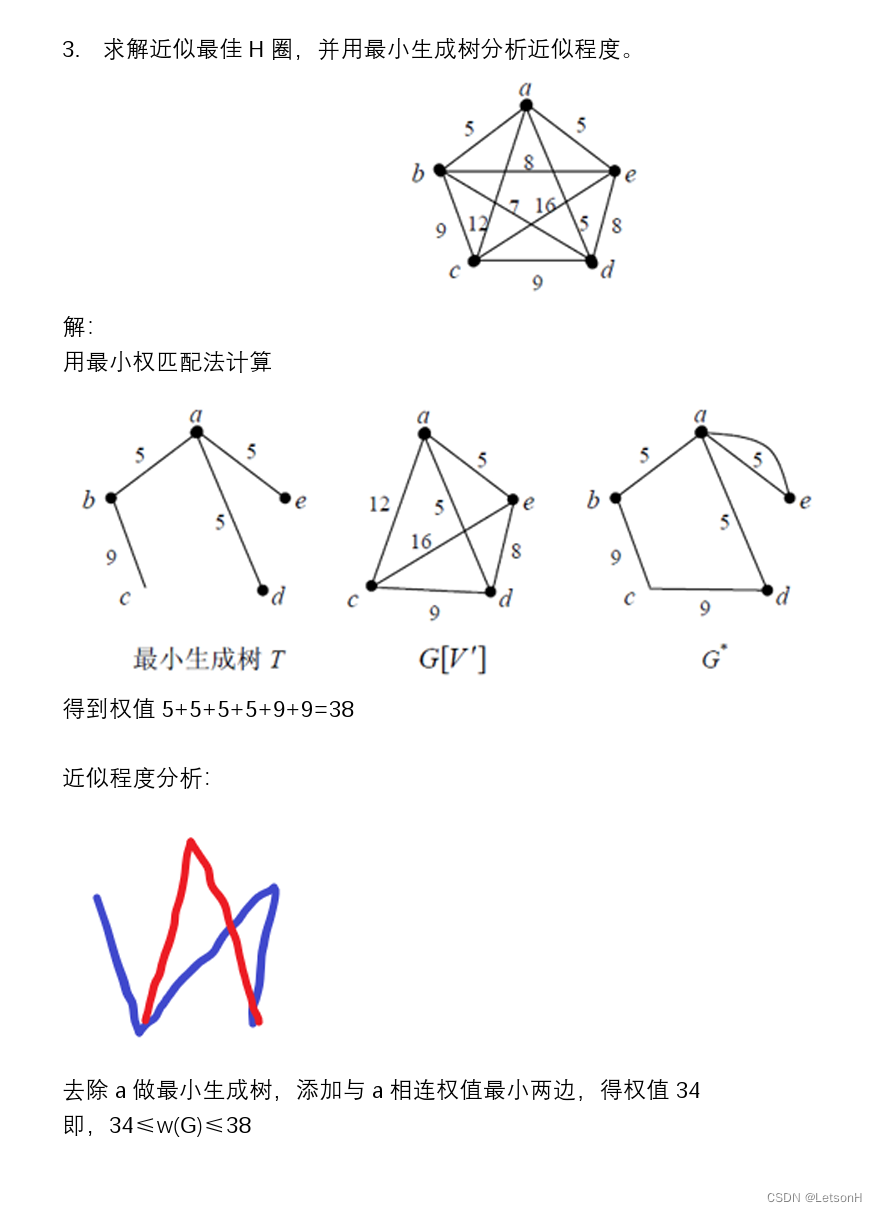


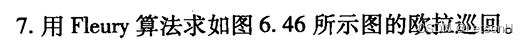
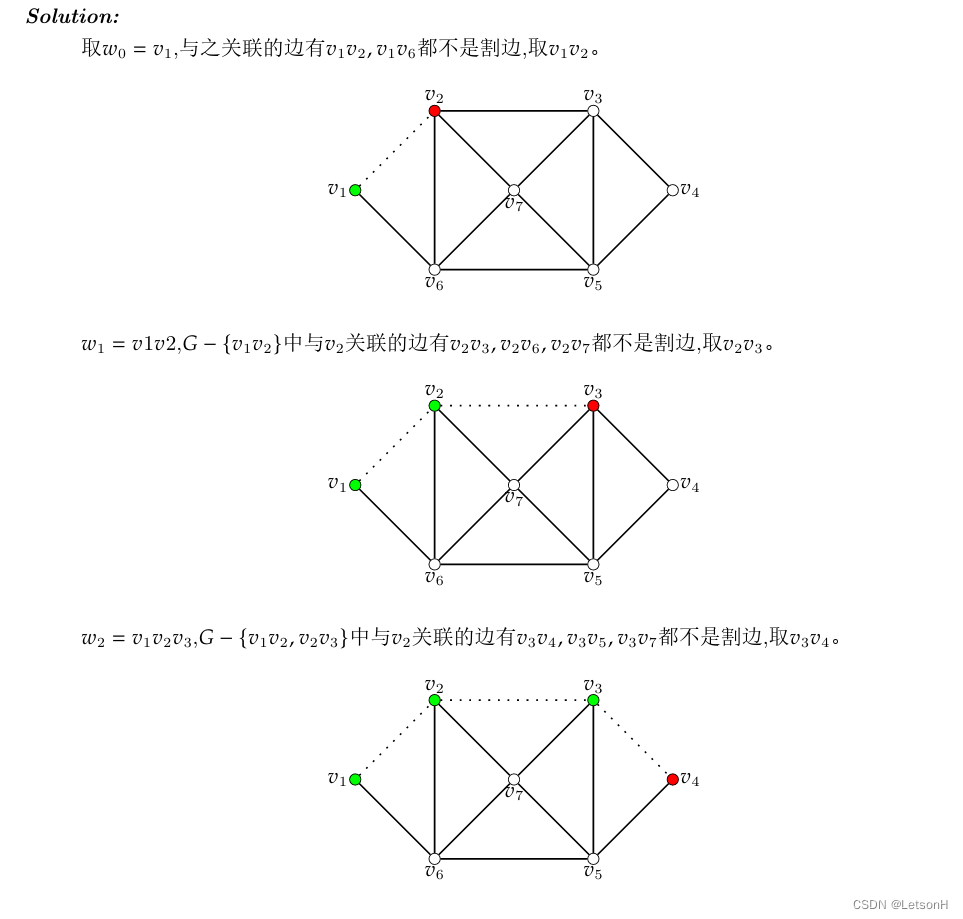
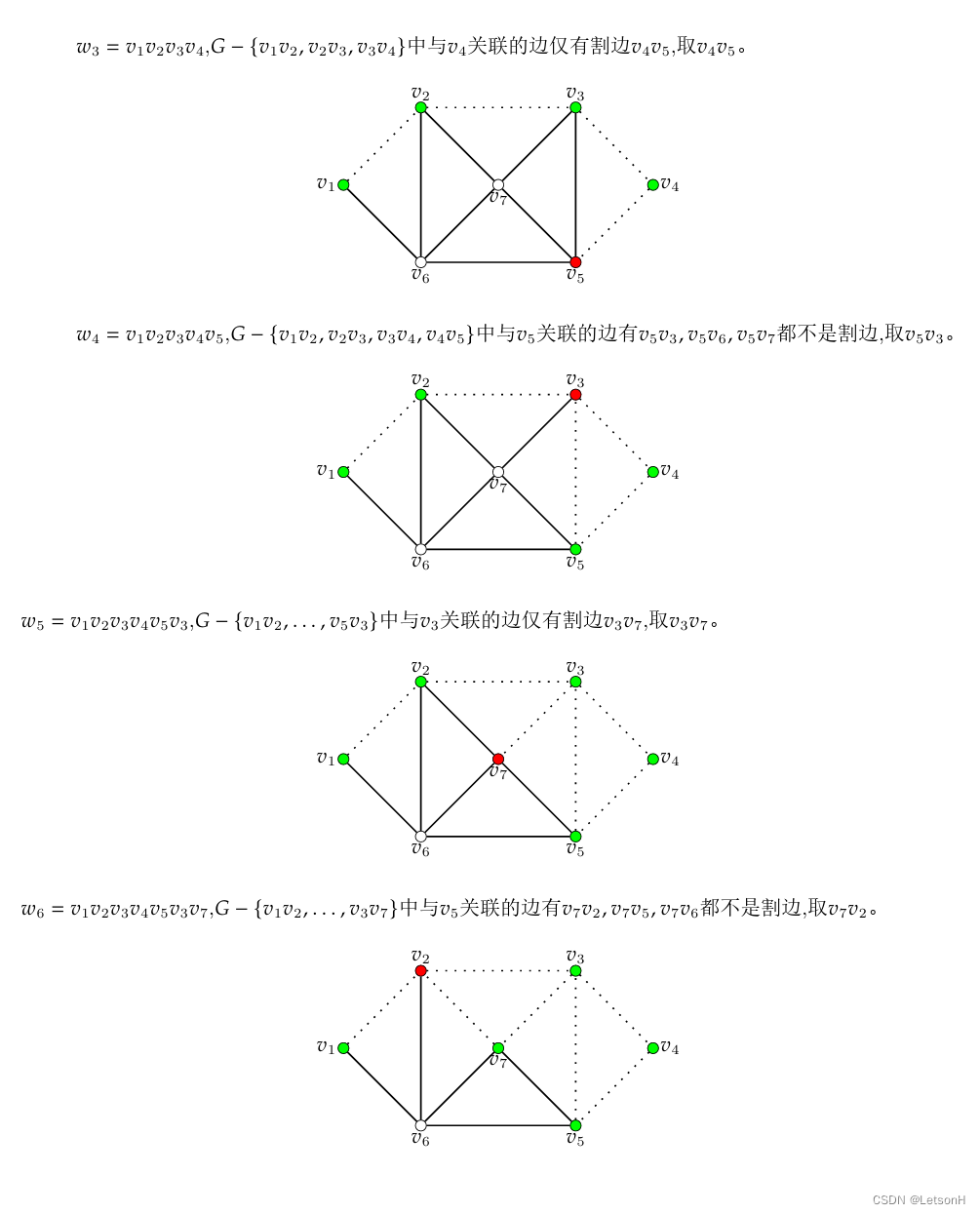
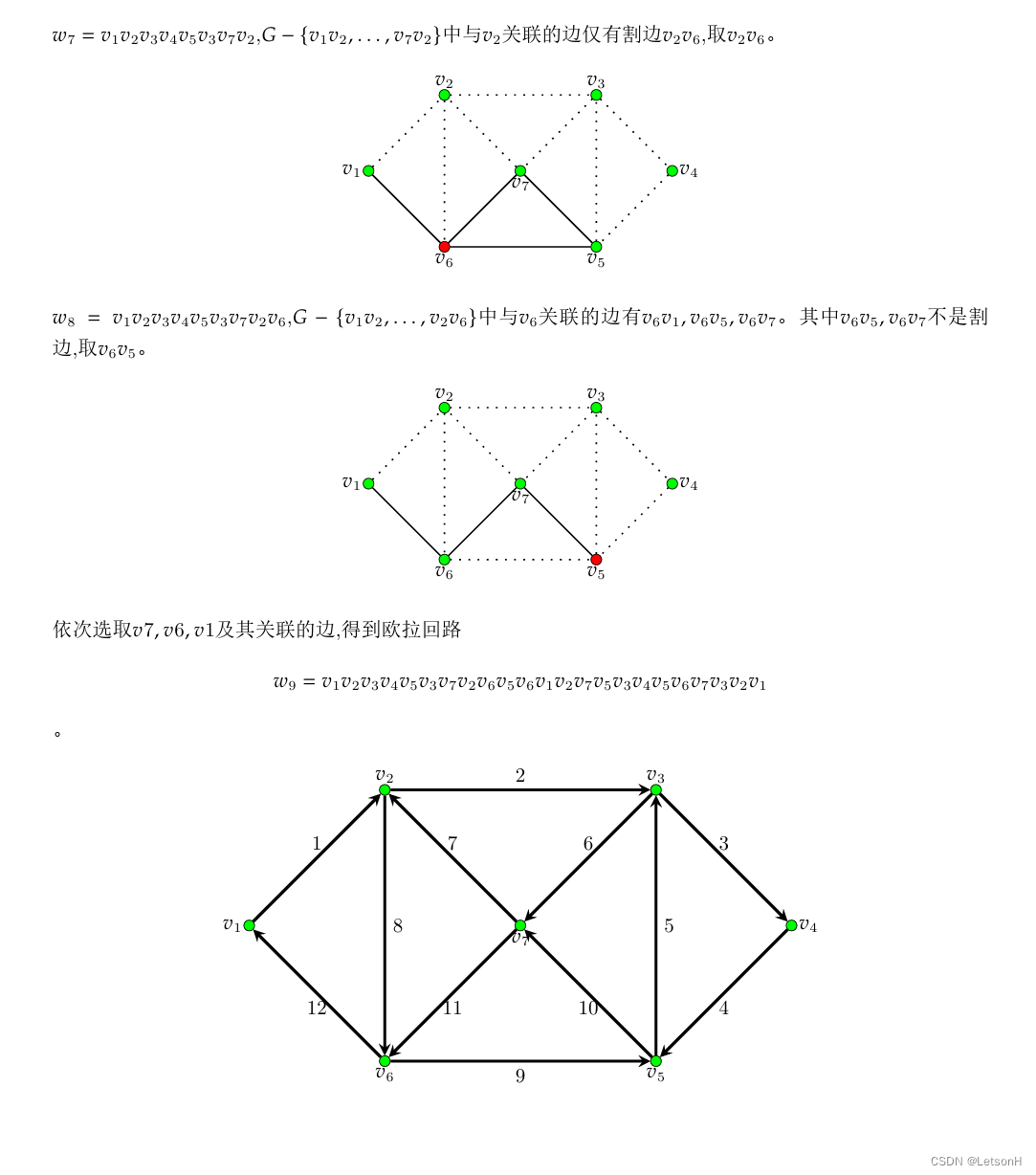
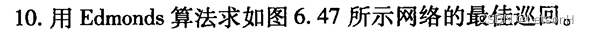
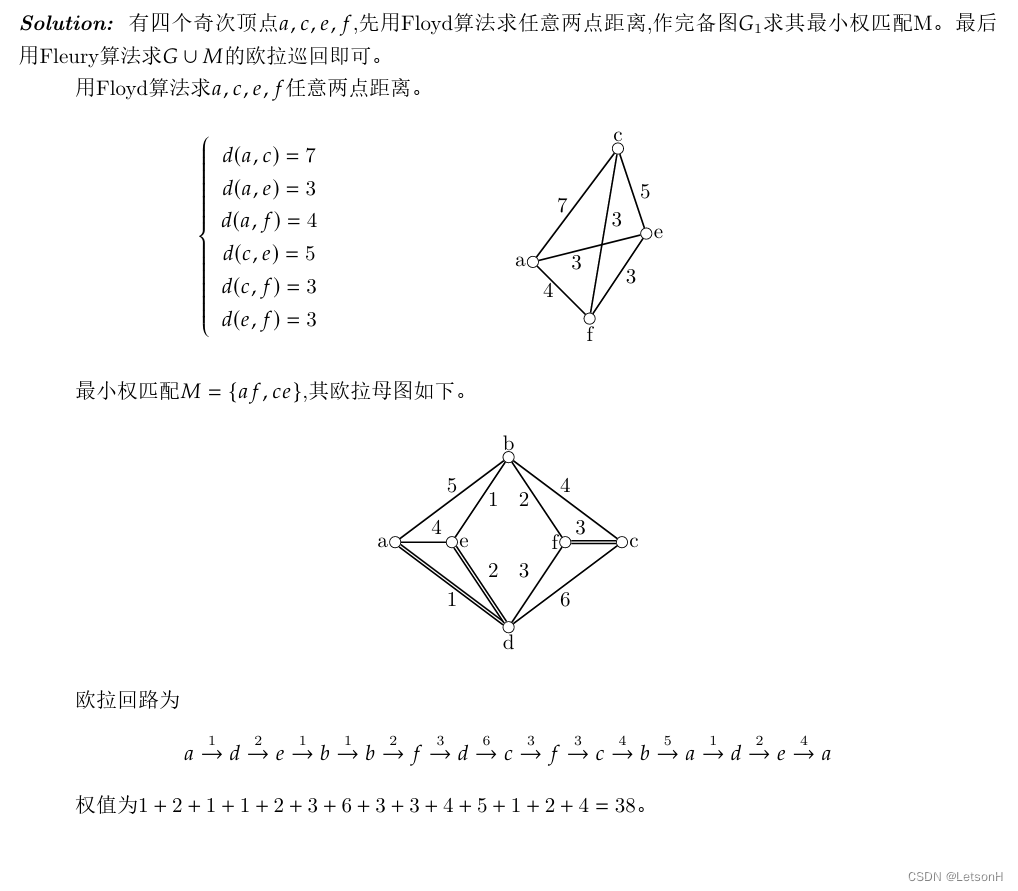
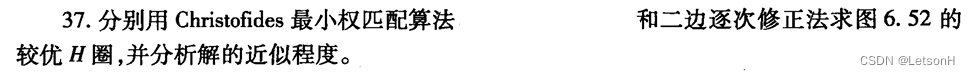
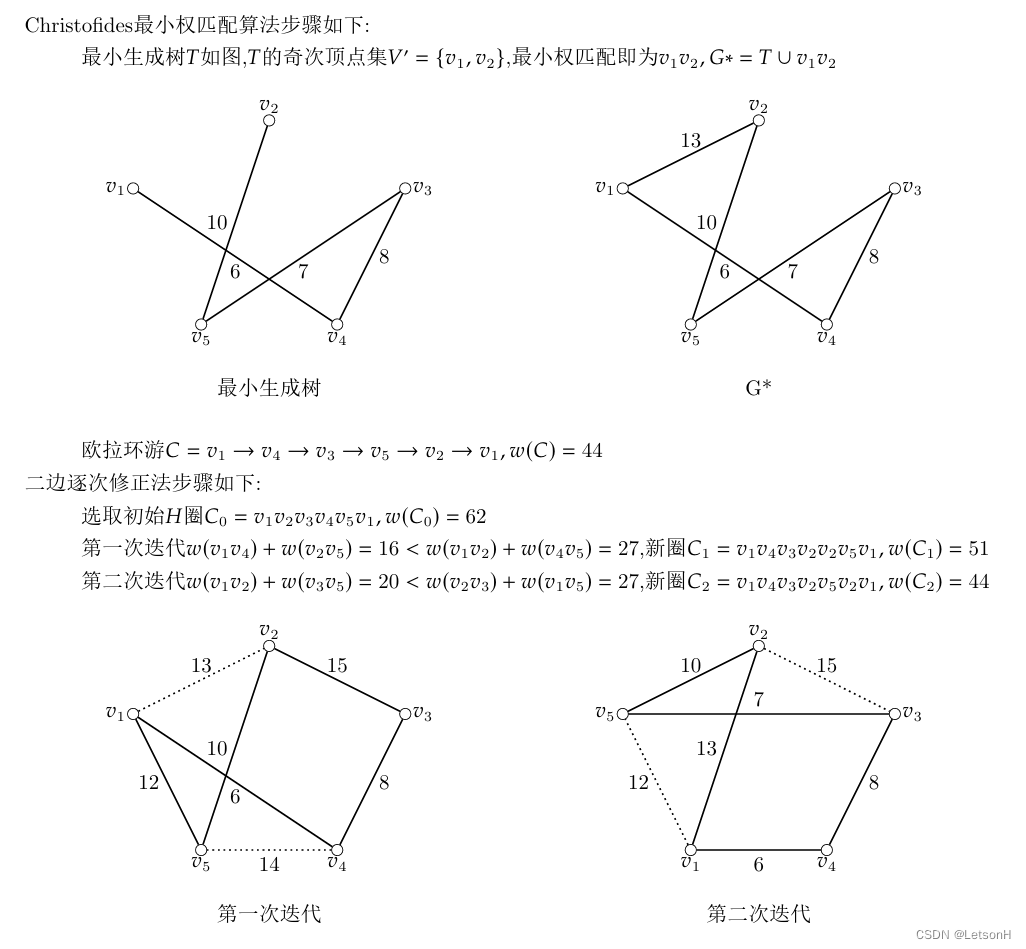
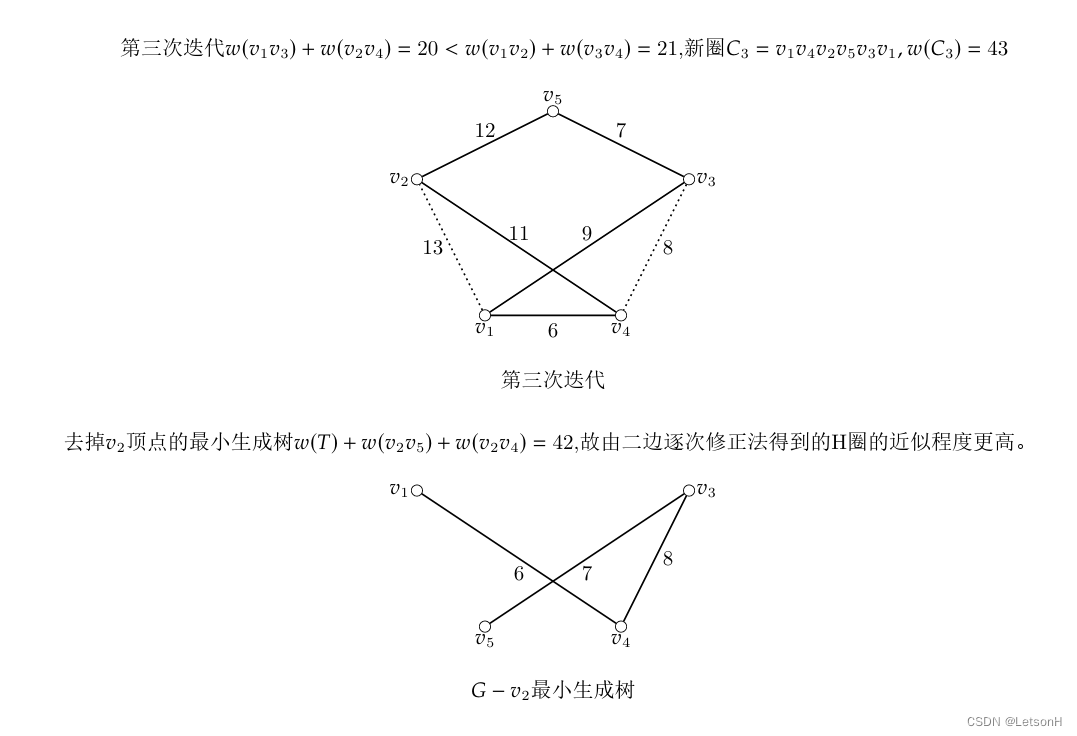
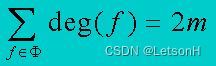


 当且仅当G是连通的。
当且仅当G是连通的。