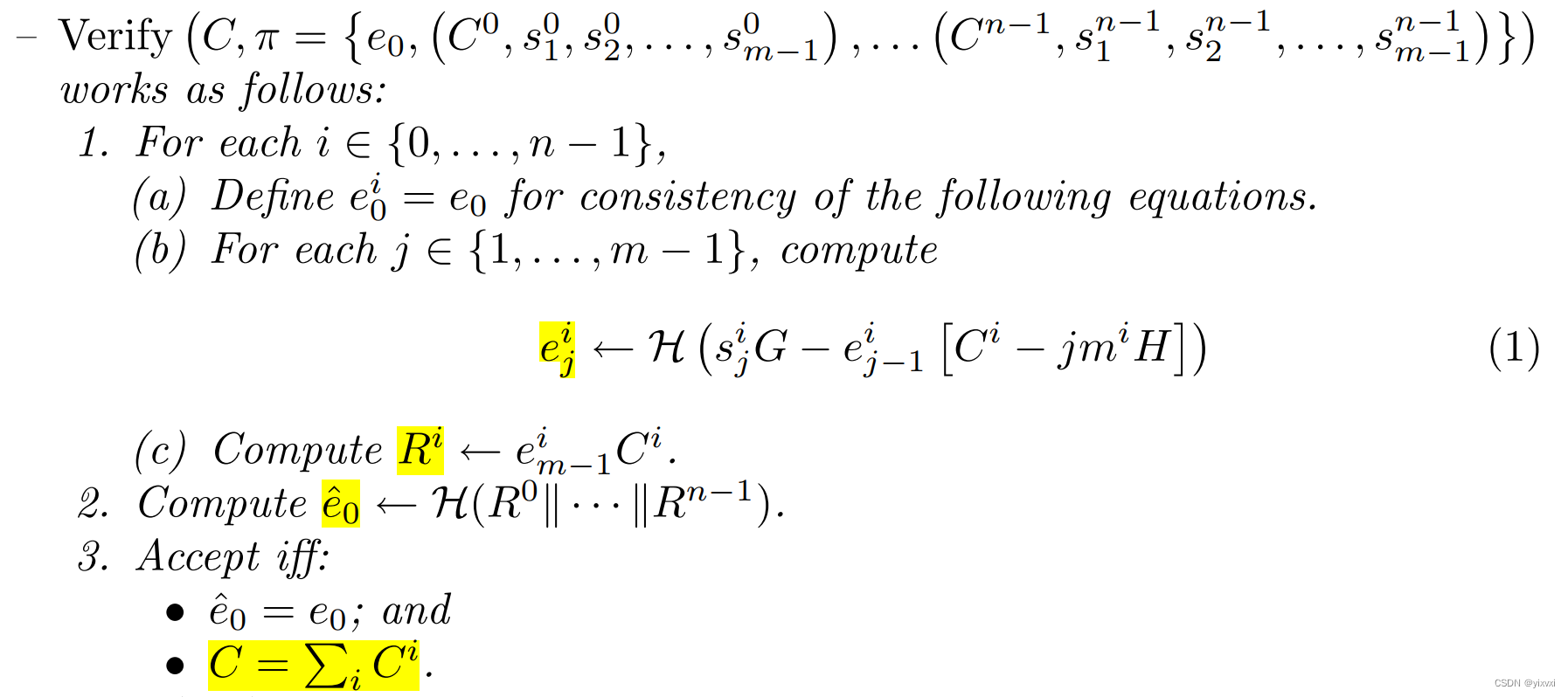- 描述了一种称为“保密交易”的方案,该方案模糊了所有UTXO的金额,同时保持了不创建或销毁硬币的公共可验证性。
- 进一步将此方案扩展到“保密资产”,一种单一的基于区块链的分类帐可以跟踪多种资产类型的方案。
- 将保密交易扩展到不仅模糊输出金额,还模糊其资产类型,从而提高所有资产的隐私和可替代性。
- Preliminaries:定义交易模型,承诺(特性)、范围证明(安全性定义)
- 改进的Confidential Transactions:将交易中的明文金额改成承诺的金额,改进范围证明,并证明改进交易的安全性和性能优化。
- Confidential Assets:机密资产协议。
Preliminaries
输入输出模型
(还需要coinbase交易,有输出但没有输入;在本文的目的中,它们可以被视为具有负费用的交易。)
用于隐藏交易数量的同态承诺
M
=
Z
q
M=Zq,承诺空间
C
≃
M
P
P
- Setup:
⋅
→
P
P
⋅→PP - Commit:
P
P
×
M
×
M
→
C
mathcal{PP} times mathcal M times mathcal M rightarrow mathcal C
PP×M×M→C - Open:
P
P
×
M
×
M
×
C
→
{
u
,
f
a
l
}
mathcal{PP} times mathcal M times mathcal M times mathcal C rightarrow {true, false}
PP×M×M×C→{true,false}
满足以下条件(对于p
p
←
S
t
u
p
pp←Setup): - 正确性:对于所有
(
,
r
)
∈
M
×
M
(m, r) in mathcal M times mathcal M
(m,r)∈M×M,O
p
e
n
(
p
p
,
m
,
r
,
C
m
m
i
t
(
p
p
,
m
,
r
)
)
Open(pp, m, r, Commit(pp, m, r))
Open(pp,m,r,Commit(pp,m,r))接受; - (加)同态性:如果
O
p
e
n
(
p
p
,
m
1
,
r
1
,
C
1
)
Open(pp,m1,r1,C1) 和O
p
e
n
(
p
p
,
m
2
,
r
2
,
C
2
)
Open(pp,m2,r2,C2) 都接受,那么O
p
e
n
(
p
p
,
m
1
+
m
2
,
r
1
+
r
2
,
C
1
+
C
2
)
Open(pp, m_1 + m_2, r_1 + r_2, C_1 + C_2)
Open(pp,m1+m2,r1+r2,C1+C2) 也接受。
定义3. 如果对于所有
m
≠
m
′
∈
M
m neq m’ in mathcal M
m=m′∈M,以及所有
r
,
r
′
∈
M
r, r’ in mathcal M
r,r′∈M,都有
O
p
e
n
(
m
,
r
,
C
m
m
i
t
(
m
′
,
r
′
)
)
Open(m,r,Commit(m′,r′))拒绝,那么承诺是完美绑定的。
A
mathcal A
A,使得
A
mathcal A
A 产生
(
m
′
,
r
′
)
(m’, r’)
(m′,r′) 且
m
′
≠
m
m’ neq m
m′=m 以至于
O
p
e
n
(
m
,
r
,
C
o
m
m
i
t
(
m
′
,
r
′
)
)
Open(m, r, Commit(m’, r’))
Open(m,r,Commit(m′,r′)) 接受的概率是可以忽略的,则承诺是计算上绑定的。
p
p
pp
pp 和
m
1
≠
m
2
m_1 neq m_2
m1=m2,分布
U
1
=
{
C
:
C
←
C
o
m
m
i
t
(
p
p
,
m
1
,
r
)
,
r
←
M
}
U_1 = {C : C leftarrow Commit(pp, m_1, r), r leftarrow M}
U1={C:C←Commit(pp,m1,r),r←M}
U
2
=
{
C
:
C
←
C
o
m
m
i
t
(
p
p
,
m
2
,
r
)
,
r
←
M
}
U_2 = {C : C leftarrow Commit(pp, m_2, r), r leftarrow M}
U2={C:C←Commit(pp,m2,r),r←M}
是(相等的,统计上无法区分的,计算上无法区分的),那么承诺方案是(完全,统计上,计算上)隐藏的。
本文使用Pedersen承诺,它是满足计算绑定,完美隐藏的同态承诺
Pedersen承诺
定义5. 取
M
=
Z
q
mathcal M = mathbb Z_q
M=Zq,
C
mathcal C
H
mathcal H
- Setup 接受一个带有区别生成元
(
G
,
G
)
(mathcal G, G)
(G,G) 的循环群,以及辅助输入α
α。它计算H
=
H
(
α
)
H = mathcal H(alpha)
H=H(α) 并输出p
p
=
{
G
,
G
,
H
}
pp = {mathcal G, G, H}
pp={G,G,H}。 -
C
o
m
m
i
t
(
m
,
r
)
Commit(m, r)
Commit(m,r) 输出m
H
+
r
G
mH + rG
mH+rG。 -
O
p
e
n
(
m
,
r
,
C
)
Open(m, r, C)
Open(m,r,C) 接受当且仅当C
=
m
H
+
r
G
C = mH + rG
C=mH+rG。
(原始的Pedersen方案使用均匀随机生成元G
,
H
G, H
G,H,而不是将H
H
H 视为哈希函数的输出。在随机预言模型中,这两者是等价的。)
range proof
定义6. 给定如上所述的同态承诺方案,以及
0
≤
A
≤
B
≤
q
[
A
,
B
]
[A, B]
-
P
r
o
e
[
A
,
B
]
Prove_{[A,B]}
Prove[A,B]:P
P
×
M
→
C
×
M
×
S
mathcal{PP times M rightarrow C times M times S}
PP×M→C×M×S,接受一个值并生成对该值的承诺,同时生成打开信息和相关的范围证明。 -
V
e
r
i
f
[
A
,
B
]
Verify_{[A,B]}
Verify[A,B]:P
P
×
C
×
S
→
{
t
r
u
e
,
f
a
l
s
e
}
mathcal{PP times C times S} rightarrow {true, false}
PP×C×S→{true,false},接受一个承诺和范围证明,要么接受要么拒绝。
其中S
mathcal S
S 表示可能的范围证明空间。要求对于所有∈
[
A
,
B
]
v in [A, B]
v∈[A,B],(
C
,
r
,
π
)
←
P
r
o
v
e
[
A
,
B
]
(
v
)
(C, r, pi) leftarrow Prove_{[A,B]}(v)
(C,r,π)←Prove[A,B](v),V
e
r
i
f
[
A
,
B
]
(
C
,
π
)
a
n
O
p
e
n
(
v
,
r
,
C
)
Verify_{[A,B]}(C, pi) and Open(v, r, C)
Verify[A,B](C,π) and Open(v,r,C)都接受。
0
≤
A
≤
B
≤
q
0 leq A leq B leq q
[
A
,
B
]
[A, B]
[A,B]内,如果对于任何输出
(
C
,
π
)
∈
C
×
S
A
mathcal A
A使得
V
e
r
i
f
y
(
C
,
π
)
Verify(C, pi)
B
B
B,它在给定对
A
A
(
v
,
r
)
(v, r)
(v,r),使得
v
∈
[
A
,
B
]
v in [A, B]
v∈[A,B] 并且
O
p
e
n
(
v
,
r
,
C
)
Open(v, r, C)
[
A
,
B
]
[A, B]
[A,B]中的金额的open排除了对
[
A
,
B
]
[A, B]
[A,B]以外的任何金额的open。根据定义7,给定一个具有有效范围证明
π
π
π的承诺
C
C
C
的
o
p
e
n
(
v
,
r
)
C的open信息(v,r)”,即使不知道它(因为这个知识原则上可以由模拟器获得)。特别是,任何要求对手提供承诺公开信息的安全证明,如果公开信息被范围证明所取代,将继续有效。)
Confidential Transactions
Rangeproofs
[
0
,
m
n
−
1
]
[0,m^n – 1]
[0,mn−1]上对Pedersen承诺进行有效的范围证明,其总大小与
1
+
n
m
1 + nm
1+nm成比例,使用了一种基于民间传说的基于二进制分解(bit–decomposition)的范围证明变体,其中数字以基
m
m
[
0
,
m
−
1
]
[0,m – 1]
使用Borromean Ring Signatures的一种变体。
Schoenmakers [19]描述了一种使用每个数字的零知识OR证明的简单基于
b
b
b数位的范围证明。我们的工作基于这个范围证明,并做出以下更改:我们的OR证明基于Borromean Ring Signatures:
定义9(Back-Maxwell Rangeproof )。考虑一个Pedersen承诺方案,其中包含生成器
G
、
H
G、H
G、H,并且
H
:
C
→
M
mathcal{H:C → M}
n
n
n个规模为
m
m
m的环。
e
0
e_0
e0作为Borromean签名中多个环相结合的部分,下面的第二大部分是构建每个环内部结构。特别地对于
v
i
=
0
v^i=0
vi=0,将其处理成与其他环不可区分的项;而对于
v
i
≠
0
v^ineq 0
vi=0的部分和原始Borromean签名几乎相同,除了对
e
j
i
e_j^i
eji的定义)

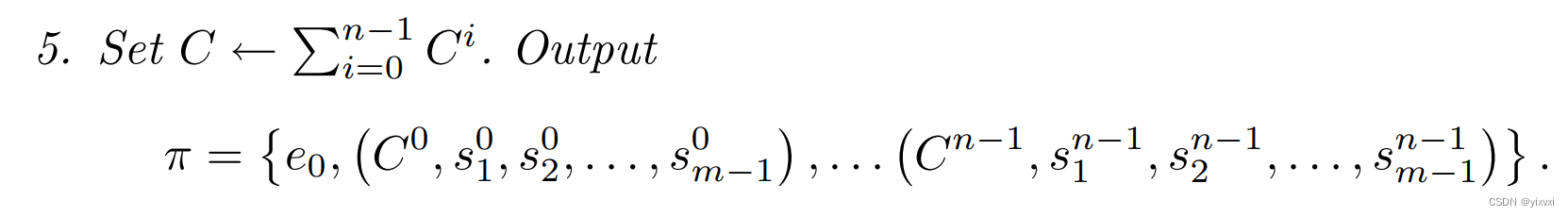
正确性:
- 对于
v
i
≠
0
v^ineq0
vi=0的项,j
=
{
1
,
.
.
.
,
v
i
−
1
}
j={1,…,v^i-1}
j={1,…,vi−1}的e
j
i
e_j^i
eji和R
i
R^i
Ri的计算直接按定义恢复。 - 对于
v
i
≠
0
v^ineq0
vi=0的项,j
=
v
i
j=v^i
j=vi的项,
e
v
i
i
=
H
(
s
v
i
i
G
−
e
v
i
−
1
i
[
C
i
−
v
i
m
i
H
]
)
=
H
(
i
G
+
e
v
i
−
1
i
r
i
G
−
e
v
i
−
1
i
[
m
i
v
i
H
+
r
i
G
−
v
i
m
i
H
]
)
=
H
(
i
G
)
e_{v^i}^i=mathcal H(s_{v^i}^iG-e_{{v^i}-1}^i[C^i-{v^i}m^iH])=mathcal H(k^iG+e^i_{v^i-1}r^iG-e_{{v^i}-1}^i[m^iv^iH+r^iG-{v^i}m^iH])=mathcal H(k^iG)
evii=H(sviiG−evi−1i[Ci−vimiH])=H(kiG+evi−1iriG−evi−1i[miviH+riG−vimiH])=H(kiG)符合定义。 - 对于
v
i
=
0
v^i=0
vi=0的项,则需让其也符合v
i
≠
0
v^ineq0
vi=0中的定义:-
e
j
i
=
H
(
s
j
i
G
−
e
j
−
1
i
[
C
i
−
j
m
i
H
]
)
=
H
(
(
j
i
+
0
i
e
j
−
1
i
e
m
−
1
i
)
G
−
e
j
−
1
i
[
k
0
i
e
m
−
1
i
G
−
j
m
i
H
]
)
=
H
(
k
j
i
G
+
e
j
−
1
i
m
i
j
H
)
e_j^i=mathcal H(s_j^iG-e_{j-1}^i[C^i-jm^iH])=mathcal H((k_j^i+frac{k_0^ie_{j-1}^i}{e_{m-1}^i})G-e_{j-1}^i[frac{k_0^i}{e_{m-1}^i}G-jm^iH])=mathcal H(k_j^iG+e_{j-1}^im^ijH)
eji=H(sjiG−ej−1i[Ci−jmiH])=H((kji+em−1ik0iej−1i)G−ej−1i[em−1ik0iG−jmiH])=H(kjiG+ej−1imijH) -
R
i
=
e
m
−
1
i
C
i
=
e
m
−
1
i
R
i
e
m
−
1
i
=
k
0
i
G
R^i=e_{m-1}^iC^i=e_{m-1}^ifrac{R^i}{e_{m-1}^i}=k_0^iG
Ri=em−1iCi=em−1iem−1iRi=k0iG
-
(关于这个方案对原始的Borromean环签名的改进可参考比对:https://blog.csdn.net/jiongxv/article/details/125014841)
- 没有
s
0
i
s^i_0
s0i值,这在Borromean环签名构造中用于计算e
^
0
hat e_0
e^0,从而在总体证明中节省i
i
i个标量。 - 承诺
C
i
C^i
Ci不再包含在任何哈希中(在计算子承诺到数字(
m
−
1
)
(m−1)
(m−1)时,如Prove算法的第4(a)ii步所示,这是必要的)。不幸的是,由此产生的构造在一般情况下不再是一个安全的环签名;安全性的证明取决于所有密钥都是绑定承诺而不是任意的公钥。
(省略部分:证明这个改进的range proof算法仍然是安全的,利用前面给出的定理7~8)
Confidential Transactions
修改比特币交易的定义(定义1)。
定义10。我们将机密交易定义为以下数据:
- 一个输出列表,包含验证密钥、对金额的Pedersen承诺和Back-Maxwell范围证明,证明它位于区间
[
0
,
2
n
−
1
]
[0, 2^n −1]
[0,2n−1],其中n
n
n明显小于承诺值群的比特长度。 - 一个输入列表,这些输入是对其他交易输出的明确引用,并使用这些输出的验证密钥进行签名。
- 一个明确列出的费用
f
f
f。
定义11。验证方程是:输入金额减去输出金额等于费用(将这些金额视为承诺时,乘以H)。
通过输入签名实现付款授权,这与比特币相同,但在本文中没有详细讨论。然而,我们需要论证这种变化不会允许无效地创建硬币。
- 费用为
f
f
f,输入对金额{
I
i
}
i
=
0
k
{I_i}^k_{i=0}
{Ii}i=0k进行承诺,输出对金额{
O
i
}
i
=
0
l
{O_i}_{i=0}^{l}
{Oi}i=0l进行承诺。 - 假设
k
+
l
+
1
<
∣
C
∣
/
R
k + l + 1 < |mathcal C|/R
k+l+1<∣C∣/R,其中输出范围证明是在范围[
0
,
R
−
1
]
[0,R−1]
[0,R−1]内的,且f
∈
[
0
,
R
−
1
]
f ∈ [0, R−1]
f∈[0,R−1]
(通常,群阶为C
≈
2
256
,
R
≈
264
mathcal C≈2^{256},R≈264
C≈2256,R≈264,因此这一要求在实践中是不可能违背的。) - 如果范围证明是proving的且承诺是绑定的,那么
{
O
i
}
{O_i}
{Oi}的任何子集都不会承诺多于∑
i
=
0
k
I
i
−
f
sum^k_{i=0} I_i − f
∑i=0kIi−f
观察到,简单地论证
∑
i
=
0
k
I
i
−
f
=
∑
i
=
0
l
O
i
sum^k_{i=0} I_i − f=sum_{i=0}^lO_i
∑i=0kIi−f=∑i=0lOi是不够的:例如,在输入和费用为零的情况下,攻击者可以提交两个输出量{1,−1},并且即使整个方程平衡,也可以凭空创建一个硬币。
Proof:
- 由于所有的范围证明都是有效的,且承诺是绑定的,对于每个
i
i
i,我们有0
≤
O
i
≤
R
0 ≤ O_i ≤ R
0≤Oi≤R。对于输入也是一样的,它们是先前(有效)交易的输出。 - 接下来,由于输入承诺减去输出承诺等于
f
H
fH
fH,我们有∑
i
=
0
k
I
i
−
f
−
∑
i
=
0
l
O
i
≡
0
(
m
o
∣
C
∣
)
sum_{i=0}^kI_i − f − sum_{i=0}^l O_i ≡ 0 (mod~|mathcal C|)
∑i=0kIi−f−∑i=0lOi≡0(mod ∣C∣),或者说存在某个整数m
m
m:
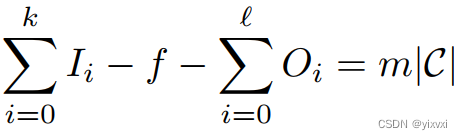
- 因为
k
+
l
+
1
<
∣
C
∣
/
R
k + l + 1 < |mathcal C|/R
k+l+1<∣C∣/R,根据每一项的边界,我们可以把方程左边的边界设为:
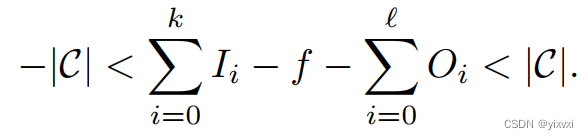
但这意味着m
=
0
m = 0
m=0,即输入金额加到输出金额上(加上fee)=0。 - 最后,由于所有的输出量都是正的,输出的每个子集的和必须小于或等于
∑
i
=
0
k
I
i
−
f
sum^k_{i=0} I_i − f
∑i=0kIi−f,如所希望的那样。证毕。
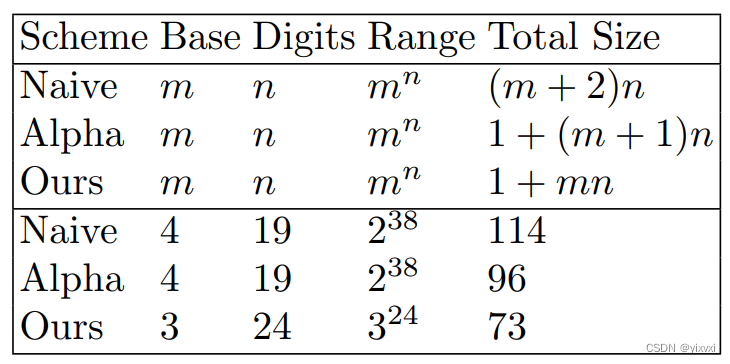
Performance
考虑一个群
G
mathcal G
G,其中标量和群元素都在1个空间单位中编码(实际上是32字节或256位)。我们对比了三种方案:
- 一种使用每个数字单独的AOS环签名的朴素的民间距离证明方案;
- 一种是使用在Elements Alpha[2]中实现的Borromean环签名[15];
- 本文方案。
进行了渐进比较,也看了具体情况2
38
≈
3
24
2^{38}≈3^{24}
238≈324。虽然naive和Alpha方案在基数4下是空间最优的,但我们的方案在基数3下是空间最优的。
Confidential Assets
给出资产标签的定义(承诺的形式)
资产承诺和担保证明
定义12。给定某个资产描述A(其精确形式在第4.4节中给出),相关的资产标签是元素
H
A
∈
G
H_A ∈ mathcal G
HA∈G,它是通过使用A作为辅助输入执行Pedersen承诺Setup得到的。
H
A
H_A
HA,一个(暂时的)资产承诺是形式为
H
=
H
A
+
r
G
H = H_A + rG
H=HA+rG的点,其中
r
r
在下一节中,使用这些资产承诺来代替Pedersen承诺中的生成元
H
H
H。下面的定理证明了这一点。
定理4。设
H
H
H是对资产标签
H
A
H_A
HA的资产承诺,
C
C
C是一个Pedersen承诺,使得
O
p
e
n
H
(
v
,
r
,
C
)
Open_H(v, r, C)
OpenH(v,r,C)接受。那么如果
H
A
=
H
+
s
G
H_A = H + sG
HA=H+sG,那么
O
p
e
n
H
A
(
v
,
r
−
s
v
,
C
)
Open_{H_A}(v, r − sv, C)
OpenHA(v,r−sv,C)也会接受。
推导一下:
O
p
e
n
H
(
v
,
r
,
C
)
=
C
=
v
H
+
r
G
=
v
(
H
A
−
s
G
)
+
r
G
=
v
H
A
+
(
r
−
s
v
)
G
Open_H(v, r, C)=C=vH+rG=v(H_A-sG)+rG=vH_A+(r-sv)G
OpenH(v,r,C)=C=vH+rG=v(HA−sG)+rG=vHA+(r−sv)G
这个定理是直接的,它意味着对某个资产承诺作为生成元的Pedersen承诺也是对同一金额以底层资产标签作为生成元的Pedersen承诺。此外,任何知道盲因子
s
s
s和对于一个生成元的open信息的人都可以确定对于另一个生成元的open信息。
这样的Pedersen承诺不仅对承诺的金额进行承诺,还对底层资产标签进行承诺,具体如下:
定理5。如果存在一个可以在以下游戏中以非可忽略概率取胜的ppt算法
A
mathcal A
A,那么存在一个模拟器
B
mathcal B
G
mathcal G
G)。
-
A
mathcal A
A调用S
e
t
u
p
i
Setup_i
Setupi生成资产标签H
i
H_i
Hi,对于i
=
0
,
1
,
.
.
.
,
n
i = 0, 1, … , n
i=0,1,…,n。 -
A
mathcal A
A生成承诺C
i
C_i
Ci和打开(
v
i
,
r
i
)
(v_i, r_i)
(vi,ri),使得对于i
=
1
,
.
.
.
,
n
i = 1, … , n
i=1,…,n,O
p
e
n
i
(
v
i
,
r
i
,
C
i
)
Open_i(v_i, r_i, C_i)
Openi(vi,ri,Ci)接受。 -
A
mathcal A
A生成打开(
v
,
r
)
(v, r)
(v,r),使得v
≠
0
v ≠ 0
v=0且O
p
e
n
0
(
v
,
r
,
∑
i
=
1
n
C
i
)
Open_0(v, r, sum^n_{i=1} C_i)
Open0(v,r,∑i=1nCi)接受。
(证明略)
根据Definition 7后面的评论,如果要求敌手产生范围证明而不是open信息,则相同的定理成立。
我们将向所有交易输出附加新的随机资产承诺,并且我们需要一种在不揭示映射的情况下链接输入和输出的方法。以下工具将是必不可少的。
定义14。资产满射证明(ASP)方案包括以下算法。
- Prove接受“输入”资产承诺的集合
{
H
i
}
i
=
1
n
{H_i}^n_{i=1}
{Hi}i=1n,一个“输出”承诺H
=
H
i
∗
+
r
G
H = H_{i^∗} + rG
H=Hi∗+rG(其中1
≤
i
∗
≤
n
1 ≤ i^∗ ≤ n
1≤i∗≤n),以及r
r
r。它输出一个证明π
π
π。 - Verify接受集合
{
H
i
}
i
=
1
n
{H_i}^n_{i=1}
{Hi}i=1n,H
H
H和一个证明π
π
π,然后要么接受要么拒绝。
我们经常说ASP是从输入承诺的集合
{
H
i
}
{H_i}
{Hi}到输出承诺
H
H
H的。
定义15。如果由Prove算法生成的证明
π
π
π是盲因子
r
r
这很容易通过环签名构造,环签名是其其中一个密钥的zkPoK,例如AOS环签名。
定义16。AOS ASP如下:
- Prove计算
i
=
1
,
.
.
.
,
n
i = 1,…,n
i=1,…,n的n
n
n个差值H
−
H
i
H −H_i
H−Hi(其中之一将是r
r
r),并使用这些差异计算一个空消息的环签名。
π
π
π就是这个签名。 - Verify计算相同的差值们并验证环签名。
如果底层的AOS环签名方案是zkPoK,那么AOS ASP是安全的,这是显而易见的 。
Confidential Assets
定义17。机密资产交易是以下数据:
- 一个输入列表,有两种形式之一:
- 一个输出列表,包含:
- 一个fee
{
(
f
i
,
H
i
)
}
i
=
1
n
{(f_i, H_i)}^n_{i=1}
{(fi,Hi)}i=1n,明确列出。
∑
i
=
1
n
f
i
H
i
sum^n_{i=1} f_iH_i
∑i=1nfiHi,而不仅仅是
f
H
fH
fH。
Performance
在3.3节中,我们描述了附加到每个交易输出的范围证明的大小。这对于机密资产是不变的,但我们还需要两个额外的数据:资产承诺和显示此承诺合法的ASP。
(例如,一个资产标签
H
A
H_A
HA的承诺
H
H
H,AOS ASP用环签名构造,单个环签名规模
n
+
1
n+1
n+1)
在3.3节的单元中,资产承诺的规模为
1
1
1,ASP的规模为
n
+
1
n + 1
n+1,其中
n
n
m
m
m个输出和
n
n
n个输入的整个交易,因此附加数据的大小为
m
(
n
+
2
)
m(n + 2)
m(n+2)。
我们可以通过以隐私为代价来改进这一点:使用较弱形式的ASP来改进,
n
=
3
n=3
n=3。那么附加的数据将只花费
5
m
5m
Issuance 发行
在区块链的上下文中,希望确保任何资产A只能被使用一次,以确保无法通过多个独立的发行来膨胀资产。将发行与UTXO的花费关联起来,并确保每个特定UTXO最多只有一个发行,可以实现这种唯一性属性。将花费的UTXO的明确引用与发行者指定的值一起哈希,即Ricardian contract hash,生成Pedersen承诺的辅助输入
A
A
A。
定义18。给定要花费的输入
I
I
I,它本身是对另一笔交易输出的明确引用,以及发行者指定的Ricardian contract
C
C
C,资产熵
E
E
E定义为
H
a
s
h
(
H
a
s
h
(
I
)
∣
∣
H
a
s
h
(
C
)
)
Hash(Hash(I)||Hash(C))
Hash(Hash(I)∣∣Hash(C))。
Ricardian contract是一份机器可解析的法律文件,规定了资产的使用条件,尤其是赎回条件。这样的合同可能如何设计或执行的详细信息超出了本文的范围。在这里重要的是这样的文件存在,并且其哈希在发行资产时被不可撤销地承诺。
定义19。给定资产熵
E
E
E,资产标签是通过使用
H
a
s
h
(
E
∣
∣
0
)
Hash(E||0)
Hash(E∣∣0)作为辅助输入执行Pedersen承诺设置得到的元素
H
A
∈
G
H_A ∈ mathcal G
HA∈G。每个非coinbase交易输入最多可以关联一个新的资产发行:
定义20。资产发行输入包括:
- 一个UTXO花费
I
I
I(解释为同一交易的非发行输入); - 一个Ricardian合同
C
C
C; - 一个初始发行的显式值
v
0
v_0
v0,或者Pedersen承诺H
H
H和BackMaxwell范围证明P
0
P_0
P0; - 一个布尔字段,指示是否允许重新发行。重新发行将在下节中解释。
重新发行和能力令牌
定义21。给定资产熵
E
E
E,资产重新发行能力是通过使用
H
a
s
h
(
E
∣
∣
1
)
Hash(E||1)
Hash(E∣∣1)作为辅助输入执行Pedersen承诺设置得到的元素
H
A
∈
G
H_A ∈ mathcal G
HA∈G。
支持重新发行的资产在其资产发行输入中指示这一点,并且交易包含一个额外的金额为
1
1
1的输出,承诺到资产标签
H
A
H_A
HA。
通过这种方式,资产标签与相应的重新发行能力相关联,持有这种能力的人可以通过揭示能力的盲因子以及原始资产熵来主张他们的重新发行权利。
定义22。资产重新发行输入包括对包含资产重新发行能力的UTXO的花费;原始资产熵E;正在花费的UTXO的资产承诺的盲因子;以及显式的重新发行金额vi,或者Pedersen承诺H和Back-Maxwell范围证明Pi。
这种重新发行机制是通用基于能力的身份验证方案的一个特定实例。可以使用相同的方案来定义控制对其他受限操作的访问的能力。
Performance
与机密交易不同,在机密资产中,每个输出都必须附带范围证明,而且每个机密资产输出还必须有一个资产标签和资产满射证明。与第3.3节一样,我们认为曲线点和标量具有相同的大小。
对于一个金额在范围
[
0
,
m
n
)
[0,m^n)
[0,mn)内并引用A个资产的输出,因此范围证明和ASP的总大小是
(
1
+
m
n
)
+
(
2
+
A
)
(1+mn)+(2+A)
(1+mn)+(2+A),其中第一个术语是范围证明的贡献,第二个是资产标签和ASP的贡献。
(范围证明
1
+
m
n
1+mn
1+mn,资产标签1,ASP
A
+
1
A+1
A+1)
对于一个
[
0
,
3
24
)
[0,3^{24})
[0,324)范围证明和三个输入的原型示例,总共是78个标量,或19968位。
(
1
+
3
×
24
+
2
+
3
=
78
1+3times24+2+3=78
1+3×24+2+3=78)(注意不要把机密资产和机密交易混为一谈)
“Small Assets” and “Big Assets”
- Big Assets:用ASP绑定输入与输出资产类型,使得机密资产能够在支持无限多种资产类型的区块链上运行,这些资产类型可以在链定义之后添加。
- Small Assets:另一种方案,适用于一小组固定的资产标签,是在链的开始定义资产标签,并使每个输出包含对全局资产标签列表的ASP。
- 还可以通过在每个交易中选择其输出具有ASP的资产标签子集来使用中间方案,具有全局动态资产列表。一般来说,有很大的空间可以根据特定用例的ASP大小和隐私之间的最佳权衡进行调整。
Future Research
- 范围证明效率。
- ASP效率。限制输入集规模可以提高效率,但这会以用户隐私为代价,最好是避免这种权衡。
- 聚合范围证明。如果能够聚合范围证明(例如,将
C
1
C_1
C1和C
2
C_2
C2承诺在[
0
,
2
n
−
1
]
[0,2^n − 1]
[0,2n−1]中的值的证明合并成一个证明,证明C
1
+
C
2
C_1 + C_2
C1+C2承诺在[
0
,
2
n
+
1
−
1
]
[0,2^{n+1} − 1]
[0,2n+1−1]中的值),这也将提高基于区块链的系统的效率,因为证明可以放置在一个Merkle汇总树中,其节点包含其子节点的聚合范围证明。然后,验证者只需检查根节点,以确保整个树不会导致通货膨胀,延迟对个别输出上的证明的检查,直到这些输出被花费。 - 量子抗性。本文中描述的原语都依赖于椭圆曲线离散对数假设,这被认为在量子对手面前是不安全的。量子困难性的类似物需要替代Pedersen承诺、ASP使用的环签名以及范围证明。
原文地址:https://blog.csdn.net/jiongxv/article/details/134463581
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。
如若转载,请注明出处:http://www.7code.cn/show_32704.html
如若内容造成侵权/违法违规/事实不符,请联系代码007邮箱:suwngjj01@126.com进行投诉反馈,一经查实,立即删除!