.
镜头畸变对比
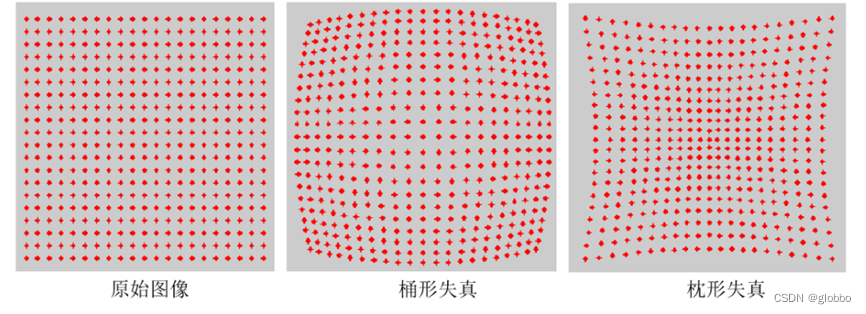
镜头畸变包含了径向畸变和切向畸变,径向畸变主要由透镜产生,它的效应主要有两种:枕形和桶形,如图所示。在 CMOS 中心(光学中心)的畸变为 0,随着向边 缘移动,畸变越来越严重。切向畸变来自于透镜安装的整个过程,因为安装时很难保证透镜和成像平面平行。
具体的公式halcon采用的和张正友是一样的:
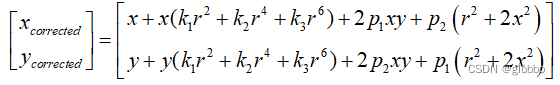
而Opencv最新版本的公式如下:
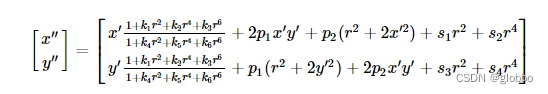
可以看到,右边径向畸变系数k,halcon和OpenCV是不一样的,但形式一致,切向是相同的,并且OpenCV还多了
(
1
s
2
s
3
s
4
)
(s_{1}s_{2}s_{3}s_{4})
(s1s2s3s4)四个参数。
经过对比验证,最关键的还不是这个,而是左右描述的畸变矫正不一致! 经过查询相关资料,
这个不同点最终的影响不得而知,有谁知道的可以评论一下。
这个不同会导致一个问题,就是解畸变halcon和Opencv的过程是不一样的,halcon解畸变会更加简单,因为等号右边就是畸变的点,可以直接代入求解,但Opencv不是,它解畸变已知的是左边,求的是右边无畸变点,这个二元多次方程到底该怎么解呢?Opencv给出了一个解法。
Opencv解畸变
在 OpenCV 中,解畸变的函数主要包括 cv::undistort 和 cv::undistortPoints,我们这里看一下cv::undistortPoints函数,它里面最关键的是下面这段代码,两个for循环。
//遍历每个点
for( int i = 0; i < n; i++ )
{
double x, y, x0 = 0, y0 = 0, u, v;
u = x; v = y;
x = (x - cx)*ifx;
y = (y - cy)*ify;
if( _distCoeffs ) {
// compensate tilt distortion
cv::Vec3d vecUntilt = invMatTilt * cv::Vec3d(x, y, 1);
double invProj = vecUntilt(2) ? 1./vecUntilt(2) : 1;
x0 = x = invProj * vecUntilt(0);
y0 = y = invProj * vecUntilt(1);
double error = std::numeric_limits<double>::max();
// compensate distortion iteratively
//核心:迭代计算畸变点
for( int j = 0; ; j++ )
{
if ((criteria.type & cv::TermCriteria::COUNT) && j >= criteria.maxCount)
break;
if ((criteria.type & cv::TermCriteria::EPS) && error < criteria.epsilon)
break;
double r2 = x*x + y*y;
//下面这个是公式中的倒数
double icdist = (1 + ((k[7]*r2 + k[6])*r2 + k[5])*r2)/(1 + ((k[4]*r2 + k[1])*r2 + k[0])*r2);
if (icdist < 0) // test: undistortPoints.regression_14583
{
x = (u - cx)*ifx;
y = (v - cy)*ify;
break;
}
double deltaX = 2*k[2]*x*y + k[3]*(r2 + 2*x*x)+ k[8]*r2+k[9]*r2*r2;
double deltaY = k[2]*(r2 + 2*y*y) + 2*k[3]*x*y+ k[10]*r2+k[11]*r2*r2;
x = (x0 - deltaX)*icdist;
y = (y0 - deltaY)*icdist;
//解出来后再反向带回去,比较一下误差大小
if(criteria.type & cv::TermCriteria::EPS)
{
double r4, r6, a1, a2, a3, cdist, icdist2;
double xd, yd, xd0, yd0;
cv::Vec3d vecTilt;
r2 = x*x + y*y;
r4 = r2*r2;
r6 = r4*r2;
a1 = 2*x*y;
a2 = r2 + 2*x*x;
a3 = r2 + 2*y*y;
cdist = 1 + k[0]*r2 + k[1]*r4 + k[4]*r6;
icdist2 = 1./(1 + k[5]*r2 + k[6]*r4 + k[7]*r6);
xd0 = x*cdist*icdist2 + k[2]*a1 + k[3]*a2 + k[8]*r2+k[9]*r4;
yd0 = y*cdist*icdist2 + k[2]*a3 + k[3]*a1 + k[10]*r2+k[11]*r4;
vecTilt = matTilt*cv::Vec3d(xd0, yd0, 1);
invProj = vecTilt(2) ? 1./vecTilt(2) : 1;
xd = invProj * vecTilt(0);
yd = invProj * vecTilt(1);
double x_proj = xd*fx + cx;
double y_proj = yd*fy + cy;
error = sqrt( pow(x_proj - u, 2) + pow(y_proj - v, 2) );
}
}
}
关于这个公式,右边是无畸变的,现在已知的是左侧带畸变的
x
′
′
x^{”}
x′′,右边无畸变的
x
′
x^{‘}
x′看上去是不好求的。
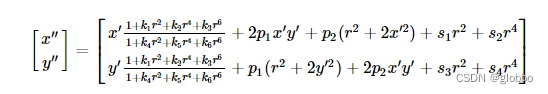
opencv使用的是不动点迭代求解非线性方程的根(参考https://blog.csdn.net/weixin_43956164/article/details/124197614),先在最里面的for中,将已知的带畸变的强行代入公式右边,注意设第一个
x
′
x^{‘}
x′是未知的,这样就变成了:
(
x
′
′
−
2
1
x
′
′
y
′
′
−
2
(
r
2
+
2
x
′
2
)
−
s
1
r
2
−
s
2
r
4
1
+
k
1
r
2
+
.
.
.
1
+
k
4
r
2
+
.
.
.
=
x
′
)
(frac{x^{”} – 2p_{1}x^{”}y^{”}-p_{2}(r^{2}+2x^{‘2}) – s_{1}r^{2} – s_{2}r^{4}}{frac{1+k_{1}r^{2}+…}{1+k_{4}r^{2}+…}}=x^{‘} )
(1+k4r2+…1+k1r2+…x′′−2p1x′′y′′−p2(r2+2x′2)−s1r2−s2r4=x′)
求出来的结果,再按
x
′
x^{‘}
x′和
y
′
y^{‘}
y′代入公式右侧,重新得到畸变的
x
′
′
x^{”}
x′′和
y
′
′
y^{”}
初始值设定对比
初始值的设定是很关键的,尤其在复杂的相机模型中比如沙姆模型。这里列一下opencv和张正友标定在初始值设置时的不同:
-
opencv
opencv可以通过传入标记CALIB_USE_INTRINSIC_GUESS来手动控制内参和畸变的初始参数,如果不设置该标记,那么opencv会通过cvInitIntrinsicParams2D计算内参中的焦距(其中的中心位置在该函数中强行设置为了图像中心!),然后根据内参调用cvFindExtrinsicCameraParams2来计算外参,这里全局一个内参矩阵,每个图像对应一个外参,具体的方法参考的张正友但又有不同。可以参考下面两个链接,讲的很详细:
https://blog.csdn.net/weixin_43956164/article/details/127408933
https://blog.csdn.net/weixin_43956164/article/details/126771627 -
总结
张正友内参是计算得出的,opencv可以传入初始内参,也可以进行估算,两个不同点在于:
a.opencv把中心点强行设为了图像坐标系中心,而zhang是放到内参中统一估算的;
b.opencv由于强行让内参的中心点设置为了已知量,所以化简的出了一个ax=b的矩阵,动用cvSolve去解得方程,而zhang更通用,中心点也是求出的,得出一个ax=0的矩阵方程,可以动用svd分解a矩阵,得到UWV,则V矩阵的最后一列即为ax=0的解。
原文地址:https://blog.csdn.net/hao1183716597/article/details/134331150
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。
如若转载,请注明出处:http://www.7code.cn/show_33254.html
如若内容造成侵权/违法违规/事实不符,请联系代码007邮箱:suwngjj01@126.com进行投诉反馈,一经查实,立即删除!







