1314. 矩阵区域和 – 力扣(LeetCode)
给你一个 m x n 的矩阵 mat 和一个整数 k ,请你返回一个矩阵 answer ,其中每个 answer[i][j] 是所有满足下述条件的元素 mat[r][c] 的和:
示例 1:
输入:mat = [[1,2,3],[4,5,6],[7,8,9]], k = 1
输出:[[12,21,16],[27,45,33],[24,39,28]]
示例 2:
输入:mat = [[1,2,3],[4,5,6],[7,8,9]], k = 2
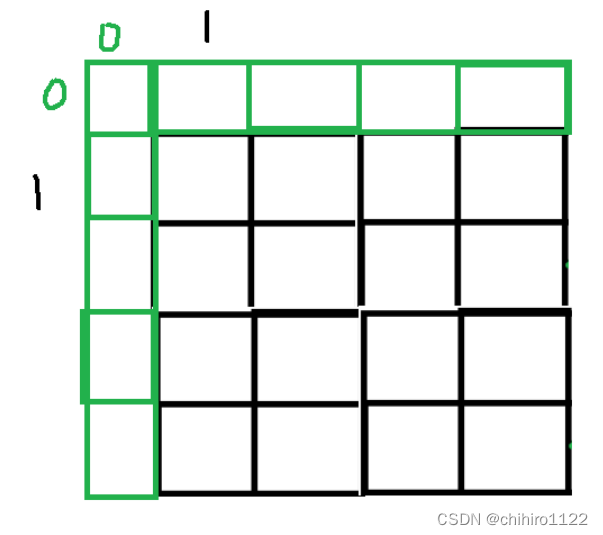
输出:[[45,45,45],[45,45,45],[45,45,45]]题意就是要计算 假设给出的 mat[i][j] ,那么就要是要计算下图当中给出的 区域的全部元素之和:
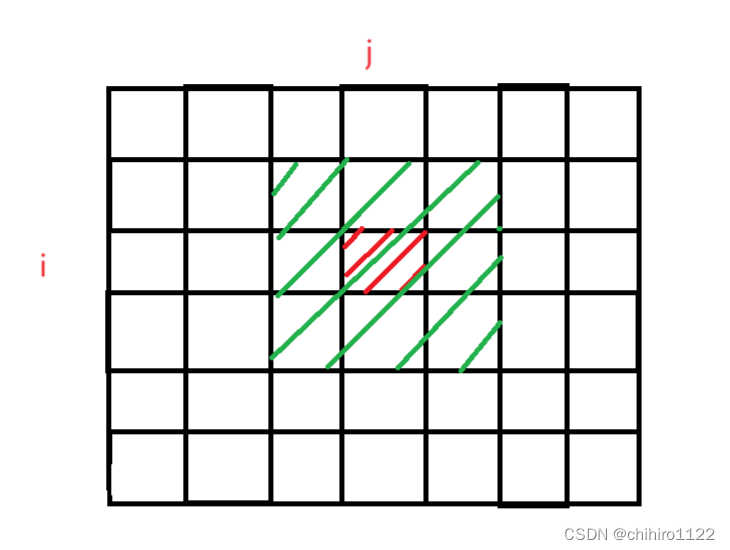
新返回的矩形当中,应该存储的是上述 绿色区域当中的全部的 元素之和。(k = 1)
leedcode 刷题 – 除自身以外数组的乘积 – 和为 K 的子数组-CSDN博客
leetcode – 串联所有单词的子串 – 最小覆盖子串 – x 的平方根-CSDN博客
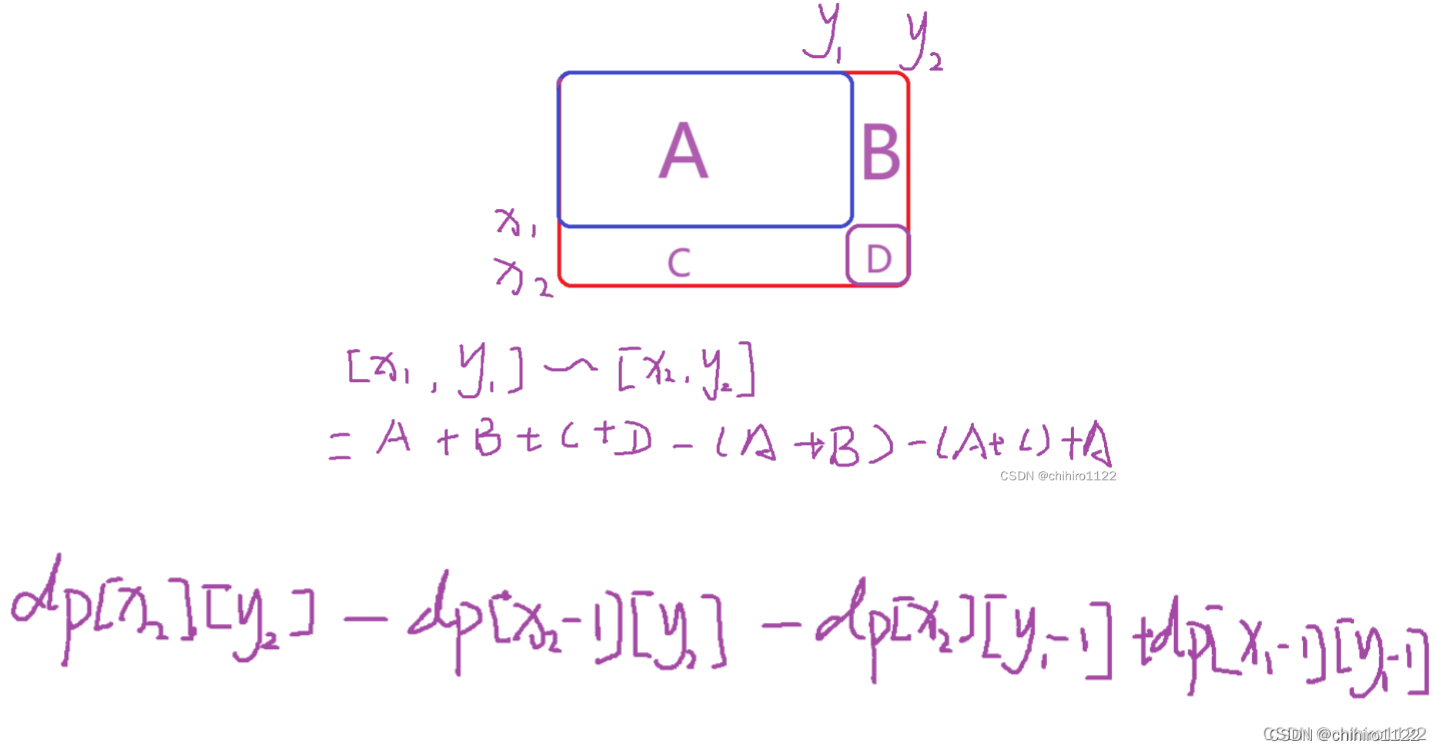
上述就是递归公式,但是 dp[x2][y2] 不是在 dp 这个 二维前缀和数组当中的,这个位置是没有 数据的,所以,其实这个位置的数据是在 mat 当中的。也就对应的是 mat[i][j] 。
所以,上述就计算出了存储前缀和的二维数组。
此时,我们只需要根据上述的 存储前缀和的二维数组,就可以像下图当中这样去 计算,某一个满足题意的 区间的 元素之和:

即:
ret = dp[x2][y2] - dp[x1 - 1][y2] - dp[x2][y1 - 1] + dp[x1 - 1][y1 - 1]上述就是递推公式。
在上述计算出递推公式之后,就可以开始计算上述的 x1 y1 和 x2 y2 了。
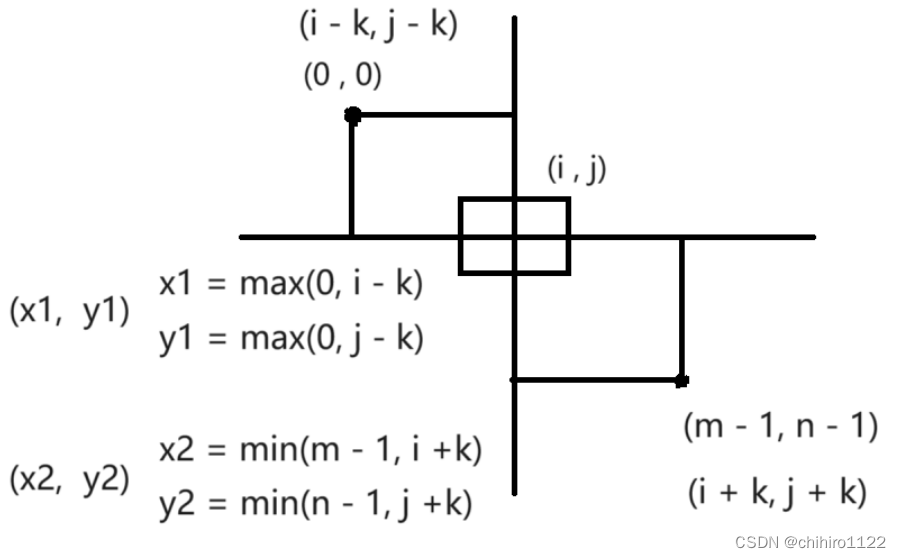
上述前缀和二维数组当中的 下标是从 (1, 1) 开始计数的,但是,在题目当中的二维数组是从 (0,0) 开始计数的,所以,为了方便上述 前缀和二维数组的计算,所以,我们直接把 dp 数组加一行加一列:
dp[x][y] -> mat[x - 1][y -1]
dp[x][y] -> ans[x - 1][y -1]所以此时应该是:
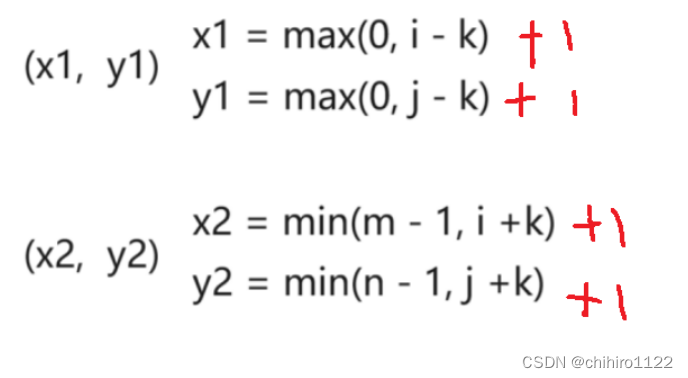
class Solution {
public:
vector<vector<int>> matrixBlockSum(vector<vector<int>>& mat, int k) {
int m = mat.size(), n = mat[0].size();
//计算出前缀和二维数组
vector<vector<int>> dp(m + 1, vector<int>(n + 1));
for(int i = 1;i <= m;i++)
for(int j = 1;j <= n;j++)
dp[i][j] = dp[i - 1][j] + dp[i][j - 1] - dp[i - 1][j - 1] + mat[i - 1][j - 1];
// 计算出 answer 二维数组的值
vector<vector<int>> ret(m, vector<int>(n));
for(int i = 0;i < m;i++)
for(int j = 0;j < n;j++)
{
int x1 = max(0 , i - k) + 1, y1 = max(0 , j - k) + 1;
int x2 = min(m - 1 , i + k) + 1, y2 = min(n - 1 , j + k) + 1;
ret[i][j] = dp[x2][y2] - dp[x1 - 1][y2] - dp[x2][y1 - 1] + dp[x1 - 1][y1 - 1];
}
return ret;
}
};原文地址:https://blog.csdn.net/chihiro1122/article/details/134637097
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。
如若转载,请注明出处:http://www.7code.cn/show_34528.html
如若内容造成侵权/违法违规/事实不符,请联系代码007邮箱:suwngjj01@126.com进行投诉反馈,一经查实,立即删除!