彻底明白回溯算法【三个例子】

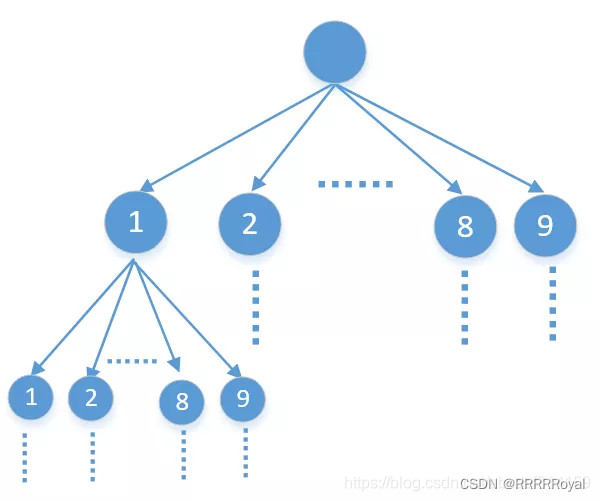
回溯算法可以理解为一种通过试错的方式来达到问题的解决。在解决问题过程中，当它通过尝试发现现有的解决方案不行时，它会取消上一步甚至是上几步的计算，再通过其他的可能的分步解决方案继续尝试寻找问题的答案。回溯算法非常适合用来解决由多个步骤组成的问题，其中每个步骤都有多个选项。当我们在某一步选择了其中一个选项时，就进入到了下一步，然后面临新的选择。我们就这样重复选择和进入下一步的过程，如果发现某一步的选择无论如何都无法达到最终的要求，就退回到上一步，重新选择，这样反复进行，直到找到可能的解决方案或所有的选项都试过，但没有办法得到满意的解决方案。

回溯算法通常用递归的方式实现，递归是函数自己调用自己的一种方式，使用递归可以使问题的解决方案更加简洁明了。在编程实现中，回溯算法可以被划分为三个主要的部分：

1. 路径：它记录了从起点到当前点的路径。
2. 选择列表：它记录了你当前可以做的选择。
3. 结束条件：它判断当前的路径是否满足题目的要求，并结束递归。

接下来，我会通过三个经典回溯算法问题来详细说明这个算法的实现。

经典问题一：N皇后问题

问题描述：

在一个N×N的棋盘上放置N个皇后，需要满足皇后之间互不攻击的条件（即任意两个皇后不能处在同一行、同一列以及同一斜线上）。求解所有可能的配置方式。

解题思路：

• 路径：采用一个数组来表示棋盘上皇后的摆放位置。数组的下标表示皇后所在的行，数组元素的值表示皇后所在的列。例如，queens[i]=j表示第i行的皇后放在第j列。
• 选择列表：对于每一行，都需要选择一个不冲突的列位置。可以定义一个函数，这个函数检查当前列和斜线上是否已经有皇后存在。
• 结束条件：所有的行都成功放置了皇后。

下面是C++实现的代码示例，代码中将包含详细的中文注释：

#include <iostream>
#include <vector>
#include <string>

using namespace std;

// 检查当前放置的皇后和之前的皇后是否冲突
bool isSafe(int row, int col, vector<int&gt; &amp;position) {
    for (int i = 0; i < row; ++i) {
        // 检查列冲突和对角线冲突
        if (position[i] == col || abs(row - i) == abs(col - position[i])) {
            return false;
        }
    }
    return true;
}

// 回溯函数，尝试在棋盘的每一行放置皇后
void placeQueens(int row, int n, vector<int&gt; &amp;position, vector<vector<string&gt;&gt; &amp;solutions) {
    if (row == n) { // 所有的皇后都放置好了，转换为输出格式
        vector<string> board(n, string(n, '.'));
        for (int i = 0; i < n; ++i) {
            board[i][position[i]] = 'Q';
        }
        solutions.push_back(board);
    } else {
        for (int col = 0; col < n; ++col) { // 遍历当前行的每一列
            if (isSafe(row, col, position)) { // 判断是否可以放置皇后
                position[row] = col; // 放置皇后
                placeQueens(row + 1, n, position, solutions); // 递归放置下一行的皇后
                // 回溯部分，撤销当前行的皇后放置
            }
        }
    }
}

vector<vector<string>> solveNQueens(int n) {
    vector<vector<string>> solutions; // 存储所有解决方案
    vector<int> position(n); // 每行皇后的放置位置
    placeQueens(0, n, position, solutions); // 从第一行开始放置皇后
    return solutions;
}

int main() {
    int n = 8; // 可以改变这个值来求解不同大小的棋盘
    vector<vector<string>> solutions = solveNQueens(n);
    cout << "There are " << solutions.size() << " solutions to the " << n << "-Queens problem." << endl;
    for (auto &amp;solution : solutions) {
        for (auto &amp;row : solution) {
            cout << row << endl;
        }
        cout << endl;
    }
    return 0;
}

在上面的代码中，我们首先定义了一个辅助函数isSafe，它用于检查在当前行的某一列放置皇后是否会发生冲突。然后，placeQueens函数用于递归尝试在棋盘上放置皇后，它首先会检查整个棋盘是否已经放满皇后，如果已经放满了，就会生成一个解决方案并添加到solutions列表中。在放置皇后时，如果在某一列上放置皇后不发生冲突，那么就在那一列放置皇后，并递归地放置下一行的皇后。一旦发现这一列不能放置皇后，或者放置了皇后之后，下一行没有合适的位置可以放置皇后，就会进行回溯，撤销当前的放置并尝试下一列。

经典问题二：全排列问题

问题描述：

给定一个不含重复数字的数组，返回其所有可能的全排列。

解题思路：

• 路径：记录一个排列中已经选择过的数字。
• 选择列表：记录当前可以选择的数字。
• 结束条件：当排列长度等于输入数组的长度时，说明一个完整的排列已经构建完成。

#include <iostream>
#include <vector>
using namespace std;

void backtrack(vector<int> &amp;nums, vector<vector<int>> &amp;res, vector<int> &amp;track, vector<bool> &amp;used) {
    // 结束条件：路径长度等于数组长度，说明已经完成了一次排列
    if (track.size() == nums.size()) {
        res.push_back(track);
        return;
    }
    for (int i = 0; i < nums.size(); i++) {
        // 排除不正确的选择，如果数字已经在路径中，则不能再被选择
        if (used[i]) continue;
        // 做选择
        track.push_back(nums[i]);
        used[i] = true;
        // 进入下一层决策树
        backtrack(nums, res, track, used);
        // 取消选择
        track.pop_back();
        used[i] = false;
    }
}

vector<vector<int>> permute(vector<int>&amp; nums) {
    vector<vector<int>> res;
    vector<int> track; // 路径，记录在 track 中的排列顺序
    vector<bool> used(nums.size(), false); // 使用一个数组标记元素是否在路径中被使用
    backtrack(nums, res, track, used); // 调用回溯函数
    return res; // 返回结果
}

int main() {
    vector<int> nums = {1,2,3};
    vector<vector<int>> res = permute(nums);
    for (auto &amp;perm : res) {
        for (int num : perm) {
            cout << num << " ";
        }
        cout << endl;
    }
    return 0;
}

以上代码首先定义了backtrack函数，用来进行回溯搜索排列。在搜索过程中，我们用一个track数组来记录当前的选择路径，用一个used数组来标记数组中的元素是否被使用过。当track数组的大小等于输入数组nums的大小时，说明已经得到了一个完整的排列，将其添加到结果列表res中。在每一次尝试选择数组中的一个数字放入路径时，需要检查这个数字之前是否已经被使用过了，如果已经使用过，则跳过，反之则加入到路径中，并标记为已使用，然后递归地进行下一次选择。当一次递归返回时，取消当前的选择，继续尝试其他的数字。

经典问题三：组合总和问题

问题描述：

给定一个无重复元素的数组和一个目标数 target，找出数组中所有可以使数字和为 target 的组合。数组中的数字可以无限制重复被选取。

解题思路：

• 路径：记录当前的组合路径，即哪些数字被选取了。
• 选择列表：表示当前可以选择的数字，由于可以重复选择，所以选择列表始终是原数组。
• 结束条件：当路径中的数字和等于 target 时，将当前组合放入结果列表中；如果和大于 target，结束当前路径的搜索。

#include <iostream>
#include <vector>
using namespace std;

// 回溯
void backtrack(vector<int>&amp; candidates, int target, vector<int>&amp; track, int start, vector<vector<int>>&amp; res) {
    // 如果路径上数字和已经大于 target，结束递归
    if (target < 0) {
        return;
    }
    // 当组合中数字和等于 target，将它加入结果集中
    if (target == 0) {
        res.push_back(track);
        return;
    }
    // 从 start 开始防止产生重复的组合
    for (int i = start; i < candidates.size(); i++) {
        // 选择当前数字
        track.push_back(candidates[i]);
        // 由于数字可以重复选择，下一轮还从 i 开始
        backtrack(candidates, target - candidates[i], track, i, res);
        // 撤销选择
        track.pop_back();
    }
}

vector<vector<int>> combinationSum(vector<int>&amp; candidates, int target) {
    vector<vector<int>> res;
    vector<int> track;
    backtrack(candidates, target, track, 0, res);
    return res;
}

int main() {
    vector<int> candidates = {2,3,6,7};
    int target = 7;
    vector<vector<int>> res = combinationSum(candidates, target);
    for (const auto &comb : res) {
        for (int num : comb) {
            cout << num << " ";
        }
        cout << endl;
    }
    return 0;
}

在上述代码中，backtrack函数采用了额外的变量start来防止产生重复的组合。我们将所有可能的数字组合搜索一遍，如果当前路径上数字的和大于目标数target，我们就停止递归；如果和等于目标数，则将这个组合保存到结果列表中。与全排列的问题不同，由于每个数字可以被无限次选择，我们在下一个递归调用仍然从当前位置开始。

以上介绍的三个问题都是回溯算法问题的典型代表。通过这些例子，可以看出回溯算法是一种框架通用的算法，适用于多种问题的求解。它通过在问题的解空间树中，利用深度优先搜索的策略，尝试每一种可能的解法。如果当前走的路径最终不可能到达正确答案，算法就会返回，尝试其他的路径，这就是所谓的“回溯”。尽管回溯算法在最坏情况下的时间复杂度比较高，但通过适当的剪枝优化，通常可以大幅度提高算法的效率，使其成为解决许多组合问题的有力工具。

如果你想更深入地了解人工智能的其他方面，比如机器学习、深度学习、自然语言处理等等，也可以点击这个链接，我按照如下图所示的学习路线为大家整理了100多G的学习资源，基本涵盖了人工智能学习的所有内容，包括了目前人工智能领域最新顶会论文合集和丰富详细的项目实战资料，可以帮助你入门和进阶。

链接： 人工智能交流群【最新顶会与项目实战】（点击跳转）

代码007普通

打赏 收藏 海报 链接