使用向量化的方法会使得计算更为简便。以上面的神经网络为例,试着计算第二层的值:

我们令
z
(
2
)
=
θ
(
1
)
{{z}^{left( 2 right)}}={{theta }^{left( 1 right)}}x
z(2)=θ(1)x,则
(
2
)
=
(
z
(
2
)
)
{{a}^{left( 2 right)}}=g({{z}^{left( 2 right)}})
a
0
(
2
)
=
1
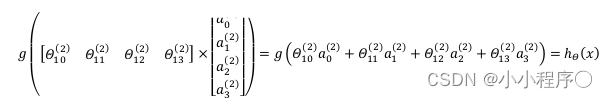
我们令
z
(
3
)
=
θ
(
2
)
a
(
2
)
{{z}^{left( 3 right)}}={{theta }^{left( 2 right)}}{{a}^{left( 2 right)}}
z(3)=θ(2)a(2),则
θ
(
x
)
=
a
(
3
)
=
(
z
(
3
)
)
h_theta(x)={{a}^{left( 3 right)}}=g({{z}^{left( 3 right)}})
hθ(x)=a(3)=g(z(3))。
这只是针对训练集中一个训练实例所进行的计算。如果我们要对整个训练集进行计算,我们需要将训练集特征矩阵进行转置,使得同一个实例的特征都在同一列里。即:
${{z}^{left( 2 right)}}={{Theta }^{left( 1 right)}}times {{X}^{T}} $
a
(
2
)
=
g
(
z
(
2
)
)
{{a}^{left( 2 right)}}=g({{z}^{left( 2 right)}})
a(2)=g(z(2))
为了更好了了解Neuron Networks的工作原理,我们先把左半部分遮住:

a
0
,
a
1
,
a
2
,
a
3
a_0, a_1, a_2, a_3
a0,a1,a2,a3, 按照Logistic Regression的方式输出
h
θ
(
x
)
h_theta(x)
hθ(x)
其实神经网络就像是logistic regression,只不过我们把logistic regression中的输入向量
[
x
1
∼
x
3
]
[x1∼x3] 变成了中间层的
[
a
1
(
2
)
∼
a
3
(
2
)
]
left[ a_1^{(2)}sim a_3^{(2)} right]
[a1(2)∼a3(2)], 即:
h
θ
(
x
)
=
g
(
Θ
0
(
2
)
a
0
(
2
)
+
Θ
1
(
2
)
a
1
(
2
)
+
Θ
2
(
2
)
a
2
(
2
)
+
Θ
3
(
2
)
a
3
(
2
)
)
h_theta(x)=gleft( Theta_0^{left( 2 right)}a_0^{left( 2 right)}+Theta_1^{left( 2 right)}a_1^{left( 2 right)}+Theta_{2}^{left( 2 right)}a_{2}^{left( 2 right)}+Theta_{3}^{left( 2 right)}a_{3}^{left( 2 right)} right)
hθ(x)=g(Θ0(2)a0(2)+Θ1(2)a1(2)+Θ2(2)a2(2)+Θ3(2)a3(2))
我们可以把
a
0
,
a
1
,
a
2
,
a
3
a_0, a_1, a_2, a_3
x
0
,
x
1
,
x
2
,
x
3
x_0, x_1, x_2, x_3
x0,x1,x2,x3的进化体,并且它们是由
x
x
x与
θ
θ决定的,因为是梯度下降的,所以
a
a
a是变化的,并且变得越来越厉害,所以这些更高级的特征值远比仅仅将
x
x
x次方厉害,也能更好的预测新数据。
这就是神经网络相比于逻辑回归和线性回归的优势。
原文地址:https://blog.csdn.net/2201_75381449/article/details/134757985
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。
如若转载,请注明出处:http://www.7code.cn/show_35206.html
如若内容造成侵权/违法违规/事实不符,请联系代码007邮箱:suwngjj01@126.com进行投诉反馈,一经查实,立即删除!