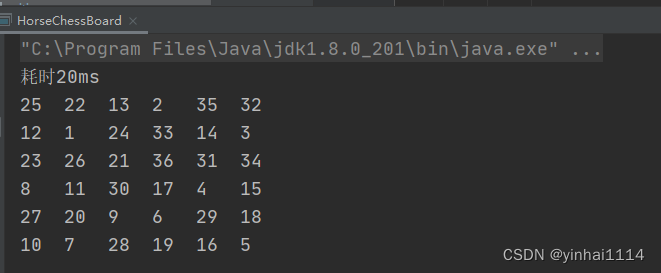
本文介绍: 1.马踏棋盘问题(骑士周游问题)实际上是图的深度优先搜索(DFS)的应用。2.如果使用回溯(就是深度优先搜索)来解决,假如马儿踏了53个点,如图:走到了第53个,坐标(1,0),发现已经走到尽头,没办法,那就只能回退了,查看其他的路径,就在棋盘上不停的….. ,思路分析+代码实现3.先用基本方式来解决,然后使用贪心算法(greedyalgorithm) 进行优化。解决马踏棋盘问题,体会到不同的算法对程序效率的影响4.使用前面的游戏来验证算法是否正确。
一、意义
1.算法是程序的灵魂,为什么有些程序可以在海量数据计算时,依然保持高速计算?
2.拿老韩实际工作经历来说,在Unix下开发服务器程序,功能是要支持上千万人同时在线,在上线前, 做内测,一切OK,可上线后,服务器就支撑不住了,公司的CTO对代码进行优化,再次上线,坚如磐石。那一瞬间,你就能感受到程序是有灵魂的,就是算法。
3.编程中算法很多,比如八大排序算法(冒泡、选择、插入、快排、归并、希尔、基数、堆排序、查找算法、分治算法、动态规划算法、KMP算法、贪心算法、普里姆算法、克鲁斯卡尔算法、迪杰斯特拉算法、弗洛伊德算法
4.老韩以骑士周游问题为例,让小伙伴体验用算法去优化程序的意义,让大家直观的感受到算法的威力
二、经典算法问题 – 骑士周游问题
2.将马随机放在国际象棋的8x 8棋盘Board[0 ~ 7][0 ~ 7]的某个方格中,马按走棋规则(马走日字)进行移动。要求每个方格只进入次,走遍棋盘上全部64个方格
算法介绍
解决步骤和思路分析
对代码使用贪心算法,进行优化,提高速度
声明:本站所有文章,如无特殊说明或标注,均为本站原创发布。任何个人或组织,在未征得本站同意时,禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益,可联系我们进行处理。