本文介绍: talib 的Statistic Functions 统计指标函数,包括BETA ,CORREL ,LINEARREG,LINEARREG_ANGLE ,LINEARREG_INTERCEPT,LINEARREG_SLOPE,STDDEV ,TSF,VAR ,使用示例和图示。
TA-Lib学习研究笔记——Statistic Functions (六)
1.BETA – Beta
函数名:BETA
名称:β系数也称为贝塔系数
简介:一种风险指数,用来衡量个别股票或股票基金相对于整个股市的价格波动情况贝塔系数衡量股票收益相对于业绩评价基准收益的总体波动性,是一个相对指标。 β 越高,意味着股票相对于业绩评价基准的波动性越大。 β 大于 1 ,则股票的波动性大于业绩评价基准的波动性。反之亦然。
用途:
1)计算资本成本,做出投资决策(只有回报率高于资本成本的项目才应投资);
2)计算资本成本,制定业绩考核及激励标准;
3)计算资本成本,进行资产估值(Beta是现金流贴现模型的基础);
4)确定单个资产或组合的系统风险,用于资产组合的投资管理,特别是股指期货或其他金融衍生品的避险(或投机)
语法:
说明:
df_index是深证指数,由于数据级别差异大,分别做图。
也可以用成交金额对比,amount 。
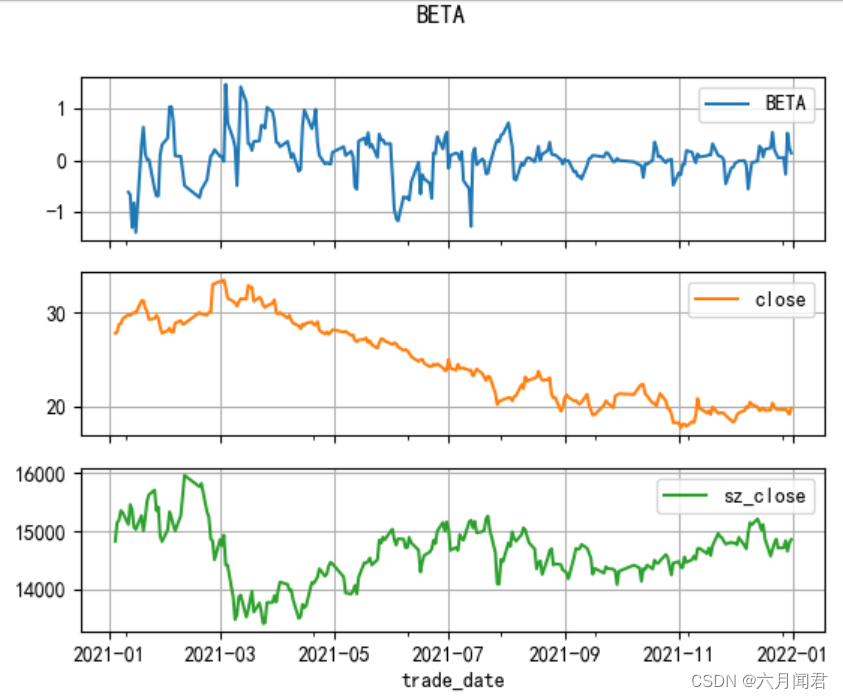
用amount做测试一下,数据差别大,通过标准化数据,进行对比分析:
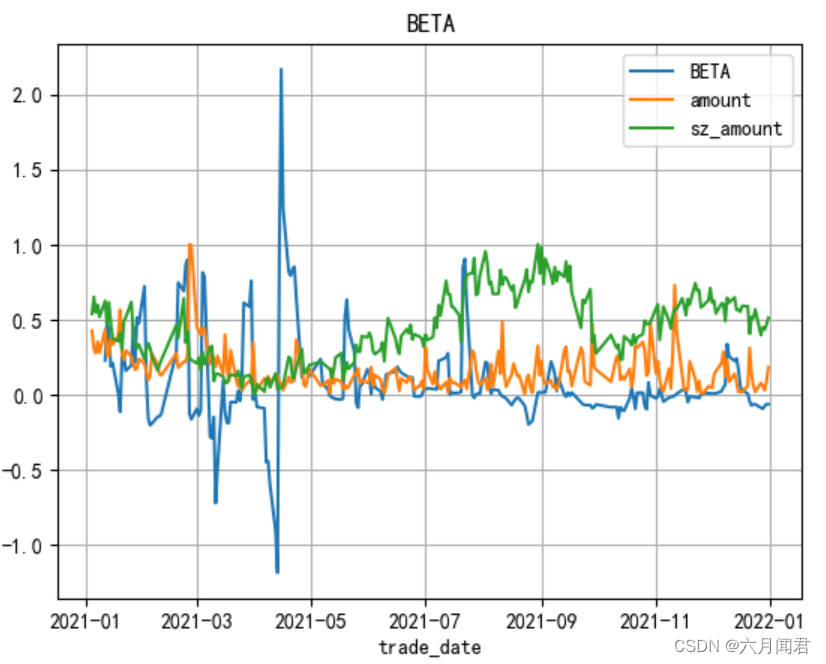
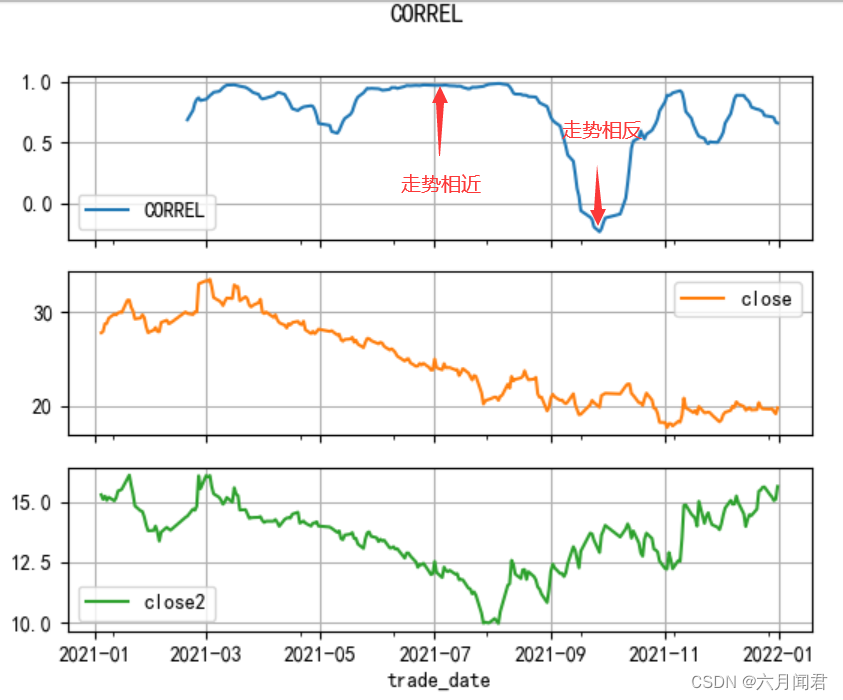
2.CORREL
Pearson’s Correlation Coefficient ®
函数名:CORREL
名称:皮尔逊相关系数
简介:用于度量两个变量X和Y之间的相关(线性相关),其值介于-1与1之间皮尔逊相关系数是一种度量两个变量间相关程度的方法。它是一个介于 1 和 -1 之间的值,其中,1 表示变量完全正相关, 0 表示无关,-1 表示完全负相关。
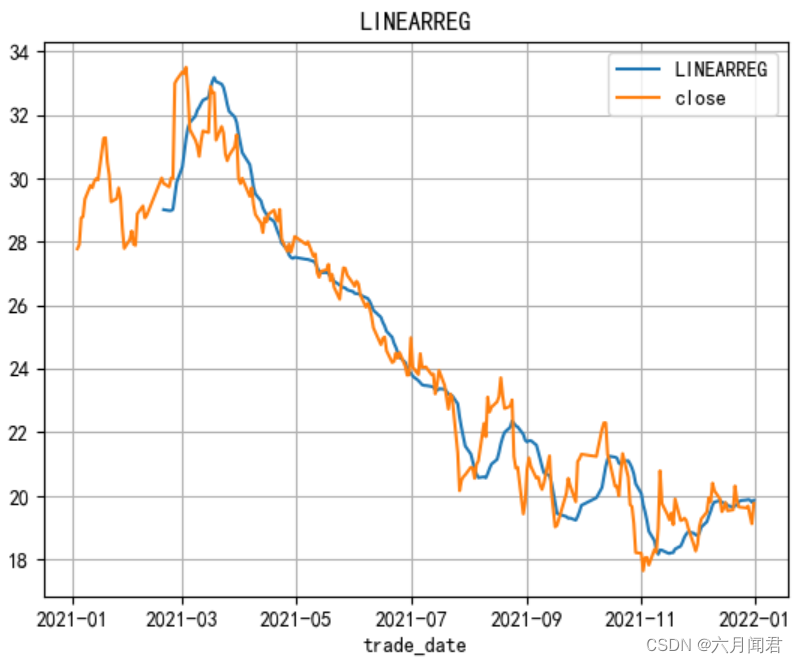
3.LINEARREG
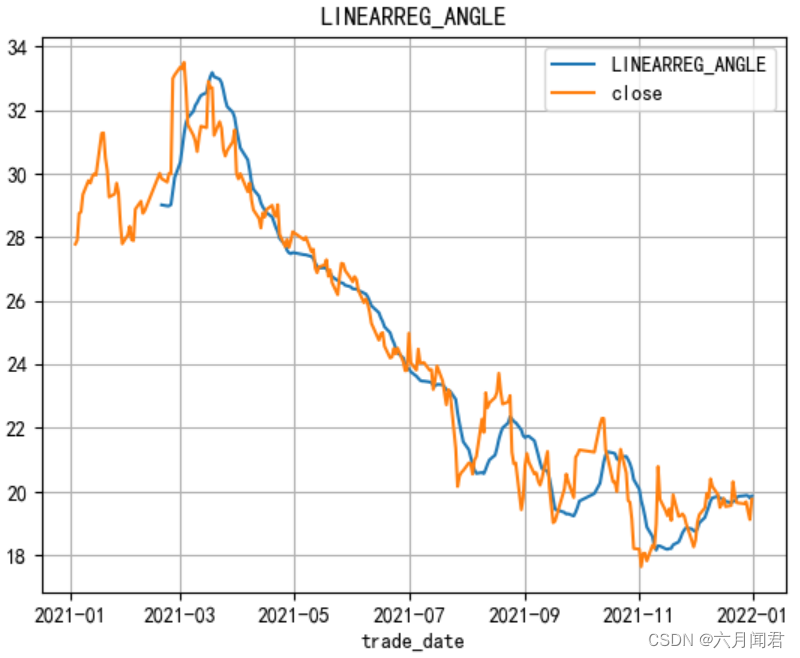
4.LINEARREG_ANGLE
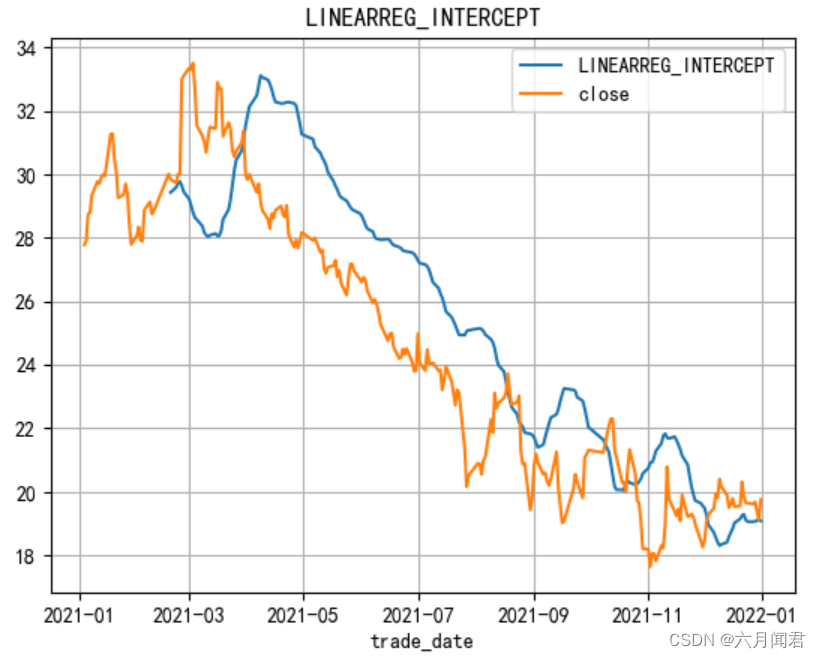
5.LINEARREG_INTERCEPT
6.LINEARREG_SLOPE
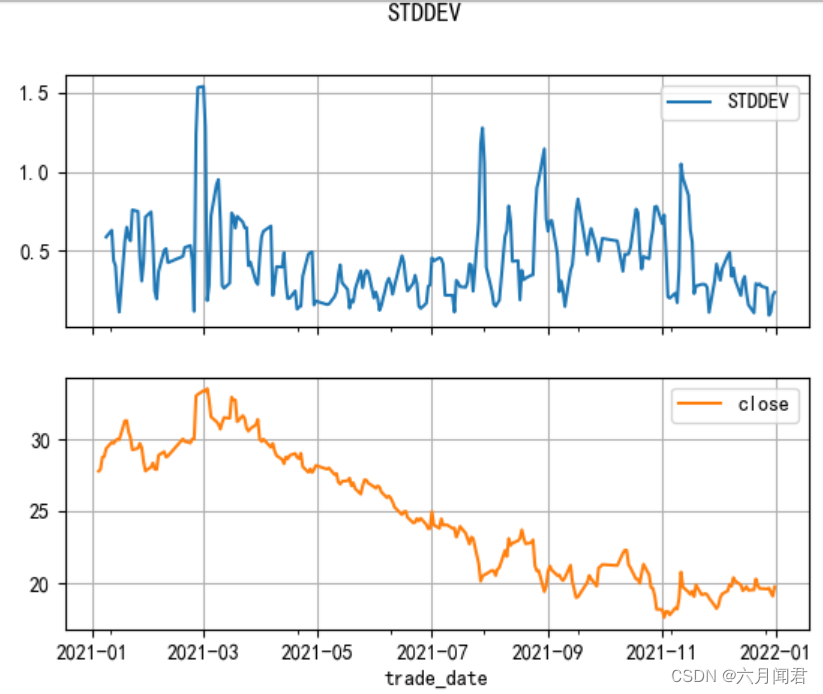
7.STDDEV
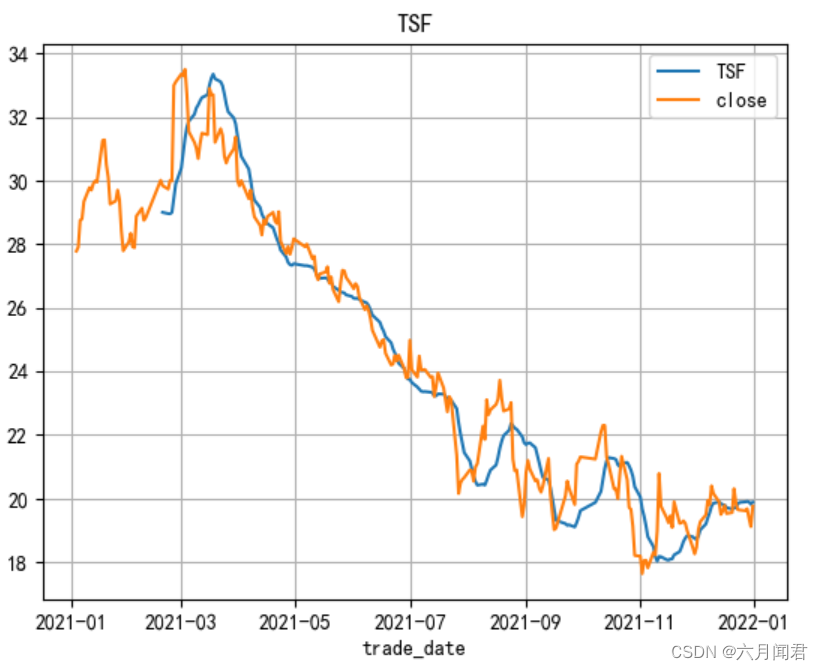
8.TSF
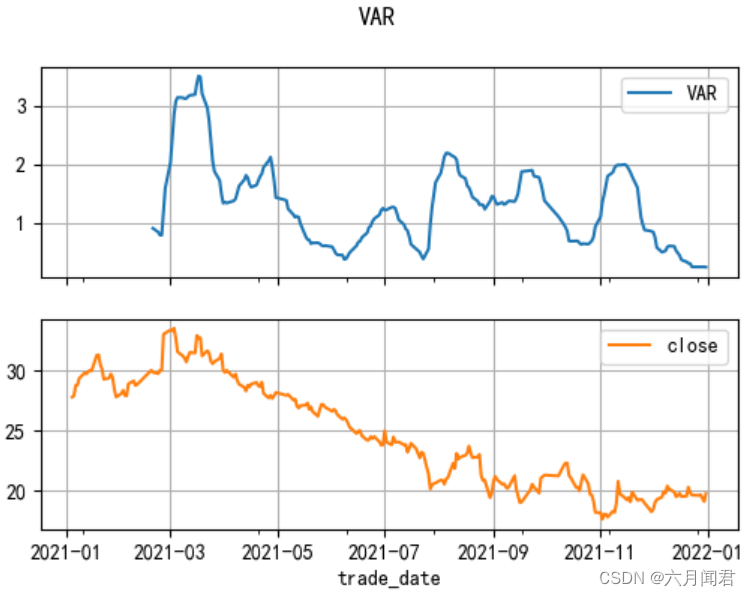
9.VAR
声明:本站所有文章,如无特殊说明或标注,均为本站原创发布。任何个人或组织,在未征得本站同意时,禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益,可联系我们进行处理。