7. 空间分析
地理信息系统(GIS)与计算机辅助绘图系统(CAD)的主要区别是GIS提供了对原始空间数据实施转换以回答特定查询的能力,而这些变换能力中最核心的部分就是对空间数据的利用和分析,即空间分析能力。可以认为空间分析是GIS中最为重要的内容之一,体现了GIS的本质。
7.1 空间分析的内容与步骤
通过开发和应用适当的数据模型,用户可以使用GIS的空间分析功能来研究现实世界。由于模型中蕴涵着空间数据的潜在趋向,从而可能由此得到新的信息。GIS提供一系列的空间分析工具,用户可以将它们组合成一个操作序列,从已有模型来求得一个新模型,而这个新模型就可能展现出数据集内部或数据集之间新的或未曾明确的关系,从而深化我们对现实世界的理解。
1.拓扑分析 包括空间图形数据的拓扑运算,即旋转变换、比例尺变换、三维及三维显示、几何元素计算等。
2.属性分析 包括数据检索、逻辑与数学运算、重分类、统计分析等。
3.拓扑与属性的联合分析 包括与拓扑相关的数据检索、叠置处理、区域分析、邻域分析、网络分析、形状探测、瘦化处理、空间内插等。
由此可见,空间分析的内容相当宽泛。在本章中,我们只限于讨论数据检索及表格分析、多边形叠置、缓冲分析、网络分析等若干核心内容,其它方面的内容或分散于其余章节,或单独成章讨论。
在实施空间分析之前,需要对问题进行评估并建立目标。在对数据作任何判断或得出任何结论之前,要全面考虑处理过程;要对数据和模型提出充分的问题;要制订明确的步骤来勾画全面的目标并控制进展。
空间分析大致有以下步骤:
1.建立分析的目的和标准
分析的目的定义了你打算利用地理数据库回答什么问题,而标准则具体规定了你将如何利用GIS回答你所提出的问题。例如,某项研究的目的可能是确定适合建造一个新的公园的位置,或者是计算由于洪水可能造成的损失。而满足这些目的的标准应该表述成一系列空间询问,这样才有利于分析。例如,下面列出了一些可能用于公园选址的标准:
(1)公园的位置既要交通便利又要环境安静,也就是说距主要公路的距离要适当。
(3)使公园的可利用面积最大,公园中应很少或没有沿河流分布的沼泽地。
上述各个标准可以利用缓冲分析、线段与多边形的叠加等空间操作(详见以下各节)来分析,在完成这些空间操作之后,你可以对适合于建造新公园的不同土地区域作出评价。
数据准备在信息系统的建立过程中是一个非常重要的阶段,在这个阶段,GIS用户需要做大量耐心细致的工作,需要投入大量的资金和人力来建立地理数据库。
在做空间分析之前,地理数据库还可能要作一些修改,如转换单位、略去数据库中的某些部分等。这个阶段往往要生成新的属性数据库或在原有数据库中增加新的属性项。
对于数据准备的要求随研究对象而异。在进行分析之前,对数据准备进行全面的考虑,将有助于更有效地完成工作。
3.进行空间分析操作
为了得到所需数据,可能需要进行许多操作(检索提取、缓冲、叠置等),每一步的空间操作都用来满足步骤一中所提出的一项标准。
4.准备表格分析的数据
大多数分析都要求利用空间操作得到一个(或一组)最终的数据层,然后就必须准备用于分析的数据,包括空间和属性数据。
所生成的层的属性表包括了利用逻辑表达式和算术表达式进行表格分析的信息。通常必须将进行分析时所需要的数据项加到属性表中。例如,你想根据地块数据层中的地块面积、现有结构和土壤类型来计算地块财产值,那么就要在属性表中加入一个数据项(取名可能是“VALUE”)来存放财产值。
5.进行表格分析
利用逻辑表达式和算术表达式,可以对在步骤三中进行的空间操作所获得的新的属性关系进行分析。在本步骤中,将利用步骤一中所确定的标准,定义一系列逻辑运算和算术运算,来对所得到的地理数据库进行操作。
当你通过表格分析获得了一个答案,你就必须对结果进行评价,以确定其有效性,该结果是否提供了可靠而又有意义的答案?这是一个重要的验证步骤,必要时可能还需要请一些有关专家来帮助你解译和验证结果。
7.如有必要,改进分析
如果感到你的分析还有局限性和缺点,你可以进一步改善,返回适当的步骤重新分析。
空间分析的成果往往表现为图件或报表。图件对于凸显地理关系是最好不过的,而报表则用于概括表格数据并记录计算结果。
理想状况下,空间分析功能应该独立于数据模型,例如缓冲(Buffer)操作并不取决于矢量或栅格系统的选择,用户不需了解特殊的技术细节。当然,从系统实现的角度来看,基于矢量方式的分析和基于栅格方式的分析是不大一样的。在对诸如面积等几何元素实施计算时,矢量方式是根据研究对象的坐标数据,而栅格方式则是对像元进行计数。与栅格方式相比,矢量方式下的某些操作更精确(如基于多边形的面积量算比栅格中的像元计数要精确,计算多边形周长也比统计区域边界的像元的边缘要精确),某些操作更快(如沿道路网络查找路径),但某些操作则更为复杂或慢得多(如多层叠置、缓冲区查找等)。
7.2 数据检索及表格分析
数据检索及表格分析可能只是单纯地针对属性数据(“全部区域的人口总和是多少?”),也可能是单纯依据空间拓扑关系(“河北省与那些省份相邻?”),但更多、更有意义的情况是将空间数据与属性联合起来实施检索分析(“某图斑周边有哪些地类为水浇地的图斑?”),换言之,检索条件可以是属性、空间拓扑限制或者是前二者的结合。检索分析的结果可能只是向用户提供一个统计结果;或者是将结果作为一个新的属性域添加到属性数据库中,还可能生成一个新的数据层。
7.2.1 属性统计分析
单纯对属性数据库的统计分析包括单属性统计、单属性函数变换、双属性分类统计、双属性数学运算等等。
单属性统计是对属性数据库中的某个字段,统计总和、最大值、最小值及平均值,给出字段值落在各个区间内或等于各个离散值的记录数,并据此绘制各类统计图(折线、直方、立体直方、饼图、立体饼图等)。这一功能在GIS中的使用是相当频繁的。如城市管网系统中,用户常常提出诸如“管网总长是多少?”、“管径大于300的管段有多少?”、“各类材质的管段分别有多少?”等问题,这些都可以通过单属性统计来获得答案。
单属性函数变换是对选定的初等函数,将属性字段作为函数自变量,将字段值依次带入初等函数,得到变换结果。系统常常是让用户在属性数据库中选择一个已有字段或在属性数据库中扩充一个字段来存放运算结果。用来作计算的函数可以有很多,如幂函数、指数函数、对数函数、三角函数、反三角函数等等。很多函数对变量域有限制(如对数函数中真值要大于零),系统应允许指定缺省值,当变量非法时将结果设置为此缺省值。
双属性分类统计除了要选择分类字段,并划分出各类范围外,还需要指定统计字段和统计方式。统计方式分计数方式和累计方式,其中计数方式是累计各类图元数,而累计方式则是将每一类的累计字段值相加。
以土地详查为例,假定现有某一数据层是一个县的全部图斑(区数据),图斑属性中有权属号(记录图斑所属县、乡、村)、面积、地类等字段,现要统计各村图斑总面积,就可以将图斑属性中的“权属号”作为分类字段,“面积”作为统计字段,统计方式是累计方式;如果要统计各村每类用地的数目,则要将“地类”作为统计字段,采用计数方式来统计。
7.2.2 布尔逻辑查询
使用布尔逻辑的规则对属性以及空间特性进行运算操作来检索数据使GIS在检索功能方面具有了极大的灵活性,因为它允许用户按属性数据、空间特性形成任意的组合条件来查询数据。布尔逻辑的运算有和(AND)、或(OR)、异或(XOR)、非(NOT)等。
例如,在地下管网信息系统中假设集合A是埋深小于三米的煤气管道,集合B是长度大于300米的煤气管道。那么,逻辑运算A AND B 就检索出埋深小于3米且长度大于300米的所有煤气管;A OR B 则检索出埋深小于3米及长度大于300米的所有煤气管;A XOR B检索出所有埋深小于3米及长度大于300米的所有煤气管,但不包括两条件同时满足的那些:A AND NOT B 则检索出埋深小于3米但长度小于或等于300米的所有煤气管。
7.2.3 空间数据库查询语言
不同系统使用不同的查询方式,这就导致应用上的很多麻烦,因此人们一直在寻找适用于GIS的通用查询语言,并致力于建立相应标准。
GIS中的查询首先是数据库的查询, SQL(Structured Query Language )作为关系型数据库的标准查询语言,因为它的非过程化描述和简洁性而备受青睐,为许多GIS所采用。
SELECT <属性名> FROM <属性表> WHERE <条件>
空间数据库是一种特殊的数据库,它与普通数据库的最大不同在于包含空间概念,而标准SQL语言不支持空间概念,目前多数GIS系统对此的解决方案是在SQL的基础上扩展空间概念描述、空间函数或空间操作,如增加WITHIN算子(SELECT <目标> WITHIN <区域>),但目前的效果尚不太理想。
也有一些实验性的GIS系统使用自然语言(受限的)来作为查询接口,虽然存在很大困难,这种方式仍是很有吸引力和应用前景的。
7.2.4 重分类,边界消除与合并
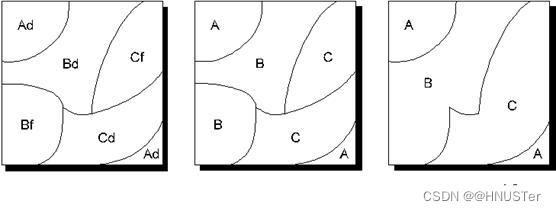
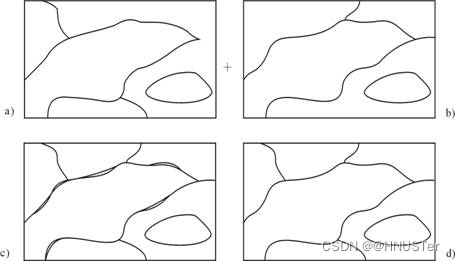
重分类、边界消除与合并(Reclassify, dissolve and merge)常常用在区域(多边形)数据的操作中。它们用来根据属性聚合区域。下图是一个例子。我们希望从一个数据层中得到土壤类型分布图,原始数据层中的多边形是根据更细的类别来划分的(每一个多边形中土壤类型和植被类型完全一致,见图(a))。
(用大写字母表示土壤类型的分类,小写字母表示植被类型的分类)
为了达到目的,我们实施以下步骤:
1. 按照土壤类型这个属性项对原始数据层重分类。见图(b)。
2.如果两相邻多边形具有相同土壤类型,则删除它们间的分界弧段,这就是边界消除。
3. 重建拓扑,将没有分界弧段的相邻多边形合成一个。见图(c)。
7.3 叠置分析
叠置分析是GIS用户经常用以提取数据的手段之一。该方法源于传统的透明材料叠加,即将来自不同数据源的图纸绘于透明纸上,在透光桌上将图纸叠放在一起,然后用笔勾绘感兴趣的部分(即提取感兴趣的数据)。地图的叠置,按直观概念就是将两幅或多幅地图重迭在一起,产生新数据层和新数据层上的属性。新数据层或新空间位置上的属性就是各叠置地图上相应位置处各属性的函数。
一般情况下,为便于管理和应用开发地理信息(空间信息和属性信息),在建库时是分层进行处理的。也就是说,根据数据的性质分类,性质相同的或相近的归并到一起,形成一个数据层。例如,对于一个地形图数据库来说,可以将所有建筑物作为一个数据层,所有道路作为一个数据层,地下管线井作为另一个数据层等等。我们经常要将各数据层综合起来作分析,如对各管线井求取离它最近的道路并计算它离最近道路的距离,这类问题就需要对多层数据实施叠置来产生具有新特征的数据层。
7.3.1 栅格系统的叠加分析
栅格数据来源复杂,包括各种遥感数据、航测数据、航空雷达数据、各种摄影的图像数据,以及数字化和网格化的地质图、地形图、各种地球物理、地球化学数据和其它专业图像数据。叠加分析操作的前提是要将其转换为统一的栅格数据格式,且各个叠加层必须具有统一的地理空间,即具有统一的空间参考(包括地图投影、椭球体、基准面等),统一的比例尺以及具有统一的分辨率(刘湘南,2005)。
栅格叠加可以用于数理统计,如行政区划图和土地利用类型图叠加,可计算出某一行政区划内的土地利用类型个数以及各种土地利用类型的面积;可进行益本分析,即计算成本、价值等,如城市土地利用图与大气污染指数分布图、道路分布图叠加,可进行土地价格的评估与预测;可进行最基本的类型叠加,如土壤图与植被图叠加,可得出土壤与植被分布之间的关系图;可以进行动态变化分析以及几何提取等应用;在各类地质综合分析中,栅格方式的叠置分析也十分有用,很多种类的原始资料如化探资料、微磁资料等等,都是离散数据,容易转换成栅格数据,因而便于栅格方式的叠置分析。另外由于没有矢量叠加时产生细碎多边形的问题(这一点下面会详细解释),栅格方式的叠置产生的结果有时更为合理。
在栅格系统中,层间叠加可通过像元之间的各种运算来实现。设A,B,C等表示第一、第二、第三等各层上同一坐标处的属性值,f函数表示各层上属性与用户需要之间的关系,U为叠置后属性输出层的属性值,则
U=f(A,B,C……)
叠加操作的输出的结果可能是:各层属性数据的平均值(简单算术平均或加权平均等);
各层属性数据的最大值或最小值;算术运算结果;逻辑条件组合等。
基于不同的运算方式和叠加形式,栅格叠加变换包括如下几种类型(刘湘南,2005):
(1)局部变换:基于像元与像元之间一一对应得运算,每个像元都是基于它自身的运算,不考虑其他的与之相邻的像元。
(2)邻域变换:以某一像元为中心,将周围像元的值作为算子,进行简单求和、求平均值、最大值、最小值等。
(3)分带变换:将具有相同属性值的像元作为整体进行分析运算。
(4)全局变换:基于研究区域内所有像元的运算,输出栅格的每一个像元值是基于全区的栅格运算,这里像元是具有或没有属性值的栅格。
1.局部变换
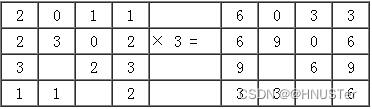
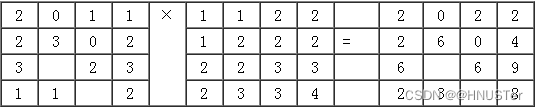
每一个像元经过局部变换后的输出值与这个像元本身有关系,而不考虑围绕该像元的其他像元值。如果输入单层格网,局部变换以输入格网像元值的数学函数计算输出格网的每个像元值,如图8-12所示。单层格网的局部变换可以是基本的代数运算,也可以是三角函数、指数、对数、幂等运算来定义其函数关系。多层格网的局部变换与把空间和属性结合起来的矢量地图叠置类似,但效率更高。输出栅格层的像元值可由多个输入栅格层的像元值或其频率的量测值得到,如图8-13。概要统计(包括最大值、最小值、值域、总和、平均值、中值、标准差等)也可用于栅格像元的测度。例如,用最大统计量的局部变换运算可以从代表20年降水变化的20个输入栅格层计算一个最大降水量格网,这20个输入栅格层中的每个像元都是以年降水数据作为其像元值。
2.邻域变换
邻域变换输出栅格层的像元值主要与其相邻像元值有关。如果要计算某一像元的值,就将该像元看作一个中心点,一定范围内围绕它的格网可以看作它的辐射范围,这个中心点的值取决于采用何种计算方法将周围格网的值赋给中心点,其中的辐射范围可自定义。若输入栅格在进行邻域求和变换时定义了每个像元周围3×3个格网的辐射范围,在边缘处的像元无法获得标准的格网范围,辐射范围就减少为2×2个格网,如图8-14所示。那么,输出栅格的像元值就等于它本身与辐射范围内栅格值之和。比如,左上角栅格的输出值就等于它和它周围像元值2、0、2、3之和7。
中心点的值除了可以通过求和得出之外,还可以取平均值、标准方差、最大值、最小值、极差频率等。邻域变换中的辐射范围一般都是规则的方形格网,也可以是任意大小的圆形、环形和楔形。圆形邻域是以中心点像元为圆心,以指定半径延伸扩展;环形或圈饼状邻域是由一个小圆和一个大圆之间的环形区域组成;楔形邻域是指以中心点单元为圆心的圆的一部分。
邻域变换的一个重要用途是数据简化。例如,滑动平均法可用来减少输入栅格层中像元值的波动水平,该方法通常用3×3或5×5矩形作为邻域,随着领域从一个中心像元移到另一个中心像元,计算出在邻域内的像元平均值并赋予该中心像元,滑动平均的输出栅格表示初始单元值的平滑化。另一个例子是以种类为测度的领域运算,列出在邻域之内有多少不同单元值,并把该数目赋予中心像元,这种方法用于表示输出栅格中植被类型或野生物种的种类。

3.分带变换
将同一区域内具有相同像元值得格网看作一个整体进行分析运算,称为分带变换。区域内属性值相同的格网可能并不毗邻,一般都是通过一个分带栅格层来定义具有相同值的栅格。分带变换可对单层格网或两个格网进行处理,如果为单个输入栅格层,分带运算用于描述地带的几何形状,诸如面积、周长、厚度和矩心。面积为该地带内像元总数乘以像元大小。连续地带的周长就是其边界长度,由分离区域组成的地带,周长为每个区域的周长之和。厚度以每个地带内可画的最大圆的半径来计算。矩心决定了最近似于每个地带的椭圆形的参数,包括矩心、主轴和次轴。地带的这些几何形状测度在景观生态研究中尤为有用。
多层栅格的分带变换如图8-15所示,通过识别输入栅格层中具有相同像元值得格网在分带栅格层中的最大值,将这个最大值赋给输入层中这些格网导出并存储到输出栅格层中。输入栅格层中有4个地带的分带格网,像元值为2的格网共有5个,它们分布于不同的位置并不相邻,在分带栅格层中,它们的值分别为1、5、8、3和5,那么取最大的值8赋给输入栅格层中像元值为2的格网,原来没有属性值的格网仍然保持无数据。分带变换可选取多种概要统计量进行运算,如平均值、最大值、最小值、总和、值域、标准差、中值、多数、少数和种类等,如果输入栅格为浮点型格网,则无最后四个测度。

4.全局变换
全局变换是基于区域内全部栅格的运算,一般指在同一网格内进行像元与像元之间距离的量测。自然距离量测运算或者欧几里德几何距离运算属于全局变换,欧几里德几何距离运算分为两种情况:一种是以连续距离对源像元建立缓冲,在整个格网上建立一系列波状距离带;另一种是对格网中的每个像元确定与其最近的源像元的自然距离,这种方式在距离量测中比较常见。
欧几里德几何距离运算首先定义源像元,然后计算区域内各个像元到最近的源像元的距离。在方形网格中,垂直或水平方向相邻的像元之间的距离等于像元的尺寸大小或者等于两个像元质心之间的距离;如果对角线相邻,则像元距离约等于像元的尺寸大小的1.4倍;如果相隔一个像元那么它们之间的距离就等于像元大小的2倍,其他像元距离依据行列来计算。如图8-16中,输入栅格有两组源数据,源数据1是第1组,共有三个栅格,源数据2组只有一个栅格。欧几里德几何距离定义源像元为0值,而其他像元的输出值是到最近的源距离像元的距离。因此,如果默认像元大小为1个单位的话,输出栅格中的像元值就按照距离计算原则赋值为0、1、1.4或2。

5.栅格逻辑叠加
栅格数据中的像元值有时无法用数值型字符来表示,不同专题要素用统一的量化系统表示也比较困难,故使用逻辑叠加更容易实现各个栅格层之间的运算。比如某区域土壤类型包括黑土、盐碱土以及沼泽土,也可获得同一地区的土壤pH值以及植被覆盖类型相关数据,要求查询出土壤类型为黑土、土壤pH值< 6且植被覆盖以阔叶林为主的区域,将上述条件转换为条件查询语句,使用逻辑求交即可查询出满足上述条件的区域。
二值逻辑叠加是栅格叠加的一种表现方法,用0和1分别表示假(不符合条件)与真(符合条件)。描述现实世界中的多种状态仅用二值远远不够,使用二值逻辑叠加往往需要建立多个二值图,然后进行各个图层的布尔逻辑运算,最后生成叠加结果图。符合条件的位置点或区域范围可以是栅格结构影像中的每一个像元,或者是四叉树结构影像中的每一个像块,也可以是矢量结构图中的每一个多边形。
图层之间的布尔逻辑运算包括:与(AND)、或(OR)、非(NOT)、异或(XOR)等。
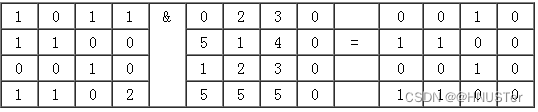
(1)与(&):比较两个或两个以上栅格数据图层,如果对应的栅格值均为非0值,则输出结果为真(赋为1),否则输出结果为假(赋值为0)。
(2)或(|):比较两个或两个以上栅格数据图层,对应的栅格值中只有一个或一个以上为非0值,则输出结果为真(赋为1),否则输出结果为假(赋值为0)。
(3)非(^):对一个栅格数据图层进行逻辑“非”运算,如果栅格值为0值,则输出结果为真(赋为1);如果栅格值为非0值,则输出结果为假(赋值为0)。
(4)异或(!):比较两个或两个以上栅格数据图层,如果对应的栅格值在逻辑真假互不相同(一个为0,另一个为非0值),则输出结果为真(赋为1),否则输出结果为假(赋值为0)。
6.栅格关系运算
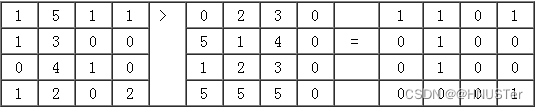
关系运算以一定的关系为基础,符合条件的为真,赋予1值;不符合条件的为假,赋予0值。关系运算符包括六种:=、<、>、<>、>= 和<=。
7.3.2 矢量系统的叠加分析(拓扑叠加)
矢量系统的叠加分析比栅格系统要复杂得多。拓扑叠加之前,假设每一层都是平面增
强的(已经建立了完整的拓扑关系),当两层数据叠加时,结果也必然应是平面增强的。当两线交叉时,要计算新的交叉点,一条线穿过某一区域时,必然产生两个子区域。
拓扑叠加能够把输入特征的属性合并到一起,实现特征属性在空间上的连接,拓扑叠加时,新的组合图的关系将被更新。
叠加可以是多边形对多边形的叠加(生成多边形数据层),也可以是线对多边形的叠加(生成线数据层)、点对多边形的叠加(生成点数据层)、多边形对点的叠加(生成多边形数据层),点对线的叠加(生成点数据层)。我们首先详细分析一下多边形与多边形的叠加。
1.多边形与多边形叠加
多边形与多边形合成叠加的结果,是在新的叠置图上,产生了许多新的多边形,每个多边形内都具有两种以上的属性。这种叠加特别能满足建立模型的需要。例如,将一个描述地域边界的多边形数据层叠加到一个描述土壤类别分界线的多边形要素层上,得到的新的多边形要素层就可以用来显示一个城市中不同分区的土壤类别。
由于两个多边形叠加时其边界在相交处分开,因此,输出多边形的数目可能大于输入多边形的总和。在多边形叠加操作中往往产生许多较小的多边形,其中有些并不代表实际的空间变化,这些小而无用的多边形称为碎多边形或伪多边形,它们是多边形叠加的主要问题,见下图。
伪多边形的产生原因是同一根线在两次输入的细微差异。如果同一条线在两张图上,数字化时必然有微小的差异,而且在大多数情况下,图上的线是根据不同来源的数据编辑而成,编辑时常常忽略它们是同一根线的事实(例如,道路可能是县界的一部分,同时也是两块地、两类土壤或植被的分界线)。即使数字化时尽量增加精度,也不能消除这一现象。有些系统允许用户设置一容差值,以消除叠加过程中产生的伪多边形,但这一容差值较难把握,因为容差过大,有些真实的多边形被删除;容差太小,又不能完全剔除错误的多边形。
多边形叠加的整个过程为(Tor Bernhardsen,2002):
(1)计算交叉点。
(2)形成结点和链。
多边形叠加是一个很耗时的处理过程。多边形叠加可以用来对数据进行一定地理区域的裁剪。例如,用一个专题图层中的乡镇边界去叠加所有其他的专题图层,从而只得到与该乡镇相关的所有数据。
多边形与多边形的叠加可以有合并(UNION)、相交(INTERSECT)、相减(SUBSTRACTION)、判别(IDENTITY)等方式。它们的区别在于输出数据层中的要素不同。合并保留两个输入数据层中所有多边形;相交则保留公共区域;相减从一个数据层中剔除另一个数据层中的全部区域;判别是将一个层作为模板,而将另一个输入层叠加在它上面,落在模板层边界范围内的要素被保留,而落在模板层边界范围以外的要素都被剪切掉。
2.线对多边形叠加
线对多边形叠加的结果是一些弧段,这些弧段也具有它们所在的多边形的属性。例如,公路以线的形式作为一层,将它与另一层的县界多边形作叠加,其结果能够用来决定每条公路落在不同县内的公里长度。线对多边形叠加可以有相交、判别、相减等方式,叠加结果分别是穿过多边形的线要素部分、所有线要素(被多边形切断)、多边形以外的线要素。
3.点对多边形叠加
点对多边形叠加实质是计算包含关系,叠加结果是一串带有附加属性的点要素,点所在的多边形的属性被连接到点的属性中。例如,井的位置以点要素的形式作为一层土地租用分区以多边形要素的形式记录在另一层,那么这两层作点对多边形叠加的结果可以用来确定井在各土地租用区内的分布。点对多边形叠加也可以有相交、判别、相减等方式,叠加结果分别是落在多边形内的点要素、所有点要素、多边形以外的点要素。
4.多边形对点叠加
多边形对点叠加的结果是多边形,但只保留那些有点落在上面的多边形,这种叠加不作属性连接,结果多边形的属性和原始多边形相同。
5.点对线叠加
点对线叠加的结果为点要素,它保留所有点,找到距离某点最近的线并计算出点线之间的距离,然后将线号和点线距离记录到该点的属性中。
7.4 缓冲分析
在GIS的空间操作中,涉及到确定不同地理特征的空间接近度或临近性的操作就是建立缓冲区。例如在林业方面,要求距河流两岸一定范围内规定出禁止砍伐树木的地带,以防止水土流失;又例如,城市道路扩建需要推倒一批临街建筑物,于是要建立一个距道路中心线一定距离的缓冲区,落在缓冲区内的建筑就是必须拆迁的。
7.4.1 缓冲分析概念
缓冲分析就是在点、线、面实体(缓冲目标)周围建立一定宽度范围的多边形。换言之,任何目标所产生的缓冲区总是一些多边形,这些多边形将构成新的数据层。

上图显示了单个点、单个线或单个面的缓冲区。如果缓冲目标是多个点(或多个线、多个面),则缓冲分析的结果是各单个点(线、面)的缓冲区的合并,碰撞到一起的多边形将被合并为一个,也就是说,GIS可以自动处理两个特征的缓冲区重迭的情况,取消由于重迭而落在缓冲区内的弧段。见下图。

根据地理实体的性质和属性,对其规定不同的缓冲区距离,通常是十分必要的。例如,沿河流两岸绘出的禁止砍伐树木带的宽度应根据河流类型以及两岸土质而定。因此,GIS系统应有求取可变缓冲区的能力,例如允许用户在属性表中定义一项,作为缓冲区宽度,见上图。
7.4.2 建立缓冲区的算法
建立缓冲区的实质是做面、线、点状地物的扩展距离图。
1.点缓冲区算法
等距离的点缓冲区是一个圆。
2.线缓冲区和面缓冲区的基本算法
(1)角平分线法
角平分线法建立线缓冲区和面缓冲区的实质是在线的两边按一定距离(称缓冲距)做平行线,在线的端点画半圆相连。
在求算过程中,当直线相接处(拐点)出现凸角时需要做特殊处理。如下图中,凸角处做平行线将出现过长的尖角,在尖角处出现超过规定缓冲距问题,为此,应除去尖角,代之以半圆。

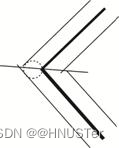
(2)凸角圆弧法
凸角圆弧法将线的拐点求出凹凸性,凸侧用圆弧弥合法,以防角平分线法中出现尖角;凹侧用角平分法建立,如下图所示。
3.复杂缓冲区的生成
对复杂曲线、曲面建立缓冲区时,经常会出现缓冲区重叠问题,这时,需要通过对缓冲区边界求交,除去重叠部分,或通过对缓冲区边界求交,对建立缓冲区所生成的图形进行判断,除去缓冲区内部线,将缓冲区组成连通区。
7.5 网络分析
网络是地理信息系统(GIS)中一类独特的数据实体,它由若干线性实体通过结点连结而成。网络分析是空间分析的一个重要方面,是依据网络拓扑关系(线性实体之间,线性实体与结点之间,结点与结点之间的连结、连通关系),并通过考察网络元素的空间、属性数据,对网络的性能特征进行多方面的分析计算。
与GIS的其它分析功能相比,关于网络分析的研究一直比较少,但是近年来由于普遍使用GIS管理大型网状设施(如城市中的各类地下管线、交通线、通讯线路等),使得对网络分析功能的需求迅速发展,GIS平台软件纷纷推出自己的网络分析子系统。
7.5.1 网络数据模型――几个基本概念
网络是由若干线性实体互连而成的一个系统,资源经由网络来传输,实体间的联络也经由网络来达成。网络数据模型是真实世界中网络系统(如交通网、通迅网、自来水管网、煤气管网等)的抽象表示。构成网络的最基本元素是上述线性实体以及这些实体的连接交汇点。前者常被称为网线或链(link),后者一般称为结点(node)。
网线构成网络的骨架,是资源传输或通讯联络的通道,可以代表公路、铁路、航线、水管、煤气管、河流等等;结点是网线的端点,又是网线汇合点,可以表示交叉路口、中转站、河流汇合点等。
除了上述基本网络元素之外,由于分析任务的不同,网络还可能有若干附属元素,如在路径分析中用来表示途经地点的可以进行资源装卸的站点(stop);在资源分配中用来表示资源发散地点或资源汇聚地点的中心(center),对资源传输或通讯联络起阻断作用的障碍(barrier)等等。
由于通用性的不同以及网络分析功能的侧重点不同,各个地理信息系统的网络模型也不尽相同,差异主要体现在对网络附属元素的分类和设定上。
针对网络分析的需要,作为网络基本元素的网线或结点除自身的常规属性外,还要具有一些特殊的属性数据。比如,为了实施路径分析和资源分配,网线数据应包含正反两个方向上的阻碍强度(如流动时间、耗费等)以及资源需求量(如学生人数、水流量、顾客量等),而结点数据也应包括资源需求量。特别应该指出的是,在有些GIS平台(如ARC/INFO、MAPGIS)中,结点还可以具有转角数据,从而可以更加细致地模拟资源流动时的转向特性。具体地说,每个结点可以拥有一个转向表(turntable),其中的每一项说明了资源从某一网线经该结点到另一网线时所受的阻碍强度。
对于附属的网络元素,与其相关的数据则主要用来满足网络分析的需要。与中心相联系的数据包括该中心的资源容量、阻碍限度(资源流出或流向该中心所能克服的最大累积阻碍),有些GIS系统还允许赋予中心一定的延迟量,以表达该中心相对于其它中心进行资源分配的优先程度。与站点相关的数据一般有传输量(即资源装卸量)、阻碍强度。障碍一般无需任何相关数据。
以上所讨论的,是在GIS特别是通用GIS平台中较为广泛采用的网络模型及相关概念,正如前面所说,不同的GIS系统的网络模型往往会在网络附属元素的设定和运用方面体现出自身的特色。对于网络分析系统的设计研制者而言,重要的问题在于建立一个抽象的、具有相当适应面的,并且也是便于实现分析任务的网络模型;而对于这一系统的使用者而言,关键之处在于:深入理解现实网络系统中各个组成部分的特点及其相互关系,明确自身的管理分析任务,在此基础上,用网络模型中的不同元素合理地表示这些组成成分。
7.5.2 常规的网络分析功能
虽然各个GIS系统的网络分析功能有所不同,但有些分析功能是用户经常需要的,以下是常见的网络分析功能。
1.路径分析
路径分析是GIS中最为普遍的也是基本的功能,其核心是对最佳路径和最短路径的求解。救护车需要了解从医院到病人家里走哪条路最快;旅客往往要在众多航线中找到费用最小的中转方案,这些都是最佳路径求解的例子。从网络模型的角度看,最佳路径求解就是在指定网络中两结点间找一条阻碍强度最小的路径。最佳路径的产生基于网线和结点转角(如果模型中结点具有转角数据的话)的阻碍强度。例如,如果要找最快的路径,阻碍强度要预先设定为通过网线或在结点处转弯所花费的时间;如果要找费用最小的路径,阻碍强度就应该是费用。当网线在顺逆两个方向上的阻碍强度都是该网线的长度,而结点无转角数据或转角数据都是零时,最佳路径就成为最短路径。
最短路径分析需要计算网络中从起点到终点所有可能的路径,从中选择一条到起点距离最短的一条。用于最短路径分析的算法很多,其中最著名的是Dijkstra算法(Dijkstra, 1959),该算法可描述如下:
设一个网络由可k个结点组成,以N ={ni=1,2,…,k}表示结点集,其中一个结点为起始结点,设其为ns。Dijkstra算法将N划分成两个子集,一个子集包含那些到起始结点的最短距离已确定的结点,称这些结点为已确定结点,以s表示这一子集;另一个子集包含未确定结点,即它们到起始结点的最短距离尚未确定,以Q表示这一子集。又设d为一个距离矩阵(array),存放每个结点到ns的最短距离,d(i)表示结点ni到ns的最短距离;p为一前置结点矩阵,存放由ns到其他结点的最短路径上每个结点的前一个结点,p(i)表示结点ni在最短路径上的前一个结点。已知每两个相连结点之间的距离(或它们之间路径的长度),Dijkstra算法按如下几个步骤运行:
(1)将d和p初始化,使d的每个元素值为无穷大,p的每个元素值为空值,并设S和Q为空集;
(3)从Q中找出到ns最短距离为最小的结点,设该结点为nu;
(5)找出与nu相连的所有结点,从这些结点中取出一个,令其为nv,
① 如nv已存在于s中,则执行下面第②步,否则,作如下判断:
如果d(v) < d(u) + n-u和nv之间的距离,执行第②步;
否则{令d(v) = d(u) + nu和nv之间的距离;
p(v)=nu;
将nv加进Q;
② 如果与nu相连的所有结点都已作过上述判断,继续执行第(6)步;否则,取下一个未判断结点,令其为nv,执行上面的第①步;
(6)判断Q是否为空集,若不是,回到第(3)步;否则,停止运算。
在某些情况下,用户可能要求系统能一次求出所有结点之间的最佳路径,或者要了解两结点间的第二、第三乃至第K条最佳路径。这种需求的提出往往是由于现有网络模型不能包容所有特殊或突发的情况。
另一种路径分析功能是最佳游历方案(包括网线游历和结点游历)的求解。警察需要了解巡查完他担任巡逻的各个街道的最有效线路,铁路巡道员也需要知道巡查完他的路轨的最佳路线,这些都是网线最佳游历方案求解的例子,也就是给定一个网线集合和一个结点,求解最佳路径,使之由指定结点出发至少经过每条网线一次而回到起始结点。结点最佳游历方案求解,则是给定一个起始结点、一个终止结点和若干中间结点,求解最佳路径,使之由起点出发遍历全部中间结点而达终点。推销员可以利用求解结果以尽可能最少的旅程遍访其所分配的每一座城市;商场送货车每天送大量的商品到各个居民点,司机也想知道怎么安排行程最快。
2.资源分配
资源分配就是为网络中的网线和结点寻找最近(这里的远近是按阻碍强度的大小来确定的)的中心(资源发散或汇集地)。例如,资源分配能为城市中的每一条街道上的学生确定最近的学校,为水库提供其供水区,等等。资源分配模拟资源是如何在中心(学校,消防站,水库等)和它周围的网线(街道,水路等)、结点(交叉路口,汽车中转站等)间的流动的。
资源分配根据中心容量以及网线和结点的需求将网线和结点分配给中心,分配是沿最佳路径进行的。当网络元素被分配给某个中心,该中心拥有的资源量就依据网络元素的需求而缩减,当中心的资源耗尽,分配就停止。
考虑这样一个问题:一所学校要依据就近入学的原则来决定应该接收附近那些街道上的学生。这时,可以将街道作为网线构成一个网络,将学校作为一个结点并将其指定为中心,以学校拥有的座位数作为此中心的资源容量,每条街道上的适龄儿童作为相应网线的需求,走过每条街道的时间作为网线的阻碍强度,如此资源分配功能就将从中心出发,依据阻碍强度由近及远地寻找周围的网线并把资源分配给它(也就是把学校的座位分配给相应街道上的儿童),直至被分配网线的需求总和达到学校的座位总数。
用户还可以通过赋给中心的阻碍限度来控制分配的范围。例如,如果限定儿童从学校走回家所需时间不能超过30分钟,就可以将这一时间作为学校对应的中心的阻碍限度,这样,当从中心延伸出去的路径的阻碍值到达这一限度时分配就将停止,即使中心资源尚有剩余。
3.连通分析
人们常常需要知道从某一结点或网线出发能够到达的全部结点或网线。例如,当地震发生时,救灾指挥部需要知道,把所有被破坏的公路和桥梁考虑在内,救灾物资能否从集散地出发送到每个居民点,如果有若干居民点与物资集散地不在一个连通分量之内,指挥部就不得不采用特殊的救援方式(如派遣直升机)。这一类问题称为连通分量求解。
另一连通分析问题是最少费用连通方案的求解问题,例如,公路部门拟修建足够数量的公路,使某个县的五个镇直接或间接地相互连结,如何使费用最少呢?如果把每一条可能修建的公路作为网线,把相应的预算费用作为网线的耗费,上述问题就转化为求一个网线集合,使全部结点连通且总耗费最少。
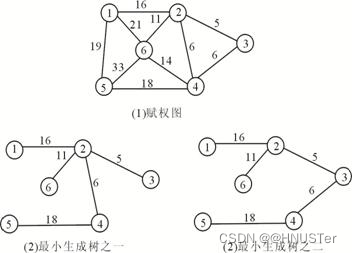
在实际应用中,常有类似在n个城市间建立通信线路这样的问题。这可用图来表示,图的顶点表示城市,边表示两城市间的线路,边上所赋的权值表示代价。对n个顶点的图可以建立许多生成树,每一棵树可以是一个通信网。若要使通信网的造价最低,就需要构造图的最小生成树(图8-29)。
生成树是图的极小连通子图。一个连通的赋权图G可能有很多的生成树。设T为图G的一个生成树,若把T中各边的权数相加,则这个和数称为生成树T的权数。在G的所有生成树中,权数最小的生成树称为G的最小生成树。
构造最小生成树的依据有两条:
② 尽可能选取权值为最小的边。
下面介绍构造最小生成树的克罗斯克尔(Kruskal)算法。该算法是1956年提出的,俗称“避圈”法。设图G是由m个节点构成的连通赋权图,则构造最小生成树的步骤如下:
① 先把图G中的各边按权数从小到大重新排列,并取权数最小的一条边为T中的边。
② 在剩下的边中,按顺序取下一条边。若该边与T中已有的边构成回路,则舍去该边,
否则选进T中。
③ 重复②,直到有m-1条边被选进T中,这m-1条边就是G的最小生成树。
例:设有如图8―29(1)所示的图,图的每条边上标有权数。为了使权数的总和为最小,应该从权数最小的边选起。在此,选边(2,3);去掉该边后,在图中取权数最小的边,此时,可选(2,4)或(3,4),设取(2,4);去掉(2,4)边,下一条权数最小的边为(3,4),但使用边(3,4)后会出现回路,故不可取,应去掉边(3,4);下一条权数最小的边为(2,6);依上述方法重复,可形成图8-29(2)所示的最小生成树。如果前面不取(2,4),而取(3,4),则形成图8-29(3)所示的最小生成树。
4.流分析
所谓流,就是将资源由一个地点运送到另一个地点。流分析的问题主要是按照某种最优化标准(时间最少、费用最低、路程最短或运送量最大等)设计运送方案。
为了实施流分析,就要根据最优化标准的不同扩充网络模型。要把中心分为收货中心和发货中心,分别代表资源运送的起始点和目标点。这时发货中心的容量就代表待运送资源量,收货中心的容量代表它所需要的资源量。网线的相关数据也要扩充,如果最优化标准是运送量最大,就要设定网线的传输能力;如果目标是使费用最低,则要为网线设定传输费用(在该网线上运送一个单位的资源所需的费用)。
5.选址
选址功能涉及在某一指定区域内选择服务性设施的位置,例如市郊商店区、消防站、工厂、飞机场、仓库等的最佳位置的确定。在网络分析中的选址问题一般限定设施必须位于某个结点或位于某条网线上,或者限定在若干候选地点中选择位置。存在种类繁多的选址问题,实现方法和技巧也多种多样,不同GIS系统在这方面各有特色。造成这种多样性的原因主要在于:对“最佳位置”的解释(即用什么标准来衡量一个位置的优劣)以及要定位的是一个设施还是多个设施。
由于存在大量的各种各样的选址问题,所以有关文献中也有各种各样的选址问题的数学模型及求解方法。(边馥苓,2006)这里讨论的仅限于选址的范围是一个网络图,而且选址位置必须位于网络图的某一个或几个顶点上,亦可位于一条边的某一个位置上。选址问题又可以分为求网络图的中心点与中位点两类问题。
(1)中心点选址问题
中心点选址问题是使最佳选址位置所在的顶点与图中其他顶点之间的最大距离达到最 小。这类选址问题适宜于学校、医院、消防站点等一类服务设施的布局问题。例如,某镇要在其所辖的几个村之一修建一个初中,为这几个村服务,要求学校至最远村的距离达到最小。这类选址问题,实际上就是求网络图的中心点问题。
(2)中位点选址问题
中位点选址问题是使最佳选址位置所在的顶点到网络图中其他顶点的距离(亦可以是加权距离)总和达到最小。
例如某超市要确定一个配送中心,要使该中心到超市各分店的距离最短,这就是一个典型的中位点选址问题。
除以上所述之外,还有诸如关阀搜索、上下游追踪、空间排序、可访问性分析等网络分析功能。
7.6 地理信息系统的数学模型
利用计算机解决地理信息系统中的各种实际问题时,最重要的工作是建立地理系统的数学模型,并使建立的模型能较好地模拟实际事物的属性和规律。正如一张地形图上,如果漏绘了一些道路,或者标错了某些山顶的高程,将会给部队指挥和行军作战造成严重后果,说明这张地形图(也可称为符号模型)错误地描述了实际事物。对于数学模型来说,除了具有物理模拟的特征外,还需要具有数学方法的抽象模拟,利用数学符号、数学式子、程序等刻画实际事物的客观本质属性及其内在联系规律。本章首先介绍建立数学模型的一般过程,然后介绍常见的数理统计模型、回归分析模型和线性规划模型。
7.6.1 建立数学模型的一般过程
面对着复杂的现实世界,各种事物都处在不断的变化之中,要用数学方法去描述和模拟某些发展中的现象,不可能采用统一的模式来论述建模问题。但是,可以把建模过程大致划分下列几个步骤:
在调查研究过程中,尽可能掌握与建模有关的数据和资料。应当访问建模对象所在领域的专家,认真总结他们在科学研究中的思路和方法以及解决问题的推理判断过程。这些专家的逻辑思维经验是十分可贵的第一手建模材料,甚至有些经验已经构成了物理模拟的框架,这些都是建立数学模型的基础。
抓住主要问题分解模拟对象,提出可能性较大的几种假设,尽可能使问题简化,减少考虑的因素。这一过程就是数学抽象和思维的过程。建模者应当具备这种抽象、假设能力,同时需要与该领域的专家共同讨论,使假设的现实性增加,避免一些不必要的建模工作的重复过程。
3.数据处理
通过实地调查或测量,采集必要的数据,输入计算机,建立数据库。
利用某些绘图软件或采用统计回归分析的方法,调用已知数据,作出曲线图,用已知曲线拟合实际曲线。
5.模型建立
简化实际问题,提出恰当的假设,并利用适当的数学工具,刻划变量之间的关系,建立相应的数学模型,并求得相应的解。
6.模型的验证
将模型运算结果与实际情况相比较,也就是进行误差分析,确定模型的可信程度。如果计算结果与事实不相符合,说明在建模的过程中,可能忽略了某些重要的因素,缺乏关键的数据。这时,必须加强对实际问题的调研,重新开始建模过程。
7.预测和决策
一个成功的地理信息系统的数学模型,不仅能解释系统的已知现象,而且还可以预测系统的某些未知现象,把已知数据代入模型内,预测系统的发展趋势,并为系统的合理利用与开发,提供最优决策。
7.6.2 数理统计分析模型
数理统计分析主要用于数据分类和综合评价,数据的分类和评价的问题通常涉及大量的相互关联的地理因素。主成分分析方法可以从统计意义上将各影响要素的信息压缩到若干合成因子上,从而使模型大大地简化。因子权重的确定是建立评价模型的重要步骤,权重正确与否极大地影响评价模型的正确性,而通常的因子权重的确定依赖较多的主观判断。层次分析法是综合众人意见,科学地确定各影响因子权重的简单而有效的数学手段。隶属度反映因子内各类别对评价目标的不同影响,依据不同因子内的变化情况确定,常采用分段线性函数或其它高次函数形式计算。常用的分类和综合的方法包括聚类分析和判别分析两大类。聚类分析可根据地理实体之间影响要素的相似程度,采用某种与权重和隶属度有关的距离指标,将评价区域划分若干类别;判别分析类似于遥感图像处理的分类方法,即根据各要素的权重和隶属度,采用一定的评价标准将各地理实体判归最可能的评价等级或以某个数据值所示的等级序列上。分类定级是评价的最后一步,将模糊聚类的结果根据实际情况进行合并,并确定合并后每一类的评价等级,对于模糊判别分析的结果序列采用等间距或不等间距的标准划分为最后的评价等级。
下面简要介绍分类评价中常用的几种数学方法。
1.主成分分析
在地理问题中,指标越多,问题分析就越复杂,但实际的指标并不一定都是独立无关的,恰恰相反,许多指标之间存在着相当好的相关性。因此,力求用较少的指标来进行分析研究,并要求指标同样能反映原有较多指标的信息。找出较少指标就是要找出少数几个独立无关的变量,这种方法称之为主成分分析。
2.层次分析法
过去研究自然或社会现象主要有机理分析和统计分析两种方法。前者用经典的数学工具分析现象的因果关系,后者以随机数学为工具,通过大量的观测数据寻求统计规律。近年来发展起来的第三种方法称系统分析。层次分析(AHP)法就是系统分析的数学工具之一,它把人的思维过程层次化、数量化,并用数学方法为分析、决策预报或控制提供定量的数据。事实上这是一种定性和定量分析相结合的方法。在模型涉及大量相互关联、相互制约的复杂因素的情况下,各因素对问题的分析有着不同的重要性,决定它们对目标重要性的序列,对建立模型十分重要。AHP方法把相互关联的要素按隶属关系分为若干层次,请有经验的专家对各层次各因素的相对重要性综合定量指标,利用数学方法综合专家意见给出各层次各要素的相互重要性权值,作为综合分析的基础。
3.系统聚类分析
虽然数据整理能将大量而复杂的多变量数据适当压缩,但人们希望进一步减少数据的复杂程度,即将数据定义成一组多变量类别。主成分分析仅仅是数据沿着一条新轴的旋转和投影,得到新值,既大大压缩了原始数据也可以作为新变量使用。主成分分析后的主分量不是按地理空间制图,而是按主成分轴定义的空间制图。当数据在主成分空间的两坐标轴上的分布具有相似性时,这种散射图(常把主成分空间绘制的图称散射图)能够显示出明显的类别特性即聚类特性。如果这些聚类能归纳为分类系统中的某一类的话,就有可能进一步减少数据的复杂性。另外,这些聚类完全由原始数据的分析推演而得,因而能代表“天然”类别,比外生分类(按所研究数组的门槛确定其区间,而不是由数组本身派生出来的区间)和层次分类等人为强加的类别更加真实。
60年代末到70年代初人们把大量精力集中于发展和应用数学分类法,且将这类方法应用于自然资源、土壤剖面、气候分类、环境生态等数据,形成“数学分类学”学科。目前聚类分析已成为标准的分类技术,在许多大型计算机中都存储了这种分析程序,从GIS数据库中将点数据传送到聚类分析程序也不困难。
聚类分析的主要依据是把相似的样本归为一类,而把差异大的样本区别开来。在由m个变量组成的m维的空间中,可以用多种方法定义样本之间的相似性和差异性统计量。它是一种定量方法,从数学分析的角度,给出一个更准确、细致的分类。
4.判别分析
判别分析的特点是根据已掌握的、历史上每个类别的若干样本的数据信息,总结出客观事物分类的规律性,建立判别公式和判别准则,就能判别该样本所属的类别。例如,在评价产品的市场竞争力时,可根据商品的多项指标(诸如其内在质量、外型美观以及包装、价格等)判别消费者对商品喜欢或 判别分析依其判别类型的多少与方法的不同,可分为两总体判别、多总体判别和逐步判别等。
7.6.3 回归分析模型
回归分析是研究因变量y和自变量x之间存在某种相关关系的方法,其中要求自变量x是可以控制或可以精确观察的变量,因此当x取每一个确定值后,y就有一定的概率分布。若y的数学期望存在,则其值是x的函数。即y=μ(x),这个μ(x)称为y对x的回归函数,或称y关于x的回归。回归函数可以是一元函数,也可以是多元函数,可以是线性的,也可以是非线性的。
7.7 习题
1.地理信息系统(GIS)与计算机辅助绘图系统(CAC)的主要区别是什么?
2.空间分析的一般步骤是怎样的?
(1)公园的位置既要交通便利又要环境安静,也就是说距主要公路的距离要适当。
(2)公园应设计成环绕一个天然的小河流。
(3)使公园的可利用面积最大,公园中应很少或没有沿河流分布的沼泽地。
假设已经准备好了下面几层数据:穿过研究区的公路(线要素层)、位于研究区内的河段(线要素层,用分类级别CLASS标识,CLASS为2的河段,其特性适合于建立公园)、位于研究区内的沼泽地(区要素层)。我们的目的是确定一些具体的河段,作为建立公共郊游公园的可能位置。为了达到上述三条选址标准,应进行哪些空间操作?
5.如果利用本节中讨论的网络数据模型来模拟城市公路的分布和公路间的连接关系,如何表现单行道?如何表示禁止向某方向转弯的路口?如何表示发生阻塞的路口?
6.大中城市一般由多个自来水厂供水,整个城市的供水管道形成连通的管网,如果要运用资源分配来查看整个城市的自来水供水状况,试设计相应的网络模型。
8.建立地理信息系统的数学模型一般分哪几步?
原文地址:https://blog.csdn.net/ZK180531/article/details/134748063
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。
如若转载,请注明出处:http://www.7code.cn/show_35820.html
如若内容造成侵权/违法违规/事实不符,请联系代码007邮箱:suwngjj01@126.com进行投诉反馈,一经查实,立即删除!