0. 简介
归并排序(Merge Sort)是一种分治思想的应用,它将待排序的数组不断拆分成小数组,直到每个小数组只有一个元素,然后将小数组两两合并,直到最终得到有序的数组。
1. 归并排序的实现
归并排序的基本思想:
- 分解:将待排序的数组从中间分成两部分,递归地对左右两部分进行分解,直到每个小数组只有一个元素,这时可以认为每个小数组是有序的。
- 解决:将两个有序的小数组合并成一个有序的数组。可以使用双指针法,比较两个数组的元素大小,按照从小到大的顺序将元素放入新的数组中。
- 合并:递归地将左右两个有序的数组合并成一个更大的有序数组,直到最终得到整个有序数组。
归并排序过程演示:
2. 归并排序时空间复杂度分析
-
空间复杂度:
综上所述,归并排序的时间复杂度是 O(n log n),空间复杂度是 O(n)。
3. 归并排序C语言代码
C代码实现:
#include <stdio.h>
// 合并两个有序数组
void merge(int arr[], int l, int m, int r) {
int i, j, k;
int n1 = m - l + 1;
int n2 = r - m;
// 创建临时数组
int L[n1], R[n2];
// 将数据拷贝到临时数组
for (i = 0; i < n1; i++)
L[i] = arr[l + i];
for (j = 0; j < n2; j++)
R[j] = arr[m + 1 + j];
// 合并临时数组到原数组
i = 0;
j = 0;
k = l;
while (i < n1 && j < n2) {
if (L[i] <= R[j]) {
arr[k] = L[i];
i++;
} else {
arr[k] = R[j];
j++;
}
k++;
}
// 将剩余元素拷贝到原数组
while (i < n1) {
arr[k] = L[i];
i++;
k++;
}
while (j < n2) {
arr[k] = R[j];
j++;
k++;
}
}
// 归并排序函数
void mergeSort(int arr[], int l, int r) {
if (l < r) {
int m = l + (r - l) / 2; // 计算中间位置
mergeSort(arr, l, m); // 对左半部分递归排序
mergeSort(arr, m + 1, r); // 对右半部分递归排序
merge(arr, l, m, r); // 合并左右两部分
}
}
// 测试代码
int main() {
int arr[] = { 12, 11, 13, 5, 6, 7 };
int arr_size = sizeof(arr) / sizeof(arr[0]);
mergeSort(arr, 0, arr_size - 1); // 对数组进行归并排序
printf("Sorted array:n");
for (int i = 0; i < arr_size; i++) {
printf("%d ", arr[i]);
}
printf("n");
return 0;
}代码解释:
int n1 = m - l + 1;和int n2 = r - m;:这两行代码计算两个子数组的长度。n1是左子数组的长度,n2是右子数组的长度。int L[n1], R[n2];:我们创建两个临时数组L和R来存储左子数组和右子数组的元素。- 接下来的两个循环将左子数组和右子数组的元素拷贝到临时数组
L和R中。 - 然后,我们使用三个指针
i,j, 和k来合并这两个有序的子数组。指针i和j分别指向临时数组L和R的当前元素,而指针k指向原数组arr的当前位置。 - 在合并的过程中,我们比较
L[i]和R[j]的值,并将较小的元素放入原数组arr中。这个过程会一直持续到我们遍历完L或R中的所有元素。 - 最后,我们将剩余的元素(如果有的话)从
L或R拷贝到原数组arr中。
if (l < r) { ... }:这个条件用于判断数组是否至少包含两个元素。如果只有一个元素或没有元素,那么数组已经是有序的,不需要进一步排序。int m = l + (r - l) / 2;:这行代码计算数组的中间位置。我们通过将数组的长度(r - l)除以 2 并加上起始索引l来得到中间位置m。mergeSort(arr, l, m);和mergeSort(arr, m + 1, r);:这两行代码递归地对左子数组和右子数组进行排序。递归的终止条件是子数组的长度为 1 或 0。merge(arr, l, m, r);:当左子数组和右子数组都被排序后,我们使用merge函数将它们合并成一个有序的数组。
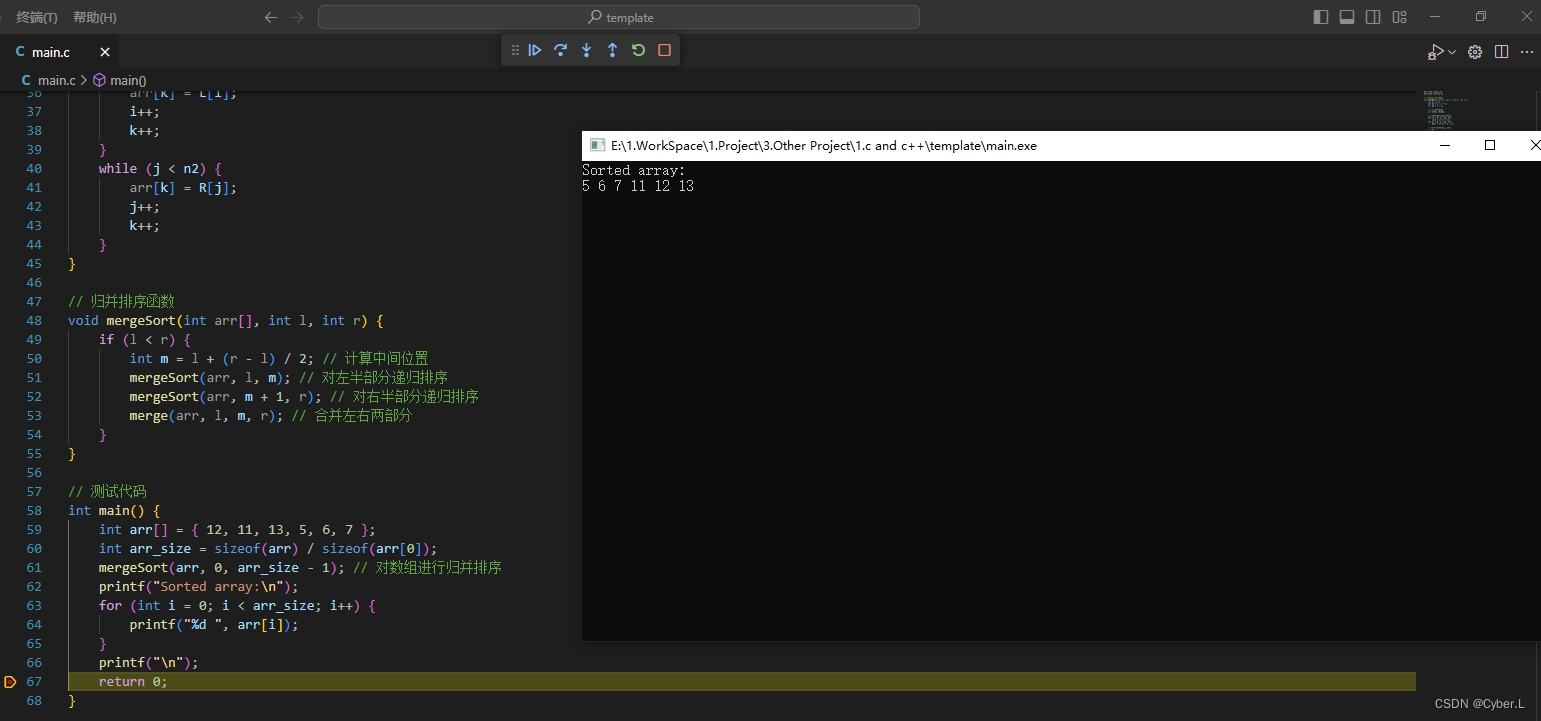
4. 归并排序代码运行结果
代码运行结果:
原文地址:https://blog.csdn.net/Liu_eight_nine/article/details/134764357
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。
如若转载,请注明出处:http://www.7code.cn/show_36474.html
如若内容造成侵权/违法违规/事实不符,请联系代码007邮箱:suwngjj01@126.com进行投诉反馈,一经查实,立即删除!
声明:本站所有文章,如无特殊说明或标注,均为本站原创发布。任何个人或组织,在未征得本站同意时,禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益,可联系我们进行处理。