论文:ROFORMER: ENHANCED TRANSFORMER WITH ROTARY POSITION EMBEDDING
作者:Jianlin Su, Yu Lu, Shengfeng Pan, Ahmed Murtadha, Bo Wen, Yunfeng Liu
时间:2021
地址:https://huggingface.co/docs/transformers/model_doc/roformer
一、完整代码
由于Transformer是老生常谈了,这里我们只简要实现RoPE
# 完整代码在这里
class RotaryEmbedding(tf.keras.layers.Layer):
def __init__(
self,
max_wavelength=10000,
scaling_factor=1.0,
sequence_axis=1,
feature_axis=-1,
**kwargs
):
super().__init__(**kwargs)
self.max_wavelength = max_wavelength
self.sequence_axis = sequence_axis
self.feature_axis = feature_axis
self.scaling_factor = scaling_factor
self.built = True
def call(self, inputs, start_index=0):
rotary_dim = tf.shape(inputs)[-1]
cos_emb, sin_emb = self._compute_cos_sin_embedding(
inputs, rotary_dim, start_index
)
return self._apply_rotary_pos_emb(inputs, cos_emb, sin_emb)
def _apply_rotary_pos_emb(self, tensor, cos_emb, sin_emb):
x1, x2 = tf.split(tensor, 2, axis=self.feature_axis)
half_rot_tensor = tf.concat((-x2, x1), axis=self.feature_axis)
return (tf.matmul(tensor,cos_emb)) + (tf.matmul(half_rot_tensor, sin_emb))
def _compute_cos_sin_embedding(self, x, rotary_dim, start_index):
freq_range = tf.range(0, rotary_dim, 2, dtype="float32")
freq_range = tf.cast(freq_range, self.compute_dtype)
freq_range = freq_range / tf.cast(
self.scaling_factor, self.compute_dtype
)
inverse_freq = 1.0 / (
self.max_wavelength
** (freq_range / tf.cast(rotary_dim, self.compute_dtype))
)
seq_len = tf.shape(x)[self.sequence_axis]
tensor = tf.range(seq_len, dtype="float32") + start_index
tensor = tf.cast(tensor, dtype=inverse_freq.dtype)
freq = tf.einsum("i, j -> ij", tensor, inverse_freq)
embedding = tf.concat((freq, freq), axis=self.feature_axis)
def get_axis(axis):
return axis if axis > 0 else len(x.shape) + axis
feature_axis = get_axis(self.feature_axis)
sequence_axis = get_axis(self.sequence_axis)
for axis in range(len(x.shape)):
if axis != sequence_axis and axis != feature_axis:
embedding = tf.expand_dims(embedding, axis)
return tf.cos(embedding), tf.sin(embedding)
二、论文解读
RoPE通过其特性优先于现有的位置编码方法,包括序列长度的灵活性、随着相对距离的增加而减少的标记间依赖性,以及用相对位置编码装备线性自注意的能力。在各种长文本分类基准数据集上的实验结果表明,具有RoPE嵌入的Transformer,即RoFormer,具有更好的性能;
RoPE的关键思想是通过将上下文表示与一个旋转矩阵相乘来获取元素的相对位置;
2.1 注意力机制

2.2 绝对位置编码
这个是最普通的Transformer采取的编码方式,非常的经典;

2.3 相对位置编码
下图是Transformer-XL采取的编码方式,其目的是为了避免在循环机制中出现位置混淆;

下面两个是Exploring the Limits of Transfer Learning with a Unified Text-to-Text Transformer采取的编码方式;

i
,
j
b_{i,j}
bi,j进行嵌入,自由度非常大;
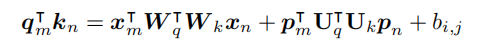
DeBERTa: Decoding-enhanced BERT with Disentangled Attention这篇论文中认为常规注意力机制中的
m
T
⋅
W
q
T
⋅
W
⋅
n
pmT⋅WqT⋅Wk⋅pn并没有表达相对信息,只是做一个bias的作用,而bias在
q
,
,
q,k,v
q,k,v时就已经体现,不需要bias,采取删除的方法,然后把绝对位置信息转化为相对位置信息;

论文说Radford and Narasimhan(这两货是GPT模型的提出者)在2018年的时候对这四种变体进行了比较,发现第四个相对位置编码即删除了bias的相对位置编码最为合理;但让我纳闷的是这不是2020年的论文吗?
2.4 旋转位置编码
旋转位置编码RoPE的关键思想是通过将上下文表示与一个旋转矩阵相乘来编码相对位置;
q
m
T
k
n
q_m^Tk_n
qmTkn 只与
x
m
x_m
xm ,
x
n
x_n
xn 以及其相对位置
m
−
n
m-n

但凡提到旋转Rotary,肯定是离不开三角函数的,这种方法是把一串序列绕成一个圆,如图所示:

这是我随便从网上下载的图片,简单了解方式即可;第一个位置从3点钟方向开始,把所有的序列逆时针打满一圈,这就是旋转位置编码,论文中有一张图很形象,如图所示:

下面便是上图的公式化表达;

论文中得出这一公式有一个推导,有意思但同时有点长,我把他贴在下面;

这样做有什么优势呢?
Long-term decay


∑
i
=
1
d
/
2
∣
S
i
∣
sum_{i=1}^{d/2}|S_i|
∑i=1d/2∣Si∣在
n
−
m
n-m
n−m上虽然不是单调递减,但是其总体趋势是递减的
Adaption for linear attention
其相对位置不需要学习,不需要训练参数,只需要乘以一个旋转矩阵,类似于绝对编码,但是其实质有相对性;
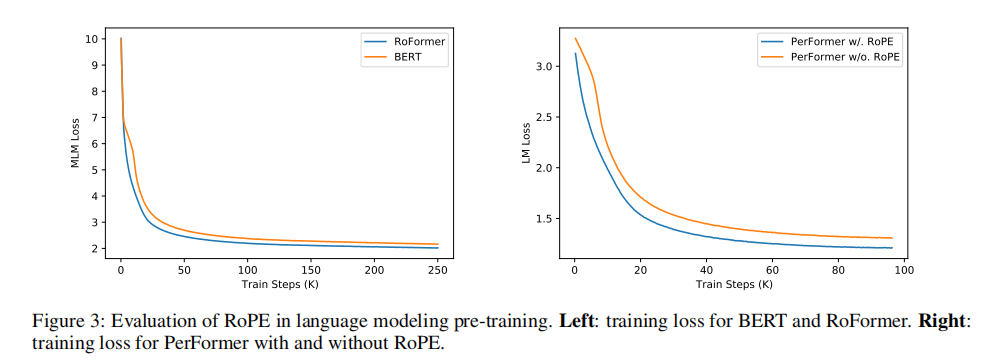
2.5 模型效果
从下图中可以看到RoPE的效果要比Sinusoidal positional encoding要好;
三、过程实现
class RotaryEmbedding(tf.keras.layers.Layer):
def __init__(
self,
max_wavelength=10000,
scaling_factor=1.0,
sequence_axis=1,
feature_axis=-1,
**kwargs
):
super().__init__(**kwargs)
self.max_wavelength = max_wavelength
self.sequence_axis = sequence_axis
self.feature_axis = feature_axis
self.scaling_factor = scaling_factor
self.built = True
def call(self, inputs, start_index=0):
rotary_dim = tf.shape(inputs)[-1]
cos_emb, sin_emb = self._compute_cos_sin_embedding(
inputs, rotary_dim, start_index
)
return self._apply_rotary_pos_emb(inputs, cos_emb, sin_emb)
def _apply_rotary_pos_emb(self, tensor, cos_emb, sin_emb):
x1, x2 = tf.split(tensor, 2, axis=self.feature_axis)
half_rot_tensor = tf.concat((-x2, x1), axis=self.feature_axis)
return (tf.matmul(tensor,cos_emb)) + (tf.matmul(half_rot_tensor, sin_emb))
def _compute_cos_sin_embedding(self, x, rotary_dim, start_index):
freq_range = tf.range(0, rotary_dim, 2, dtype="float32")
freq_range = tf.cast(freq_range, self.compute_dtype)
freq_range = freq_range / tf.cast(
self.scaling_factor, self.compute_dtype
)
inverse_freq = 1.0 / (
self.max_wavelength
** (freq_range / tf.cast(rotary_dim, self.compute_dtype))
)
seq_len = tf.shape(x)[self.sequence_axis]
tensor = tf.range(seq_len, dtype="float32") + start_index
tensor = tf.cast(tensor, dtype=inverse_freq.dtype)
freq = tf.einsum("i, j -> ij", tensor, inverse_freq)
embedding = tf.concat((freq, freq), axis=self.feature_axis)
def get_axis(axis):
return axis if axis > 0 else len(x.shape) + axis
feature_axis = get_axis(self.feature_axis)
sequence_axis = get_axis(self.sequence_axis)
for axis in range(len(x.shape)):
if axis != sequence_axis and axis != feature_axis:
embedding = tf.expand_dims(embedding, axis)
return tf.cos(embedding), tf.sin(embedding)
四、整体总结
中国人牛逼!
原文地址:https://blog.csdn.net/m0_72947390/article/details/134772938
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。
如若转载,请注明出处:http://www.7code.cn/show_37662.html
如若内容造成侵权/违法违规/事实不符,请联系代码007邮箱:suwngjj01@126.com进行投诉反馈,一经查实,立即删除!