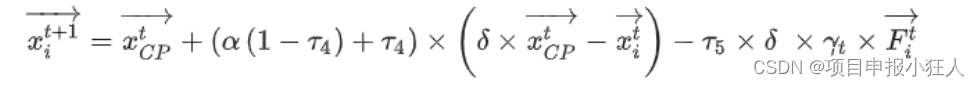算法设计与实现–贪心篇

本文介绍: 贪心算法是一种在每一步选择中都采取当前状态下最优决策的算法，以期望能够通过一系列局部最优的选择达到全局最优。贪心算法的关键是定义好局部最优的选择，并且不回退，即一旦做出了选择，就不能撤销。关键的两步提出贪心策略：观察问题特征，构造贪心选择证明贪心正确：假设最优方案，通过替换证明。

贪心算法

贪心算法是一种在每一步选择中都采取当前状态下最优决策的算法，以期望能够通过一系列局部最优的选择达到全局最优。贪心算法的关键是定义好局部最优的选择，并且不回退，即一旦做出了选择，就不能撤销。

一般来说，贪心算法适用于满足以下两个条件的问题：

最优子结构性质（Op tim al Sub structure）： 问题的最优解包含了其子问题的最优解。这意味着可以通过子问题的最优解来构造原问题的最优解。
贪心选择性质（Gr ee d y Ch o i ce Prope rt y）： 当考虑做某个选择时，贪心算法总是选择当前看起来最优的解，而不考虑其他可能性。这个选择是局部最优的，希望通过这种选择能够达到全局最优。

关键的两步
提出贪心策略：观察问题特征，构造贪心选择
证明贪心正确：假设最优方案，通过替换证明

相关问题

1、部分 背包问题

问题描述

部分背包问题是背包问题的一个变体，与 0-1 背包问题和完全背包问题不同。在部分背包问题中，每个物品可以选择一部分放入背包，而不是必须选择放入或不放入。

以下是部分背包问题的算法思想：

计算单位价值： 对每个物品计算单位价值，单位价值等于物品的价值/物品的重量。

单位价值=物品的价值/物品的重量
按单位价值降序排序： 将所有物品按照单位价值降序排列，这样就可以优先选择单位价值较高的物品。
贪心选择： 从排好序的物品列表中按顺序选择物品放入背包。对于每个物品，可以选择一部分（即部分背包），而不必全部选择。
计算总价值： 根据所选物品计算放入背包的总价值

算法实现

#include &lt;stdio.h&gt;
#include &lt;stdlib.h&gt;

// 物品的结构
struct Item{
	int weight;  // 物品重量 
	int value;   // 物品价值 
}; 

// 1计算单位价值
double computeUnitValue(struct Item item){
	double result = item.value/item.weight;
	return result;
} 

// 2 按单位价值进行降序排序
// 在这个比较函数中，参数的类型为 const void*，
//这是因为这个函数是用于通用排序算法（例如 qsort）的，
//而通用排序算法不关心待排序元素的具体类型
int compare(const void* a,const void* b) {
	// *(struct Item*) 
	// 这是一种类型转换，将通用指针 const void* 转换为具体类型 struct Item*
	 double unitValueA = computeUnitValue(*(struct Item*)a);
	 double unitValueB = computeUnitValue(*(struct Item*)b);
	 
	 if(unitValueA < unitValueB){
	 	return 1;
	 }else if(unitValueA > unitValueB){
	 	return -1;
	 }else{
	 	return 0;
	 }
}

// 3 贪心算法
double fractionalKnapsack(struct Item items[],int n,int vtl) {
	// 跟据单位价值降序排列 
	qsort(items,n,sizeof(struct Item),compare);
	
	// 最大总价值 
	double maxValue = 0.0;  
	
	// 从排好序的物品列表中贪心选择，选择单位价值大的物品
	// 此时的items 是已经是跟据单位价值降序排序的，所以items[0] 是单位价值最大的物品 
	for(int i=0;i<n;i++){
		//  如果背包的容量>=物品的容量，则贪心策略，将整个物品放入背包 
		if(vtl>=items[i].weight){
			maxValue += items[i].value;  //  最大的价值更新 
			vtl -= items[i].weight;		// 背包容量更新 
		}else{ // 如果背包容量没法将整个物品放入，则计算他的单位价值，然后单位价值*剩余背包容量 
			maxValue += computeUnitValue(items[i])*vtl;
			break;
		}
	} 
	
	return maxValue;
}


// 主函数
int main() {
    struct Item items[] = {{10, 60}, {20, 100}, {30, 120}};
    int n = sizeof(items) / sizeof(items[0]);
    int vtl = 50; // 背包容量 

    double maxValue = fractionalKnapsack(items, n, capacity);

    printf("Maximum value that can be obtained = %.2fn", maxValue);

    return 0;
}

2、哈夫曼 编码

哈夫曼编码（Huf fman Cod ing）是一种基于字符出现频率的编码方式，它通过使用较短的比特序列来表示出现频率较高的字符，从而实现对数据的高效压缩。这种编码方式是由大卫·哈夫曼（Dav id A. Huffman）于1952年提出的。

哈夫曼编码的基本思想：

构建哈夫曼树（Huffman Tr ee）：
- 对于需要编码的字符，根据其出现频率构建一个哈夫曼树。
- 频率越高的字符在树中离根越近，频率越低的字符在树中离根越远。（首先选择最小的两个频）
分配编码：
- 遍历哈夫曼树的路径，给每个字符分配一个独一无二的二进制编码。
- 一般来说，向左走表示添加一个0，向右走表示添加一个1。
生成哈夫曼编码表：
- 将每个字符与其对应的二进制编码建立映射关系，形成哈夫曼编码表。

算法实现

#include <stdio.h>
#include <stdlib.h>

// 哈夫曼树节点结构
struct HuffmanNode {
    char data;
    int frequency;
    struct HuffmanNode* left;
    struct HuffmanNode* right;
};

// 字符频率表结构
struct FrequencyTable {
    char data;
    int frequency;
};

// 优先队列中的元素
struct PriorityQueueElement {
    struct HuffmanNode* node;
    struct PriorityQueueElement* next;
};

// 优先队列结构
struct PriorityQueue {
    struct PriorityQueueElement* front;
};

// 初始化优先队列
void initPriorityQueue(struct PriorityQueue* pq) {
    pq->front = NULL;
}

// 插入元素到优先队列
void insertPriorityQueue(struct PriorityQueue* pq, struct HuffmanNode* node) {
    struct PriorityQueueElement* newElement = (struct PriorityQueueElement*)malloc(sizeof(struct PriorityQueueElement));
    newElement->node = node;
    newElement->next = NULL;

    if (pq->front == NULL || node->frequency < pq->front->node->frequency) {
        newElement->next = pq->front;
        pq->front = newElement;
    } else {
        struct PriorityQueueElement* current = pq->front;
        while (current->next != NULL &amp;&amp; current->next->node->frequency <= node->frequency) {
            current = current->next;
        }
        newElement->next = current->next;
        current->next = newElement;
    }
}

// 从优先队列中取出最小元素
struct HuffmanNode* extractMinPriorityQueue(struct PriorityQueue* pq) {
    if (pq->front == NULL) {
        return NULL;
    }

    struct HuffmanNode* minNode = pq->front->node;
    struct PriorityQueueElement* temp = pq->front;
    pq->front = pq->front->next;
    free(temp);

    return minNode;
}

// 构建哈夫曼树
struct HuffmanNode* buildHuffmanTree(struct FrequencyTable frequencies[], int n) {
    struct PriorityQueue pq;
    initPriorityQueue(&amp;pq);

    // 初始化优先队列，每个节点作为一个单独的树
    for (int i = 0; i < n; ++i) {
        struct HuffmanNode* newNode = (struct HuffmanNode*)malloc(sizeof(struct HuffmanNode));
        newNode->data = frequencies[i].data;
        newNode->frequency = frequencies[i].frequency;
        newNode->left = newNode->right = NULL;
        insertPriorityQueue(&amp;pq, newNode);
    }

    // 重复合并节点，直到队列中只剩下一个节点，即哈夫曼树的根
    while (pq.front->next != NULL) {
        struct HuffmanNode* leftChild = extractMinPriorityQueue(&pq);
        struct HuffmanNode* rightChild = extractMinPriorityQueue(&pq);

        struct HuffmanNode* newNode = (struct HuffmanNode*)malloc(sizeof(struct HuffmanNode));
        newNode->data = ''; // 内部节点没有字符数据
        newNode->frequency = leftChild->frequency + rightChild->frequency;
        newNode->left = leftChild;
        newNode->right = rightChild;

        insertPriorityQueue(&pq, newNode);
    }

    // 返回哈夫曼树的根节点
    return extractMinPriorityQueue(&pq);
}

// 生成哈夫曼编码
void generateHuffmanCodes(struct HuffmanNode* root, int code[], int top) {
    if (root->left != NULL) {
        code[top] = 0;
        generateHuffmanCodes(root->left, code, top + 1);
    }

    if (root->right != NULL) {
        code[top] = 1;
        generateHuffmanCodes(root->right, code, top + 1);
    }

    if (root->left == NULL && root->right == NULL) {
        printf("Character: %c, Code: ", root->data);
        for (int i = 0; i < top; ++i) {
            printf("%d", code[i]);
        }
        printf("n");
    }
}

// 主函数
int main() {
    struct FrequencyTable frequencies[] = {{'A', 2}, {'B', 1}, {'C', 1}, {'D', 1},{'E',4}
	};
    int n = sizeof(frequencies) / sizeof(frequencies[0]);

    struct HuffmanNode* root = buildHuffmanTree(frequencies, n);

    int code[100];
    int top = 0;

    printf("Huffman Codes:n");
    generateHuffmanCodes(root, code, top);

    return 0;
}

3、活动选择问题

活动选择问题（Acti vity Sel ection Problem）是一个经典的贪心算法问题，也称为区间调度问题。给定一组活动，每个活动都有一个开始时间和结束时间，目标是选择出最大可能的互不相交的活动子集。

以下是活动选择问题的算法思想：

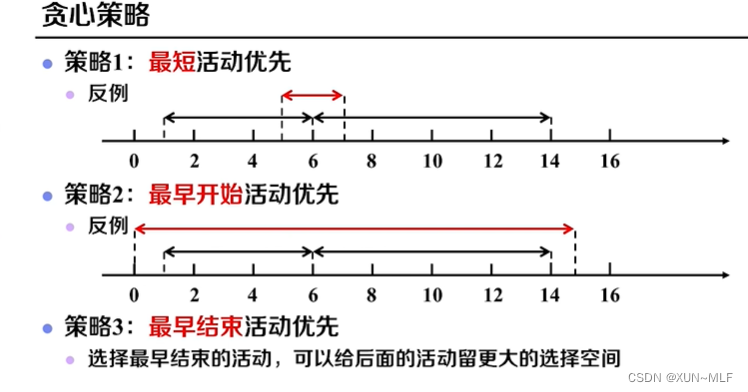
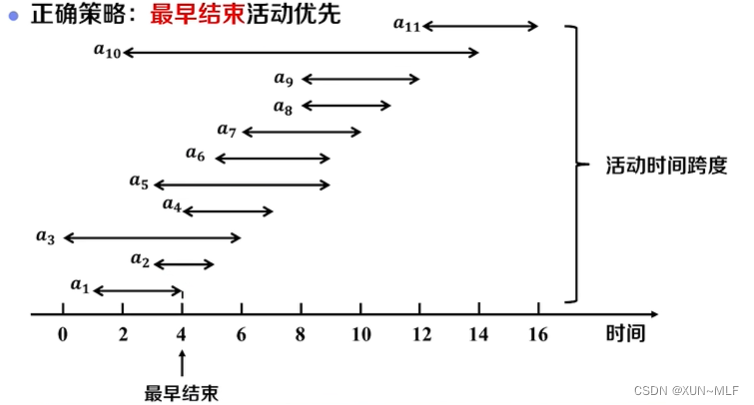
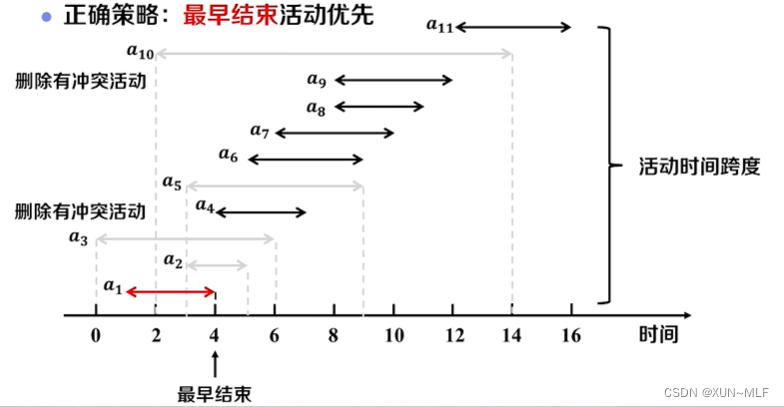
将活动按照结束时间的先后顺序进行排序。
选择第一个活动作为初始活动，并将其加入最终选择的活动子集。
从第二个活动开始，依次判断每个活动是否与已选择的活动相容（即结束时间是否早于下一个活动的开始时间），如果相容，则将该活动加入最终选择的活动子集。
重复步骤3，直到遍历完所有活动。

通过贪心策略，每次选择结束时间最早的活动，可以确保选择的活动子集最大化。因为如果一个活动与已选择的活动相容，那么它一定是结束时间最早的活动，选择它不会影响后续活动的选择。
在这里插入图片描述

在这里插入图片描述

代码实现

该算法的核心就是每次选择结束时间最早的活动

#include <stdio.h>
#include <stdlib.h>

// 活动结构
struct Activity {
    int start;
    int end;
};

// 比较函数，用于按结束时间升序排序
int compare(const void* a, const void* b) {
    return ((struct Activity*)a)->end - ((struct Activity*)b)->end;
}

// 活动选择算法
void activitySelection(struct Activity activities[], int n) {
    // 按结束时间升序排序
    qsort(activities, n, sizeof(struct Activity), compare);

    // 第一个活动总是被选择
    printf("Selected activity: (%d, %d)n", activities[0].start, activities[0].end);

    // 从第二个活动开始选择
    int lastActivity = 0;
    for (int i = 1; i < n; ++i) {
        // 如果活动的开始时间晚于或等于上一个已选择活动的结束时间，选择该活动
        if (activities[i].start >= activities[lastActivity].end) {
            printf("Selected activity: (%d, %d)n", activities[i].start, activities[i].end);
            lastActivity = i;
        }
    }
}

// 主函数
int main() {
    struct Activity activities[] = {{1, 4}, {3, 5}, {0, 6}, {5, 7}, {3, 9}, {5, 9}, {6, 10}, {8, 11}, {8, 12}, {2, 14}, {12, 16}};
    int n = sizeof(activities) / sizeof(activities[0]);

    printf("Activity schedule:n");
    activitySelection(activities, n);

    return 0;
}