Description
The score of an array is defined as the product of its sum and its length.
For example, the score of [1, 2, 3, 4, 5] is (1 + 2 + 3 + 4 + 5) * 5 = 75.
Given a positive integer array nums and an integer k, return the number of non–empty subarrays of nums whose score is strictly less than k.
A subarray is a contiguous sequence of elements within an array.
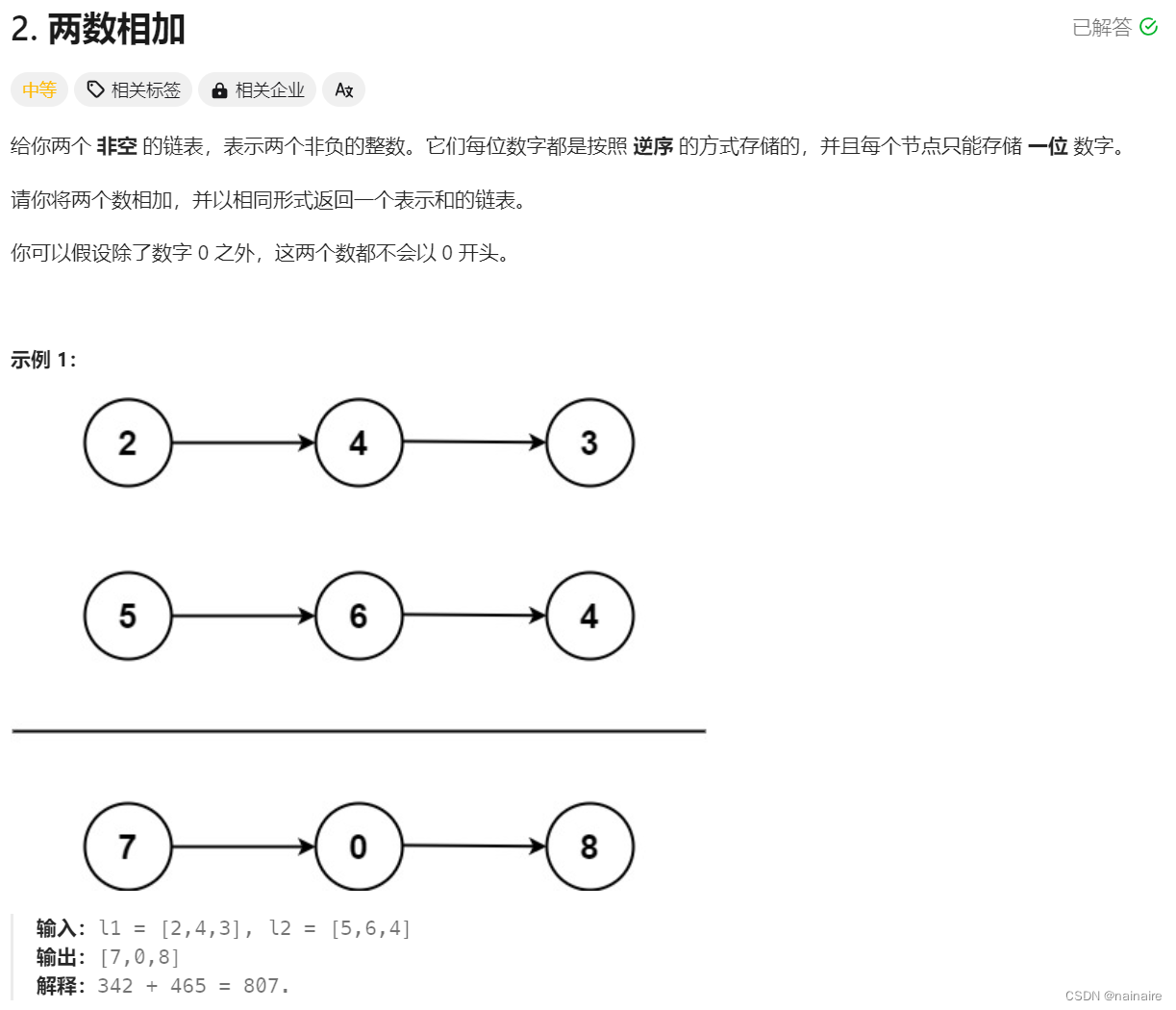
Example 1:
Input: nums = [2,1,4,3,5], k = 10
Output: 6
Explanation:
The 6 subarrays having scores less than 10 are:
- [2] with score 2 * 1 = 2.
- [1] with score 1 * 1 = 1.
- [4] with score 4 * 1 = 4.
- [3] with score 3 * 1 = 3.
- [5] with score 5 * 1 = 5.
- [2,1] with score (2 + 1) * 2 = 6.
Note that subarrays such as [1,4] and [4,3,5] are not considered because their scores are 10 and 36 respectively, while we need scores strictly less than 10.
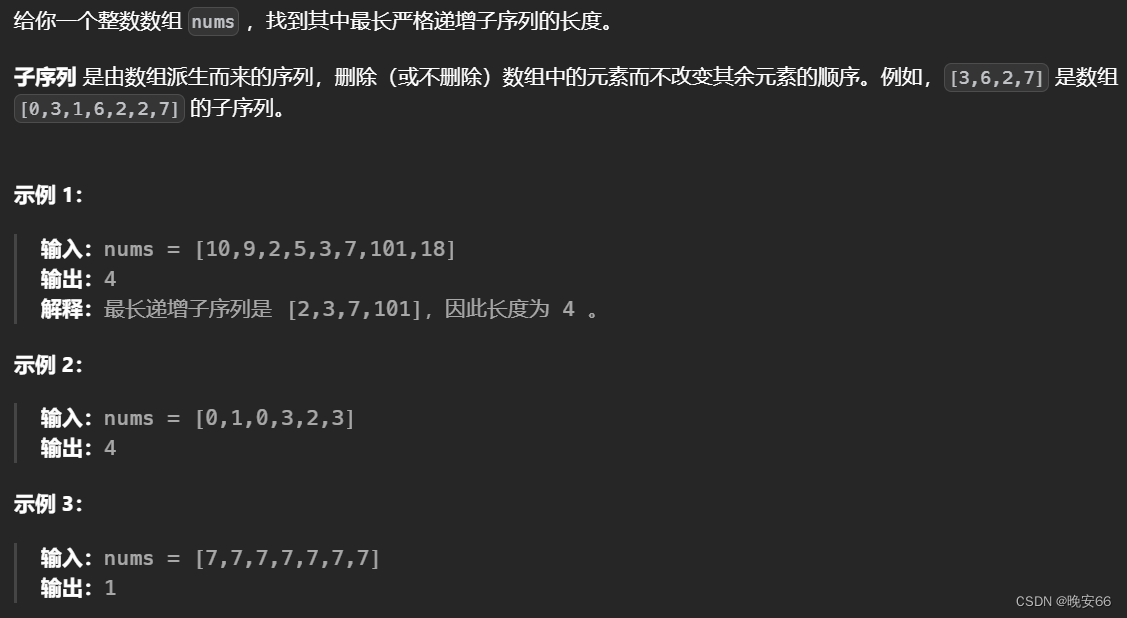
Example 2:
Input: nums = [1,1,1], k = 5
Output: 5
Explanation:
Every subarray except [1,1,1] has a score less than 5.
[1,1,1] has a score (1 + 1 + 1) * 3 = 9, which is greater than 5.
Thus, there are 5 subarrays having scores less than 5.
1 <= nums.length <= 10^5
1 <= nums[i] <= 10^5
1 <= k <= 10^15
Solution
Sliding window, when the score of the subarray is not less than k, shrink the window. Since we need to calculate the number of the subarray, every time we expand the window, calculate the number of subarray with nums[j] as the ending element.
o
(
n
)
o(n)
o(n)
Space complexity:
o
(
1
)
o(1)
o(1)
Code
class Solution:
def countSubarrays(self, nums: List[int], k: int) -> int:
cur_sum, res = 0, 0
i = 0
for j in range(len(nums)):
cur_sum += nums[j]
while cur_sum * (j - i + 1) >= k:
cur_sum -= nums[i]
i += 1
# j - i + 1 is the number of subarray with nums[j] as the ending element
res += j - i + 1
return res
原文地址:https://blog.csdn.net/sinat_41679123/article/details/134623612
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。
如若转载,请注明出处:http://www.7code.cn/show_3917.html
如若内容造成侵权/违法违规/事实不符,请联系代码007邮箱:suwngjj01@126.com进行投诉反馈,一经查实,立即删除!