11. 哈希冲突

上一节提到，通常情况下哈希函数的输入空间远大于输出空间，因此理论上哈希冲突是不可避免的。比如，输入空间为全体整数，输出空间为数组容量大小，则必然有多个整数映射至同一桶索引。

哈希冲突会导致查询结果错误，严重影响哈希表的可用性。为解决该问题，我们可以每当遇到哈希冲突就进行哈希表扩容，直至冲突消失为止。此方法简单粗暴且有效，但效率太低，因为哈希表扩容需要进行大量的数据搬运与哈希值计算。为了提升效率，我们可以采用以下策略。

1. 改良哈希表数据结构，使得哈希表可以在出现哈希冲突时正常工作。
2. 仅在必要时，即当哈希冲突比较严重时，才执行扩容操作。

哈希表的结构改良方法主要包括“链式地址”和“开放寻址”。

11.1 链式地址

在原始哈希表中，每个桶仅能存储一个键值对。链式地址(separate chaining)将单个元素转换为链表，将键值对作为链表节点，将所有发生冲突的键值对都存储在同一链表中。下图展示了一个链式地址哈希表的例子。

基于链式地址实现的哈希表的操作方法发生了以下变化。

• 查询元素：输入 key ，经过哈希函数得到桶索引，即可访问链表头节点，然后遍历链表并对比 key 以查找目标键值对。
• 添加元素：首先通过哈希函数访问链表头节点，然后将节点（键值对）添加到链表中。
• 删除元素：根据哈希函数的结果访问链表头部，接着遍历链表以查找目标节点并将其删除。

链式地址存在以下局限性。

• 占用空间增大，链表包含节点指针，它相比数组更加耗费内存空间。
• 查询效率降低，因为需要线性遍历链表来查找对应元素。

以下代码给出了链式地址哈希表的简单实现，需要注意两点。

• 使用列表（动态数组）代替链表，从而简化代码。在这种设定下，哈希表（数组）包含多个桶，每个桶都是一个列表。
• 以下实现包含哈希表扩容方法。当负载因子超过 2/3 时，我们将哈希表扩容至原先的 2 倍。

  /* 链式地址哈希表 */
  class HashMapChaining {
    private:
      int size;                       // 键值对数量
      int capacity;                   // 哈希表容量
      double loadThres;               // 触发扩容的负载因子阈值
      int extendRatio;                // 扩容倍数
      vector&lt;vector<Pair *&gt;&gt; buckets; // 桶数组
  
    public:
      /* 构造方法 */
      HashMapChaining() : size(0), capacity(4), loadThres(2.0 / 3.0), extendRatio(2) {
          buckets.resize(capacity);
      }
  
      /* 析构方法 */
      ~HashMapChaining() {
          for (auto &amp;bucket : buckets) {
              for (Pair *pair : bucket) {
                  // 释放内存
                  delete pair;
              }
          }
      }
  
      /* 哈希函数 */
      int hashFunc(int key) {
          return key % capacity;
      }
  
      /* 负载因子 */
      double loadFactor() {
          return (double)size / (double)capacity;
      }
  
      /* 查询操作 */
      string get(int key) {
          int index = hashFunc(key);
          // 遍历桶，若找到 key 则返回对应 val
          for (Pair *pair : buckets[index]) {
              if (pair-&gt;key == key) {
                  return pair-&gt;val;
              }
          }
          // 若未找到 key 则返回空字符串
          return "";
      }
  
      /* 添加操作 */
      void put(int key, string val) {
          // 当负载因子超过阈值时，执行扩容
          if (loadFactor() &gt; loadThres) {
              extend();
          }
          int index = hashFunc(key);
          // 遍历桶，若遇到指定 key ，则更新对应 val 并返回
          for (Pair *pair : buckets[index]) {
              if (pair-&gt;key == key) {
                  pair->val = val;
                  return;
              }
          }
          // 若无该 key ，则将键值对添加至尾部
          buckets[index].push_back(new Pair(key, val));
          size++;
      }
  
      /* 删除操作 */
      void remove(int key) {
          int index = hashFunc(key);
          auto &amp;bucket = buckets[index];
          // 遍历桶，从中删除键值对
          for (int i = 0; i < bucket.size(); i++) {
              if (bucket[i]->key == key) {
                  Pair *tmp = bucket[i];
                  bucket.erase(bucket.begin() + i); // 从中删除键值对
                  delete tmp;                       // 释放内存
                  size--;
                  return;
              }
          }
      }
  
      /* 扩容哈希表 */
      void extend() {
          // 暂存原哈希表
          vector<vector<Pair *>> bucketsTmp = buckets;
          // 初始化扩容后的新哈希表
          capacity *= extendRatio;
          buckets.clear();
          buckets.resize(capacity);
          size = 0;
          // 将键值对从原哈希表搬运至新哈希表
          for (auto &amp;bucket : bucketsTmp) {
              for (Pair *pair : bucket) {
                  put(pair->key, pair->val);
                  // 释放内存
                  delete pair;
              }
          }
      }
  
      /* 打印哈希表 */
      void print() {
          for (auto &amp;bucket : buckets) {
              cout << "[";
              for (Pair *pair : bucket) {
                  cout << pair->key << " -> " << pair->val << ", ";
              }
              cout << "]n";
          }
      }
  };
  

  值得注意的是，当链表很长时，查询效率 O(n) 很差。此时可以将链表转换为“AVL 树”或“红黑树”，从而将查询操作的时间复杂度优化至 O(logn) 。

11.2 开放寻址 

开放寻址(open addressing)不引入额外的数据结构，而是通过“多次探测”来处理哈希冲突，探测方式主要包括线性探测、平方探测、多次哈希等。

下面以线性探测为例，介绍开放寻址哈希表的工作机制。

11.2.1 线性探测

线性探测采用固定步长的线性搜索来进行探测，其操作方法与普通哈希表有所不同。

• 插入元素：通过哈希函数计算桶索引，若发现桶内已有元素，则从冲突位置向后线性遍历（步长通常为 1 ），直至找到空桶，将元素插入其中。
• 查找元素：若发现哈希冲突，则使用相同步长向后线性遍历，直到找到对应元素，返回 value 即可；如果遇到空桶，说明目标元素不在哈希表中，返回 None 。

下图展示了开放寻址（线性探测）哈希表的键值对分布。根据此哈希函数，最后两位相同的 key 都会被映射到相同的桶。而通过线性探测，它们被依次存储在该桶以及之下的桶中。

然而，线性探测容易产生“聚集现象”。具体来说，数组中连续被占用的位置越长，这些连续位置发生哈希冲突的可能性越大，从而进一步促使该位置的聚堆生长，形成恶性循环，最终导致增删查改操作效率劣化。

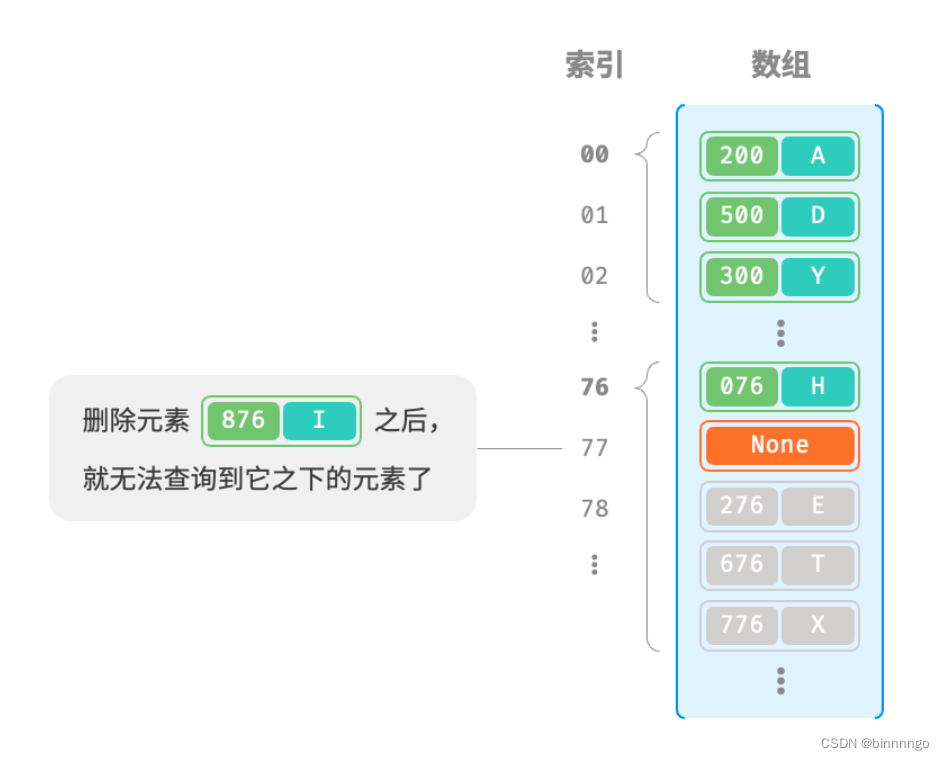
值得注意的是，我们不能在开放寻址哈希表中直接删除元素。这是因为删除元素会在数组内产生一个空桶 None ，而当查询元素时，线性探测到该空桶就会返回，因此在该空桶之下的元素都无法再被访问到，程序可能误判这些元素不存在。

为了解决该问题，我们可以采用懒删除(lazy deletion)机制：它不直接从哈希表中移除元素，而是利用一个常量 TOMBSTONE 来标记这个桶。在该机制下，None 和 TOMBSTONE 都代表空桶，都可以放置键值对。但不同的是，线性探测到 TOMBSTONE 时应该继续遍历，因为其之下可能还存在键值对。

然而，懒删除可能会加速哈希表的性能退化。这是因为每次删除操作都会产生一个删除标记，随着 TOMBSTONE 的增加，搜索时间也会增加，因为线性探测可能需要跳过多个 TOMBSTONE 才能找到目标元素。

为此，考虑在线性探测中记录遇到的首个 TOMBSTONE 的索引，并将搜索到的目标元素与该 TOMBSTONE 交换位置。这样做的好处是当每次查询或添加元素时，元素会被移动至距离理想位置（探测起始点）更近的桶，从而优化查询效率。

以下代码实现了一个包含懒删除的开放寻址（线性探测）哈希表。为了更加充分地使用哈希表的空间，我们将哈希表看作一个“环形数组”，当越过数组尾部时，回到头部继续遍历。

/* 开放寻址哈希表 */
class HashMapOpenAddressing {
  private:
    int size;                             // 键值对数量
    int capacity = 4;                     // 哈希表容量
    const double loadThres = 2.0 / 3.0;     // 触发扩容的负载因子阈值
    const int extendRatio = 2;            // 扩容倍数
    vector<Pair *> buckets;               // 桶数组
    Pair *TOMBSTONE = new Pair(-1, "-1"); // 删除标记

  public:
    /* 构造方法 */
    HashMapOpenAddressing() : size(0), buckets(capacity, nullptr) {
    }

    /* 析构方法 */
    ~HashMapOpenAddressing() {
        for (Pair *pair : buckets) {
            if (pair != nullptr &amp;&amp; pair != TOMBSTONE) {
                delete pair;
            }
        }
        delete TOMBSTONE;
    }

    /* 哈希函数 */
    int hashFunc(int key) {
        return key % capacity;
    }

    /* 负载因子 */
    double loadFactor() {
        return (double)size / capacity;
    }

    /* 搜索 key 对应的桶索引 */
    int findBucket(int key) {
        int index = hashFunc(key);
        int firstTombstone = -1;
        // 线性探测，当遇到空桶时跳出
        while (buckets[index] != nullptr) {
            // 若遇到 key ，返回对应桶索引
            if (buckets[index]->key == key) {
                // 若之前遇到了删除标记，则将键值对移动至该索引
                if (firstTombstone != -1) {
                    buckets[firstTombstone] = buckets[index];
                    buckets[index] = TOMBSTONE;
                    return firstTombstone; // 返回移动后的桶索引
                }
                return index; // 返回桶索引
            }
            // 记录遇到的首个删除标记
            if (firstTombstone == -1 &amp;&amp; buckets[index] == TOMBSTONE) {
                firstTombstone = index;
            }
            // 计算桶索引，越过尾部返回头部
            index = (index + 1) % capacity;
        }
        // 若 key 不存在，则返回添加点的索引
        return firstTombstone == -1 ? index : firstTombstone;
    }

    /* 查询操作 */
    string get(int key) {
        // 搜索 key 对应的桶索引
        int index = findBucket(key);
        // 若找到键值对，则返回对应 val
        if (buckets[index] != nullptr &amp;&amp; buckets[index] != TOMBSTONE) {
            return buckets[index]->val;
        }
        // 若键值对不存在，则返回空字符串
        return "";
    }

    /* 添加操作 */
    void put(int key, string val) {
        // 当负载因子超过阈值时，执行扩容
        if (loadFactor() > loadThres) {
            extend();
        }
        // 搜索 key 对应的桶索引
        int index = findBucket(key);
        // 若找到键值对，则覆盖 val 并返回
        if (buckets[index] != nullptr &amp;&amp; buckets[index] != TOMBSTONE) {
            buckets[index]->val = val;
            return;
        }
        // 若键值对不存在，则添加该键值对
        buckets[index] = new Pair(key, val);
        size++;
    }

    /* 删除操作 */
    void remove(int key) {
        // 搜索 key 对应的桶索引
        int index = findBucket(key);
        // 若找到键值对，则用删除标记覆盖它
        if (buckets[index] != nullptr &amp;& buckets[index] != TOMBSTONE) {
            delete buckets[index];
            buckets[index] = TOMBSTONE;
            size--;
        }
    }

    /* 扩容哈希表 */
    void extend() {
        // 暂存原哈希表
        vector<Pair *> bucketsTmp = buckets;
        // 初始化扩容后的新哈希表
        capacity *= extendRatio;
        buckets = vector<Pair *>(capacity, nullptr);
        size = 0;
        // 将键值对从原哈希表搬运至新哈希表
        for (Pair *pair : bucketsTmp) {
            if (pair != nullptr && pair != TOMBSTONE) {
                put(pair->key, pair->val);
                delete pair;
            }
        }
    }

    /* 打印哈希表 */
    void print() {
        for (Pair *pair : buckets) {
            if (pair == nullptr) {
                cout << "nullptr" << endl;
            } else if (pair == TOMBSTONE) {
                cout << "TOMBSTONE" << endl;
            } else {
                cout << pair->key << " -> " << pair->val << endl;
            }
        }
    }
};

11.2.2 平方探测

平方探测与线性探测类似，都是开放寻址的常见策略之一。当发生冲突时，平方探测不是简单地跳过一个固定的步数，而是跳过“探测次数的平方”的步数，即 1,4,9,… 步。

平方探测主要具有以下优势。

• 平方探测通过跳过平方的距离，试图缓解线性探测的聚集效应。
• 平方探测会跳过更大的距离来寻找空位置，有助于数据分布得更加均匀。

然而，平方探测也并不是完美的。

• 仍然存在聚集现象，即某些位置比其他位置更容易被占用。
• 由于平方的增长，平方探测可能不会探测整个哈希表，这意味着即使哈希表中有空桶，平方探测也可能无法访问到它。

11.2.3 多次哈希

顾名思义，多次哈希方法使用多个哈希函数 f1(x)、f2(x)、f3(x)、… 进行探测。

• 插入元素：若哈希函数 f1(x) 出现冲突，则尝试 f2(x) ，以此类推，直到找到空桶后插入元素。
• 查找元素：在相同的哈希函数顺序下进行查找，直到找到目标元素时返回；若遇到空桶或已尝试所有哈希函数，说明哈希表中不存在该元素，则返回 None 。

与线性探测相比，多次哈希方法不易产生聚集，但多个哈希函数会带来额外的计算量。

11.3 编程语言的选择 

各个编程语言采取了不同的哈希表实现策略，以下举几个例子。

• Python 采用开放寻址。字典 dict 使用伪随机数进行探测。
• Java 采用链式地址。自 JDK 1.8 以来，当 HashMap 内数组长度达到 64 且链表长度达到 8 时，链表会转换为红黑树以提升查找性能。
• Go 采用链式地址。Go 规定每个桶最多存储 8 个键值对，超出容量则连接一个溢出桶。当溢出桶过多时，会执行一次特殊的等量扩容操作，以确保性能。

代码007普通

打赏 收藏 海报 链接