机器学习（1）机器学习类型和机器学习的主要概念

本文介绍: 摆烂才是王道

0.前提

深度学习（Dee p Le ar in g）是机器学习（Ma ch in e Lea rn in g）领域中的一个新的研究方向，在如今的时代研究深度学习的大模型是十分热门的。我不知道有多少人有关注到最近openai的事件啊，说个比较让我惊讶的事情，一直在支持我做一些实验的老师今年在ICCV的A区发文章，直接给我看傻了，平常经常看到老师骑着电车在学校里面跑。既然深度学习是机器学习的一个子集，那想要入门深度学习，学习机器学习那就很有必要了。这篇文章也是为了在未来更好的解剖了解我的智能小车。

1.机器学习的类型

机器学习包含监督学习、无监督学习、强化学习等。

1.监督学习

·监督学习是指利用有标签数据进行训练从而得到预测模型的学习任务。换句话说就是训练的数据有标签，输入数据x 预测 y。

·监督学习算法主要分两类：离散的，那就是分类算法（classification）；连续的，那就是回归算法（reg res s ion）。

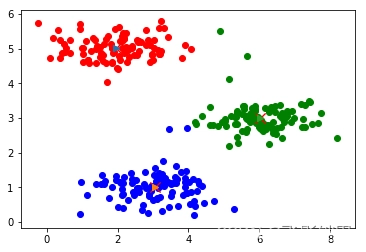
1.分类算法

分类指基于预测模型，推理出离散的的输出值：0或1。

2.回归算法

回归指基于预测模型对未知的输出值推测出一个连续值得结果。

2.无监督学习

·无监督学习里的数据只有输入属性，没有标签。

·无监督学习算法是基于一种“物以类聚”的思想：聚类算法和关联算法

3.强化学习

强化学习用于描述和解决智能体在环境的交互过程中通过学习策略以达成回报最大化或实现特定目标的问题。这有点类似下棋时的博弈论。

2.机器学习的主要概念

机学习的方法由模型、损失函数、优化算法、模型评估指标等几个要素构成。

1.模型

机器学习要先考虑使用的模型。模型类别大致分为概率模型和非概率模型。

1.概率模型

·在监督学习中：概率模型表示为P(y|x)。x是输入，y是输出。

·在无监督学习中：概率模型表示为P(z|x)。x是输入，z是输出。

·决策树、朴素贝叶斯、隐马尔科夫模型、高斯混合模型属于概率模型

2.非概率模型

·在监督学习中：非概率模型表示为y=f(x)。x是输入，y是输出。

·在非监督学习中：非概率模型表示为z=f(x)。x是输入，z是输出。

·感知机、支持向量机、KNN、Ad aBo os t、K-means以及神经网络均属于非概率模型。

非概率模型又可按函数线性性分为线性模型和非线性模型。

2.损失 函数

在机器学习中常见的损失函数有4种。有没有很熟悉的感觉？

损失函数数值越小，模型性能越好。平均损失被称为经验风险。经验风险最小化，得出全局损失函数最优解问题：

$_{f}^{min}textrm{}frac{1}{N}sum_{n=1}^{N}L(y_{a},f(x_{n}))$

当样本数量够大时，根据大数定理（既伯努利大数定理，当进行大量实验时，事件的频率趋近于概率），经验风险会近似于模型的期待风险，此时经验风险最小化，有较好的学习效果。但当样本数量不够时，利用经验风险最小化就会“过拟合”，在原基础上加入控制模型复杂度的正则项：

$_{f}^{min}textrm{}frac{1}{N}sum_{n=1}^{N}L(y_{a},f(x_{n}))+lambda J (f)$

J(f)表示对模型复杂度的惩罚。模型越复杂，J(f)越大；模型越简单，J(f)越小。 $lambda$ 是正则化系数，是正常数，用于平衡经验风险和模型复杂度。结构风险小的模型在经验风险和模型复杂度都小时，训练数据和测试数据有较好的拟合。

3.优化算法

算法指模型学习中的具体计算方法。基于参数模型参数模型构建的我统计学习问题为最优化问题，有显式的解析解。优化方法有梯度下降法、牛顿法、拟牛顿法、ADAM等。

4.模型评估

损失函数给定，基于模型训练数据的误差和测试数据的误差作为模型评估的标准。

测试误差的具体定义： $E_{test}=frac{1}{N'}sum_{n=1}^{N'}L(y_{n},widehat{f}(x_{n}))$

N’为测试数据数量，L( $y_{n},widehat{f}(x_{n})$ )是损失函数， $y_{n}$ 代表真实标签， $widehat{f}(x_{n})$ 代表预测标签。若模型学习的效果好，训练误差和测试误差接近一致。

3.机器学习的学习基础

1.高数-导数

高数课本中对导数的定义：设函数 $y=f(x)$ 在点 $x_{0}$ 的某个领域内有定义，当自变量 $x$ 在 $x_{0}$ 处取得增量 $Delta x$ （点 $x_{0}$ + $Delta x$ 仍在该领域内）时，相应地，因变量取得增量 $Delta y$ = $f(x_{0}+Delta x)-f(x_{0})$ ;如果 $Delta y$ 与 $Delta x$ 之比当 $Delta x$ $rightarrow$ 0时的极限存在，那函数 $y=f(x)$ 在 $x_{0}$ 处可导，称该极限为函数 $y=f(x)$ 在 $x_{0}$ 处的导数—— $f'(x_{0})=_{Delta xrightarrow 0}^{lim}frac{Delta y}{Delta x}=_{Delta x}^{lim}frac{f(x_{0}+Delta x)-f(x_{0})}{Delta x}$