机器学习的复习笔记4-岭回归与多项式回归

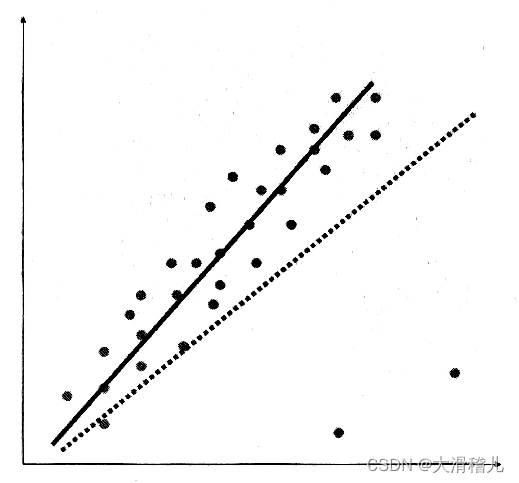
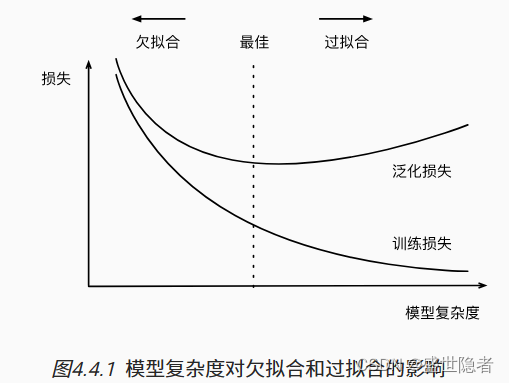
本文介绍: 在实际应用中，可以根据实际情况选择适当的多项式阶数，以达到较好的拟合效果。如图，若为满足所有点的拟合（虚线），表面上看R2值小，但为了右下角两个噪声点严重偏离了大部分点群，这是得不偿失的。其中，ai 是多项式的系数，x1、x2、…、xn 是自变量，y 是因变量。确定多项式的阶数（de g r ee）：多项式的阶数决定了拟合函数的复杂程度。在简单的线性回归中，一味追求平方误差最小化，R2值尽可能大，可能会受到噪声的严重干扰。分析结果：根据拟合的多项式，分析自变量与因变量之间的关系，以及多项式系数对应的含义。

一、岭回归

在简单的线性回归中，一味追求平方误差最小化，R2值尽可能大，可能会受到噪声的严重干扰。噪声，即偶发的错误的值。

如图，若为满足所有点的拟合（虚线），表面上看R2值小，但为了右下角两个噪声点严重偏离了大部分点群，这是得不偿失的。因此设置阈值来过滤少数噪声点的影响，反而会使拟合效果更加合理。而增加阈值的回归，被称为“岭回归”。

from sklearn import linear_model
ridge_regressor=linear_model.Ridge(alpha=100,fit_intercept=True,max_iter=10000)

alpha即为复杂度控制器，值为非负整数，值为0时，等同于使用最小二乘法的普通线性回归。如要屏蔽噪声值，则需加大该值。

二、多项式回归

多项式回归是一种回归分析方法，它通过拟合一个多项式函数来描述自变量与因变量之间的关系。在多项式回归中，自变量和因变量可以是连续变量或离散变量。

from sklearn.preprocessing import PolynomialFeatures

#设置多项式的次幂的初始值
ploynomial=PolynomialFeatures(degree=3)

#多项式形式的输入
X_train_transformed=ploynomial.fit_transform(X_train)

#拟合
poly_linear_model=linear_model.LinearRegression()
poly_linear_model.fit(X_train_transformed,y_train)

多项式回归的主要步骤如下：

确定多项式的阶数（de g ree）：多项式的阶数决定了拟合函数的复杂程度。阶数越高，拟合函数越复杂，但过高的阶数可能导致过拟合。
收集数据：收集与自变量和因变量相关的数据，这些数据通常呈现线性或非线性关系。
拟合多项式：利用数据集拟合一个多项式函数，该函数可以表示为：y = a0 + a1×1 + a2×2 + … + anxn。其中，ai 是多项式的系数，x1、x2、…、xn 是自变量，y 是因变量。
分析结果：根据拟合的多项式，分析自变量与因变量之间的关系，以及多项式系数对应的含义。
评估模型：使用拟合的多项式进行预测，并评估模型的预测性能。过高的阶数可能导致过拟合，因此需要权衡模型的复杂程度与预测性能。