定义
Sampson误差是复杂性介于代数误差和几何误差之间，但非常近似于几何误差的一种误差。
应用
SLAM对极几何中使用到SD来筛选内点：
1.随机采样8对匹配点
2.8点法求解基础矩阵 ；
3.奇异值约束获取基础矩阵F；
4.计算误差，并统计内点个数；
内点判断标准—一阶几何误差(first–order geometric error)，又名辛普森距离(Sampson distance）：令 
则该对应点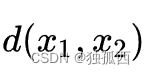
的辛普森距离为为：
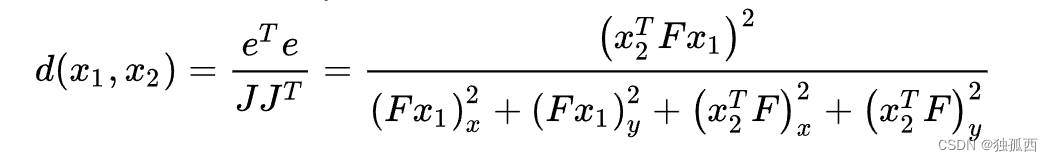
内点的判断标准：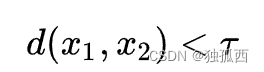 
5.重复上述过程，选择内点数最多的结果；
6.对所有内点执行2,3，重新计算 .
扩展
有一篇论文对SD进行了改进并用在VIO系统中的视觉残差计算上：Sampson Distance: A New Approach to Improving VisualInertial Odometry’s Accuracy。在sampson误差( SD )的基础上提出了一种新的方案来描述视觉惯性里程计( VIO )的视觉特征残差。与基于几何约束条件的视觉里程计( VO )的SD不同，所提出的SD是基于透视投影约束的。这篇论文从理论上证明了所提出的SD保留了VO文献中早期SD准则的良好性质，并且它比现有的VIO方法中流行的转移距离( TD )更准确地表示了视觉特征残差。
原文地址:https://blog.csdn.net/weixin_46190814/article/details/134794312
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。
如若转载，请注明出处：http://www.7code.cn/show_41444.html
如若内容造成侵权/违法违规/事实不符，请联系代码007邮箱：suwngjj01@126.com进行投诉反馈，一经查实，立即删除！
![[软件工具]文档页数统计工具软件pdf统计页数word统计页数ppt统计页数图文打印店快速报价工具](https://img-blog.csdnimg.cn/direct/09dfbaff3e9a47a9a551dd65fef5d482.jpeg)