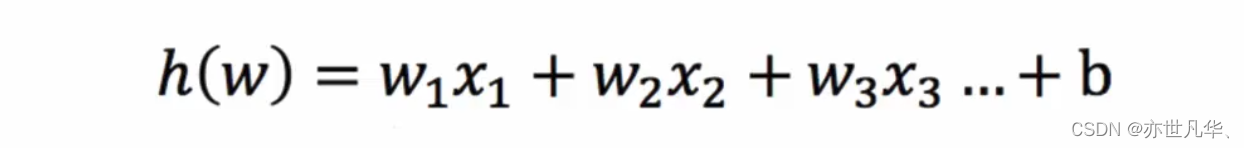机器学习——logistic回归

本文介绍: 在之前实验接触到的机器学习算法都是的目的都是对数据集进行分类，即预测得到的结果是数据样本所属的类别，预测输出结果是离散的集合，比如{‘是’，‘不是’}。这次实验学习的是回归模型，与分类模型不同的是，回归模型预测得到的是一个连续的数值，比如预测房价、温度等得到的值都是连续值。logistic 回归就是一种回归模型，但是logistic回归得到的预测结果是分类，它虽然在中间过程是回归，但使用它的目的和它预测的结果是分类。这次实验学习的就是使用 logistic回归执行分类任务。

在之前实验接触到的机器学习算法都是的目的都是对数据集进行分类，即预测得到的结果是数据样本所属的类别，预测输出结果是离散的集合，比如{‘是’，‘不是’}。这次实验学习的是回归模型，与分类模型不同的是，回归模型预测得到的是一个连续的数值，比如预测房价、温度等得到的值都是连续值。log i st ic回归就是一种回归模型，但是log i st ic回归得到的预测结果是分类，它虽然在中间过程是回归，但使用它的目的和它预测的结果是分类。这次实验学习的就是使用 logist ic回归执行分类任务。

一、线性 模型与回归

本次实验学习的logist ic回归是一种线性回归模型，线性回归的一般形式为：

$f(x)=w_1x_1+w_2x_2+...+w_dx_d+b$

其中 $x=(x_1, x_2, ..., x_d)$ 是数据集样本的d个属性的取值， $x_i$ 即样本 x在第i个属性上的取值。b为偏置，对应回归直线的截距。

上述的式子也可以用向量形式表示：

$f(x)=w^Tx+b$

其中向量 $w=(w_1, w_2, ..., w_d)$ 是样本各个特征取值的权重值，也是logist ic回归需要学习的参数。其实实际相乘时应该是 $xw^T$ （矩阵相乘）。

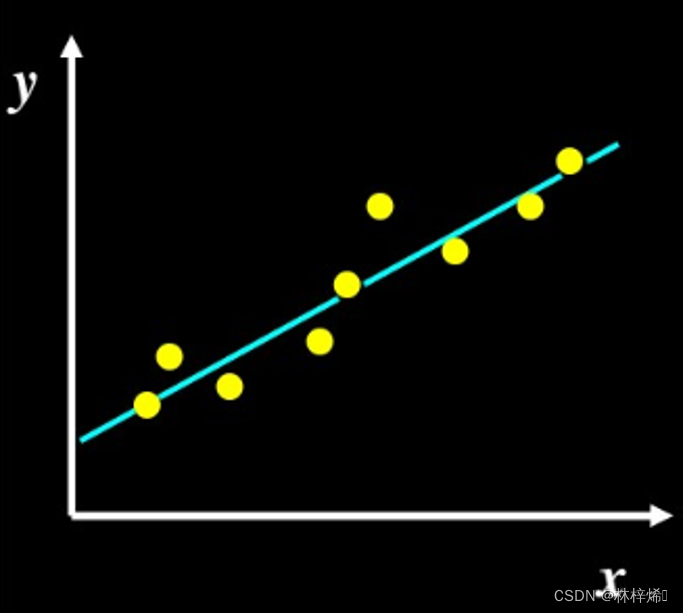
如上图就是一个简单的线性回归模型，这个模型只有一个自变量 x，是一元的线性回归，上图的散点对应数据集中的样本，直线对应训练得到的线性模型，进行预测时根据线性模型将输入转化为对应的输出，输出对应上图直线上的某个点的y值。

线性回归的目的是学习一个线性模型以尽可能准确地预测实值输出标记，也就是要训练得到一个最佳的线性回归模型 $f(x)=wx_i+b$ ，使得每个样本预测结果 $f(x_i)$ 与 $y_i$ 的差距尽可能的小。

在深度学习中我们也有接触到线性回归模型，在深度学习中线性回归模型训练使用的方法是梯度下降法，即计算预测值与实际值之间的损失（损失由损失函数计算得到），然后计算梯度（损失函数对权重和偏置的导数），梯度方向就是函数变化最快的方向，将参数减去梯度再乘上学习率（步长）就能让参数往下降最快的方向更新，最终得到一个最佳的线性回归模型。

logist ic与深度学习中的线性回归模型很类似，lo gist ic是首先计算极大似然函数的梯度，然后使用梯度上升法来训练模型，梯度上升法实际上与梯度下降法是一样的。

二、基于 lo gist ic回归和Sigm o id 函数的分类

线性回归是用来预测一个连续值的，如果数据集的标签是类别（一组离散值）的话，那么线性回归就很难训练出一条拟合数据的直线，因为数据集只包含几种标签值，彼此之间相差很大，而且有很多数据都是同一个标签值，对这样的数据集进行拟合得到的结果是非常差的。要想让线性回归模型拟合这样的数据，就要让线性回归模型输出与分类标签联系起来，让它的输出值转变为分类标签，而不是一个连续值，一种可行的方法就是使用单位阶跃函数。

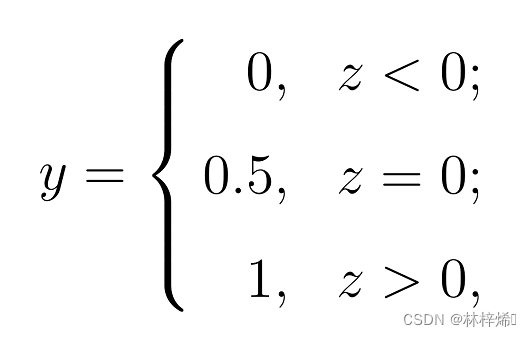
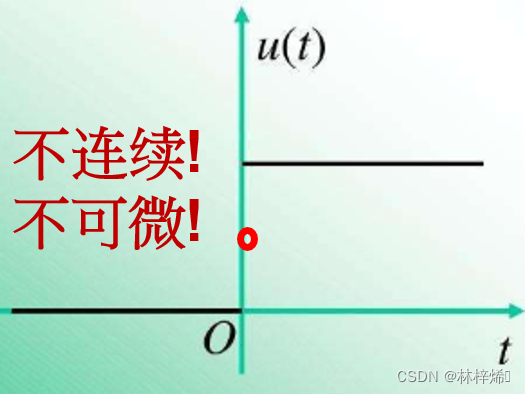
上图的函数将大于0的输出都映射到1，小于0的输出映射到0，只是一个变化非常剧烈的函数，函数在间断点上是直接从0跳跃到1，这样的函数是不连续的，也就导致在这个跳跃点函数是不可微的，因此这个跳跃点是很难处理的。因此我们需要寻找一个更加合适的函数来映射输出。

lo gist ic回归模型使用的函数是Sigm o id函数，这个函数的定义如下：

$y=frac{1}{1+e^{-z}}$

其中z是线性模型预测的输出。

函数图形如下

这个函数相比跃迁函数变化就很平缓了，而且是一个单调可微的函数。虽然在刻度比较小的情况下看着变化有点过于缓慢了，但是如果刻度足够大，那么Sigm o id函数看起来就很接近一个阶跃函数了。如下图所示。

lo gistic回归得到的结果就是线性模型输出经过Sigm oi的函数映射得到的值，这个值处于0-1的区间内，再得到结果后将大于0.5的分类为1，将结果小于0.5的分类为0就能完成对数据集的分类任务了。

三、最优化算法

在回归模型 $f(x)=w^Tx+b$ 中，x是已知的样本，模型训练的目的就是寻找最佳的参数 w和b使得分类器尽可能的精确，要寻找最佳参数，就需要使用最优化算法更新模型参数。

1. 最大 似然 估计

lo gis ti c回归使用的是最大似然估计来寻找最佳的参数。

最大似然估计适用于估计已知分布类型的模型的参数，设 $X_1, X_2, ..., X_n$ 是数据集中的样本，则 $X_1, X_2, ..., X_n$ 有联合分布为 $f(x_1, theta)f(x_2, theta) cdot cdot cdot f(x_n, theta)$ ，其中 $f(x_i, theta)$ 是总体 $X_i$ 的分布， $theta$ 是未知的分布参数（在lo gis ti c回归中对应参数w和b），样本 $X_i$ 的分布律（离散型）我们是已知的，则可以构造一个似然函数

$L(theta)=f(X_1, theta)f(X_2, theta)cdotcdotcdot f(X_n, theta)$

$L(theta)$ 表示由参数 $theta$ 产生样本 $X_1, X_2, ..., X_n$ 的”可能性“大小，若将样本观测看成已经得到的”结果“， $theta$ 则是产生这个”结果“的“原因”，那么要估计一个合理的 $theta$ 值就应该使这个”可能性“（以 $L(theta)$ 度量）达到最大值。

为了简化计算，我们通常会将似然函数取对数，这样就能将概率乘法转换为加法。得到

$lnL(theta)=sum_{i=1}^m lnP(y_i|x_i;theta)$

其中 $y_i$ 是样本的类别， $P(y_i|x_i;theta)$ 是样本的分布律。

在lo gis ti c回归中参数 $theta$ 是w和b，因此可以将上式写作

$lnL(w,b)=sum_{i=1}^m lnP(y_i|x_i;w,b)$

上式中P(y _i|x_i;w,b)该如何得到呢？logisti c回归解决的是二分类问题，样本的标签只有0和1，也就是样本服从伯努利分布，X的分布律为 $P(X=k)=p^k(1-p)^{1-k}, k=0,1$ ，k 对应样本的类别标签 $y_i$ ，现在需要求的就是p，p是事件出现的概率，那么我们就可以将样本为正例的概率设为p，则样本为负例的概率为1-p。将分布律代入上式就能得到

$lnL(w, b)=sum_{i=1}^{m}ln p^{y_{i}}(1-p)^{1-y_i}$

再简化得到

$lnL(w, b)=sum_{i=1}^{m}y_iln p+(1-y_i)ln(1-p)$

我们知道logisti c回归输出的结果是线性回归模型输出结果经过Sigmoid函数映射得到的，对Sigmoid函数进行简单的变换就能得到：

$lnfrac{y}{1-y}=z$

而z是线性模型预测的输出， $z=w^T+b$ ，代入上式得到：

$lnfrac{y}{1-y}=w^Tx+b$

将y看作是样本属于正例的概率，1-y则是样本属于负例的概率，那么 $lnfrac{y}{1-y}$ 就是样本作为正例的概率相对样本作为负例的概率的对数，也就是logisti c回归模型输出的是样本属于正例的相对可能性，即

$lnfrac{y}{1-y}=lnfrac{P(y=1|x)}{P(y=0|x)}=w^Tx+b$

而 $y=frac{1}{1+e^{-z}}$ ，则

$P(y=1|x)=frac{1}{1+e^{-(w^Tx+b)}}$

$P(y=0|x)=frac{e^{-(w^Tx+b)}}{1+e^{-(w^Tx+b)}}$

也可以写作：

$P(y=1|x)=frac{e^{w^Tx+b}}{1+e^{w^Tx+b}}$

$P(y=0|x)=frac{1}{1+e^{w^Tx+b}}$

2. 梯度上升法

本次实验我们使用的最优化算法是梯度上升法。梯度上升法的基本思想就是是：要找到某函数的最大值，最好的方法是沿着该函数的梯度方向探寻，要求函数的梯度就要对函数求导。

因此我们要求最佳的参数w、b，就要使用梯度上升法找到似然函数的最大值，使其达到最大值的参数w、b就是我们要求的最佳的参数。

根据下式

$lnL(w, b)=sum_{i=1}^{m}y_iln p+(1-y_i)ln(1-p)$

$p=P(y=1|x)=frac{e^{w^Tx+b}}{1+e^{w^Tx+b}}$

$z=w^Tx+b$

似然函数对参数w求偏导可以使用链式法则 $frac{partial lnL(w,b)}{partial w}=frac{partial lnL(w,b)}{partial p}*frac{partial p}{partial z}*frac{partial z}{partial w}$ 进行求导，得到

$frac{partial lnL(w,b)}{partial w}=sum_{i=1}^mfrac{y_i}{p}frac{e^z}{(1+e^z)^2}x-frac{1-y_i}{1-p}frac{e^z}{(1+e^z)^2}x$

$=sum_{i=1}^mfrac{e^z}{1+e^z}(frac{y_i-p}{p(1-p)})x$

$=sum_{i=1}^mfrac{e^z}{1+e^z}frac{y_i-p}{frac{e^z}{1+e^z}}x$

$=sum_{i=1}^m(y_i-p)x$

其中 $p=frac{e^{w^Tx+b}}{1+e^{w^Tx+b}}=frac{1}{1+e^{-(w^Tx+b)}}$ ，是线性模型输出经过Sigmoid映射得到的值。

3. 训练算法：梯度上升

梯度上升法的伪代码如下，

1. 每个回归系数初始化为1

2. 重复执行R次（迭代轮数）：

2.1. 计算整个数据集的梯度grad

2.2. 使用lr（学习率） * grad 更新模型参数

3. 返回模型参数

对应代码：

# 梯度上升法，梯度是极大似然函数的梯度，num_epochs：迭代次数
def gradAscent(dataSet, classLabels, num_epochs=500):
    n = dataSet.shape[1]
    # 学习率
    lr = 0.001
    # 初始化权重值全为1
    weights = torch.ones((n, 1))
    # 迭代num_epochs次
    for k in range(num_epochs):
        # 计算线性模型预测值经过Sigmoid函数的映射得到逻辑回归的输出
        y_hat = torch.sigmoid(torch.matmul(dataSet, weights))
        # classLabels和y_hat都是列向量，dataSet要与它们相乘必须转置
        # 计算(yi - p)*x
        maxLikeli = torch.matmul(dataSet.T, (classLabels - y_hat))
        weights += lr * maxLikeli
    return weights

上面代码中的数据集dataSet和类别标签classLabels都是用torch.tensor 存储的，因为深度学习中用tensor 比较多，我比较喜欢用tensor。

先使用一个简单的数据集训练，看看分类结果如何。

部分数据集如下：

-0.017612 14.053064 0

-1.395634 4.662541 1

-0.752157 6.538620 0

-1.322371 7.152853 0

0.423363 11.054677 0

0.406704 7.067335 1

0.667394 12.741452 0

-2.460150 6.866805 1

0.569411 9.548755 0

-0.026632 10.427743 0

这个简单的数据集只包含两个特征值，样本的类别标签包含两种0和1 。

读取该数据集：

def loadDataSet():
    # 数据集
    dataSet = []
    # 类别标签
    classLabels = []
    # 打开文件
    fp = open('testSet.csv')
    for line in fp.readlines():
        # 以空白字符分割数据
        lineSplit = line.strip().split()
        # 1是偏置，将其设为1的话训练出来偏置的权重就是偏置了
        # 将两个特征添加进数据集中
        dataSet.append([1., float(lineSplit[0]), float(lineSplit[1])])
        # 将类别标签添加进classLabels
        classLabels.append(int(lineSplit[2]))
    # 返回数据集和类别标签（类别标签需要将形状转为（n，1））
    return torch.tensor(dataSet), torch.tensor(classLabels).reshape((-1, 1))

上述代码中将为数据集中添加一个特征X0，这个实际是偏置b，在训练时，也会更新它的权重值，最终训练出最佳的b的权重值w0，b*w0就是偏置了，为了简化计算，将其设为1，这样最终训练出的b的权重就直接是偏置了。

Sigmoid函数我直接使用的torch中的sigmoid函数，在深度学习中sigmoid可以作为一个激活函数。因此不需要再自己定义一个。

现在就可以直接开始训练了，我们直接使用默认的迭代次数500进行训练观察结果。

训练：

dataSet, classLabels = loadDataSet()
weights = gradAscent(dataSet, classLabels)

训练结果：

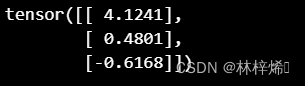
上图中第一个权重是偏置，剩下两个分别是第一、第二个特征的权重。

因为数据集并不是预先给定一个线性回归模型生成的，我们不知道它的实际的参数w、b，所以只从权重上是看不出来训练结果到底好不好的。我们可以将计算错误率来衡量这个模型的好坏，或者我们也可以画图观察。

4. 绘制决策边界

由于我们的数据集只有两个特征，可以将两个特征分别作为x轴和y轴，根据各个样本的两个特征的取值在图中绘制散点图，然后再根据训练得到的权重值和偏置值绘制直线，观察训练得到的直线能否将两种类别的数据集很好的区分开。

对应代码如下：

def plotPredcLine(weights, dataSet, classLabels):
    # 连接特征矩阵和类别标签，便于切片取各类别样本，dim=1是指在维度1（列）连接
    dataMat = torch.cat((dataSet, classLabels), dim=1)
    # 获取dataMat中最后一列（类别）为1的所有样本的第2、3个特征
    # 将两个特征绘制在图形中，两个特征分别作为x，y轴，需要将得到的tensor转置成2xn的矩阵，每行对应一个特征的取值
    class1Cords = dataMat[dataMat[:, -1] == 1][:, 1 : -1].T.tolist()
    # 类别为0
    class2Cords = dataMat[dataMat[:, -1] == 0][:, 1 : -1].T.tolist()
    # 绘制训练得到的直线
    lineX = np.arange(-4, 4, 0.1) # x取一个范围内的连续值（实际是间隔为0.1的离散值）
    lineY = (-weights[0] - weights[1] * lineX) / weights[2]
    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.plot(lineX, lineY)
    ax.scatter(class1Cords[0], class1Cords[1], s=30, c='red', marker='s')
    ax.scatter(class2Cords[0], class2Cords[1], s=30, c='green')

上述代码将数据集和类别标签连接在一起，然后就能直接根据连接矩阵最后一列的值（类别标签）分出两种类别的样本，而样本中第一个数据是偏置是不需要的，最后一个数据类别标签也是不需要的，我们切片只取1到2列的数据，这两个数据就是第一个和第二个特征。

上面绘制的直线其实并不是真正的线性回归模型，因为它的自变量是X1，因变量是X2，并不是线性模型的 $f(x)=w^Tx+b$ ，上述代码只是为了绘制一个能观察训练结果能否正确划分数据集的图形而已，与上面那张图中的线性回归不一样，实际上那张图只是一个一元的线性回归模型，二元或者更高的线性模型都不能直接用二维的图形表示。

运行结果：

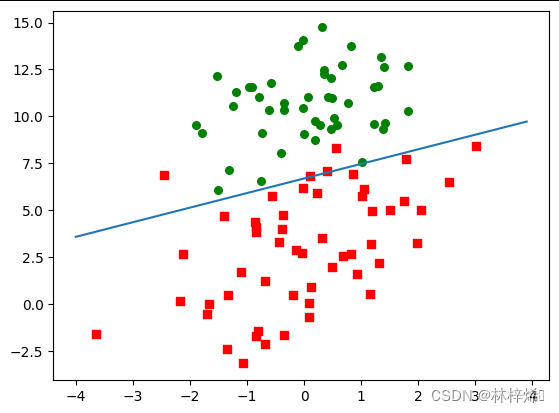
可以看到模型的分类结果是很不错的，只分类错了两个点，还有两个点卡在分界线上。

5. 训练算法：随机梯度上升

上面的梯度上升算法在每次更新回归模型参数时都需要遍历整个数据集，所需要的计算量是非常大的，在大型的数据集上上训练的话计算复杂度太高了，因此我们需要对梯度上升算法进行一些改进。一种改进方法是每次只用一个样本来更新模型参数，而不是一整个数据集一起计算，这种方法称为随机梯度上升算法，使用随机梯度上升算法进行更新参数时是选择单个的样本训练的，因此在之后增加数据集时是只使用新增的样本训练而不是像梯度上升算法一样整个数据集又重新计算一遍，因而随机梯度上升算法是一个在线学习的算法，可以不断进行增量式更新。

随机梯度上升算法的伪代码如下：

1. 将所有回归系数初始化为1

2. 对数据集中每个样本：

2.1. 计算该样本的梯度

2.2. 使用lr * grad更新模型参数

3. 返回模型参数

可以看到随机梯度上升算法与梯度上升最大的不同就是它是根据单一样本计算梯度更新参数的，而且因为是单一的样本，计算中的变量都是数值，而不是向量。

对应代码如下：

def stocGradAscent0(dataSet, classLabels):
    m, n = dataSet.shape
    lr = 0.01
    weights = torch.ones(n)
    index = 0
    for i in range(m):
        index += 1
        y_hat = torch.sigmoid((dataSet[i] * weights).sum())
        weights += lr * (classLabels[i] - y_hat) * dataSet[i]
    return weights

训练：

dataSet, classLabels = loadDataSet()
weights = stocGradAscent0(dataSet, classLabels)
print(weights)
plotPredcLine(weights, dataSet, classLabels)

训练结果：

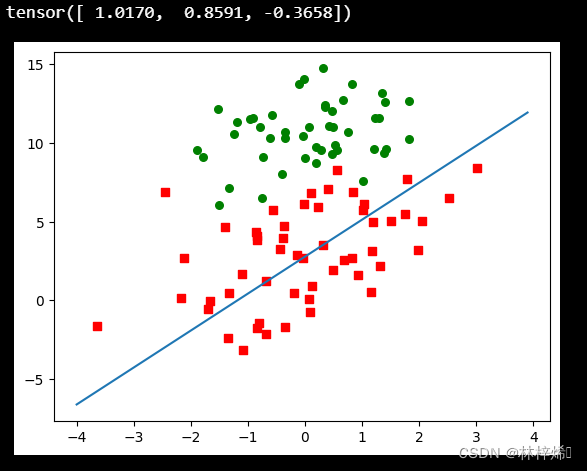
这个分类的结果就有点差了，分类错了三分之一的样本，比之前的差了很多。但是这是只迭代一次训练出的结果，而前面的梯度上升是在整个数据集上迭代了500次得到的结果，因此我们再对随机梯度上升算法改进一下，使其在整个数据集上迭代200次再观察结果。

def stocGradAscent1(dataSet, classLabels, num_epochs=200):
    m, n = dataSet.shape
    lr = 0.01
    # 保存每次更新后的模型参数
    weightList = torch.ones((num_epochs * m, n))
    weights = torch.ones(n)
    index = 0
    # 迭代num_epochs次
    for j in range(num_epochs):
        for i in range(m):
            # 每个样本都会更新一次参数，使用weightList保存模型参数
            weightList[index] = weights
            index += 1
            # 计算逻辑回归预测值y_hat
            y_hat = torch.sigmoid((dataSet[i] * weights).sum())
            # 更新模型参数
            weights += lr * (classLabels[i] - y_hat) * dataSet[i]
    # weightList是存储每次更新后的参数，每一个都是一个参数向量，
    # 而绘制图形时是绘制每个权重随迭代次数的变换，因此需要将其转置
    return weights, weightList.T

训练并绘制图形：

weights, wList = stocGradAscent1(dataSet, classLabels)
print(weights)
# print(wList)
plotPredcLine(weights, dataSet, classLabels)
plt.figure(figsize=(12, 5))
# 绘制三个参数（第一个是偏置）的更新曲线
plt.plot(wList[0], label='X0')
plt.plot(wList[1], label='X1')
plt.plot(wList[2], label='X2')
plt.xlabel('更新次数')
plt.ylabel('模型参数')
plt.legend(loc='lower right')

分类结果：

参数更新：

上面的图形乍一看上去似乎直线很平滑，但这是因为y轴的跨度范围太大了，小幅度的变化不太好直观的看出来，我们可以单独绘制三条曲线观察。

X0（偏置）：

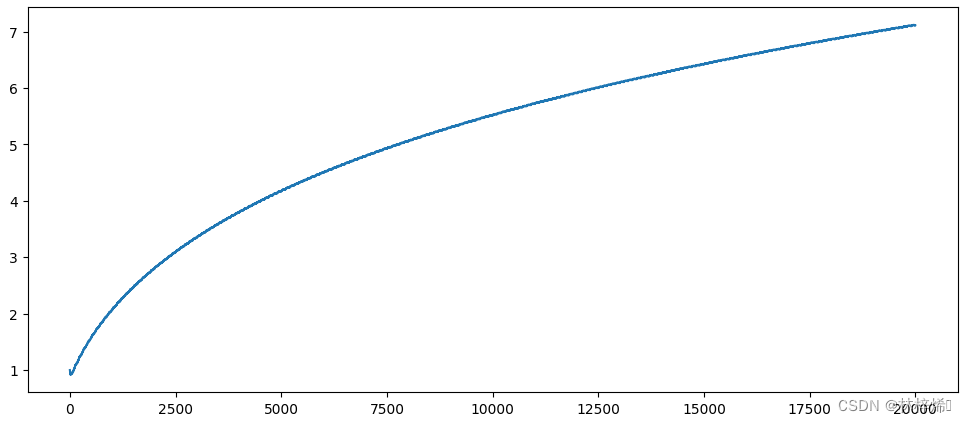
偏置变化的幅度很大，跨度从1到7，小范围内振荡比较小，可能是因为跨度过大，小范围的振荡也看不出来。

X1：

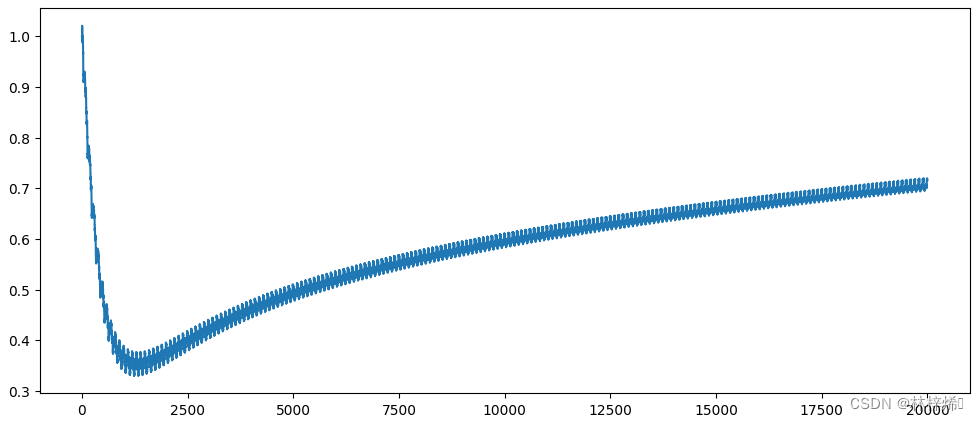
X2：

X1和X2的振荡幅度看起来就比较大了，我们可以看出二者的振荡都是周期性的，产生这种现象的原因是存在一些不能正确分类的样本点，在上面分类结果图中我们也能看出有些点是很难正确划分的，可能是噪声点。这些样本点在每次迭代时都会引发参数的剧烈改变，这样时很难收敛到一个最佳的值的，我们希望算法能避免这种周期性波动，从而收敛到某个值，因此我们需要对随机梯度算法进行一些改进。

6. 改进的随机梯度算法

针对上述问题的改进方法有：在每次迭代时调整学习率，使学习率随迭代次数不断减小，但不能减小到0，保证后续的数据对模型参数的更新也有一定的影响，这个改进可以缓解上图中的高频波动；随机抽取样本来更新参数，这种方法可以减少周期性的波动。

对应代码：

def stocGradAscent2(dataSet, classLabels, num_epochs=150):
    m, n = dataSet.shape
    weights = torch.ones(n)
    # 迭代
    for j in range(num_epochs):
        # 样本索引列表
        dataIndex = list(range(m))
        for i in range(m):
            # 调整学习率
            lr = 4 / (1. + j +i) + 0.01
            # 随机抽取一个样本（使用random函数输出一个随机值）
            randIndex = int(random.uniform(0, len(dataIndex)))
            y_hat = sigmoid((dataSet[randIndex] * weights).sum())
            weights += lr * (classLabels[randIndex] - y_hat) * dataSet[randIndex]
            # 使用完该样本后需要将该样本的索引dataIndex删除，防止下次再次访问到该样本
            del dataIndex[randIndex]
    return weights

训练：

weights, wlist = stocGradAscent2(dataSet, classLabels)
plotPredcLine(weights, dataSet, classLabels)

plt.figure(figsize=(12, 5))
plt.plot(wlist[0])

plt.figure(figsize=(12, 5))
plt.plot(wlist[1])

plt.figure(figsize=(12, 5))
plt.plot(wlist[2])

分类结果：

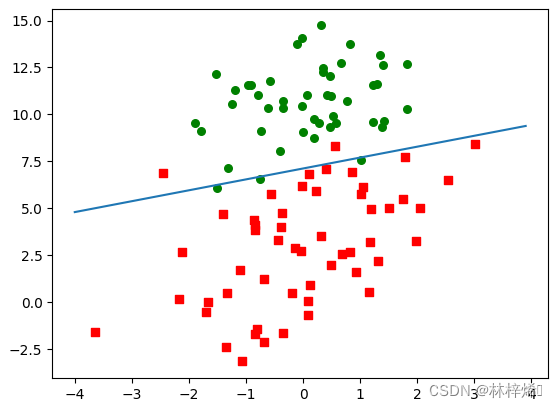
分类的结果和之前差不多，分类错了两个到五个的样本，因为这个数据集比较小，而且之前的分类结果也足够好了，所以这个改进从分类结果上看差别并不大。

X0变化：

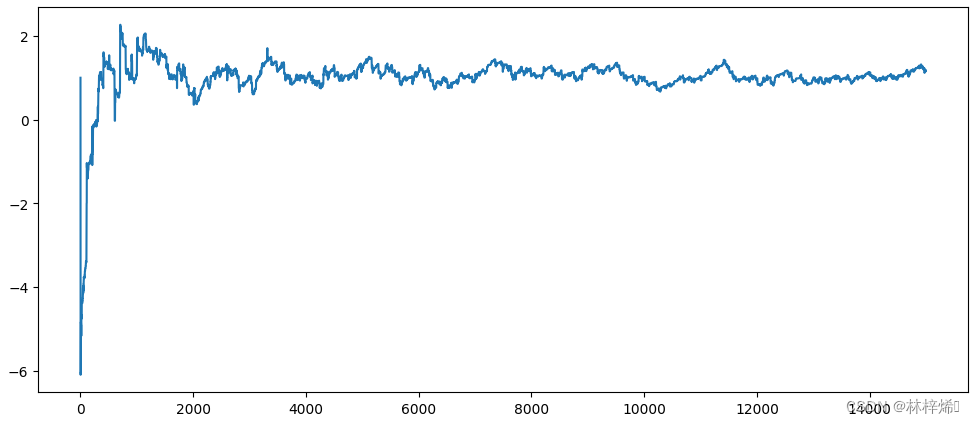
X1变化：

X2变化：

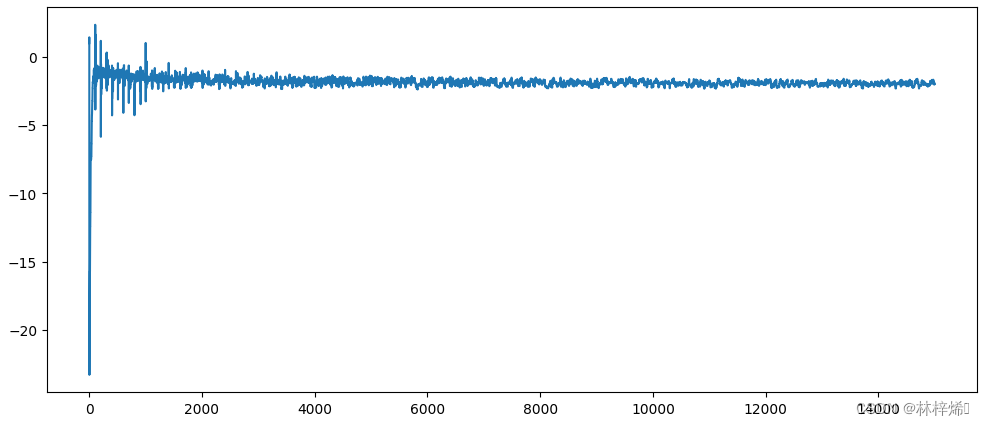
三个参数的变化就很大了，相比之前的周期性和比较剧烈的波动，这次变化的幅度还是比较小的，而且相比之前没有了周期性的波动，因此改进的算法收敛的速度更快，在第20个迭代周期的时候就已经收敛到了一个值（上图中的横坐标是更新的次数，不是迭代次数，每次迭代时要更新n（样本个数）次，也就是100次，2000实际上是第20轮迭代）。

四、从疝气病症预测病马的死亡率

我们已经掌握了逻辑回归分类的基本概念和实现流程，还学习了三种优化算法，现在我们尝试对更复杂度的数据集进行分类任务，观察我们的分类器的预测性能如何。

本节使用的数据集是Horse Colic，使用逻辑回归预测患有疝病的马的存活问题，数据集可以去UCI官网下载，下载网址为 Horse Colic – UCI Machine Learning Repository 。

1. 处理 缺失值

这次使用的数据集是包含很多缺失值的，数据中的缺失值是个非常棘手的问题，有时候数据是非常昂贵的，直接舍弃包含缺失值的整个数据是很浪费的，重新获取也是不可取的。对于缺失值，我们必须采用一些方法来解决。

一些可选的做法有：

1. 使用可用特征的均值来填补缺失值；

2. 使用特殊值来填补缺失值，如-1；

3. 忽略有缺失值的样本；

4. 使用相似样本的均值填补缺失值；

5. 使用另外的机器学习算法预测缺失值；

为了简化问题，我们直接使用特殊值0来替换所有的缺失值，因为在logistic回归中，样本的某个特征值如果为0，那么更新时就不会对该特征更新。

2. 使用logistic回归分类

读取数据集：

def readHorseDataSet(trainFileName, testFileName):
    fpTrain = open(trainFileName)
    fpTest = open(testFileName)
    trainSet = [] ; trainLabels = []
    testSet = [] ; testLabels = []
    for line in fpTrain.readlines():
        lineSplit = line.replace('?', '0').strip().split('t')
        trainSet.append(list(map(float, lineSplit[: -1])))
        trainLabels.append(float(lineSplit[-1]))
    for line in fpTest.readlines():
        lineSplit = line.replace('?', '0').strip().split('t')
        testSet.append(list(map(float, lineSplit[: -1])))
        testLabels.append(float(lineSplit[-1]))
    return torch.tensor(trainSet), torch.tensor(trainLabels).reshape((-1, 1)), torch.tensor(testSet), torch.tensor(testLabels)

分类如上面所说将概率大于0.5的样本分类为正例，将下与0.5的分类为负例，测试代码和之前一样从测试集中取样本一个个预测判断是否预测错误，统计错误个数计算错误率。

分类和预测：

def classify2(inX, weights):
    # 计算预测值
    prob = torch.sigmoid((inX * weights).sum())
    # 预测值大于0.5的分类为1，小于的分类为0
    if prob > 0.5:
        return 1
    else:
        return 0

def colicTest(trainSet, trainLabels, testSet, testLabels):
    trainWeights, wlist = stocGradAscent2(trainSet, trainLabels, 500)
    errCount = 0
    for i in range(len(testSet)):
        sample = testSet[i]
        if int(classify2(sample, trainWeights)) != int(testLabels[i]):
            errCount += 1
    errRate = errCount / len(testSet)
    return errRate

进行训练和预测：

trainSet, trainLabels, testSet, testLabels = readHorseDataSet('horseColicTraining.csv', 'horseColicTest.csv')
errRate = colicTest(trainSet, trainLabels, testSet, testLabels)
print(errRate)