IBM Qiskit量子机器学习速成（二）

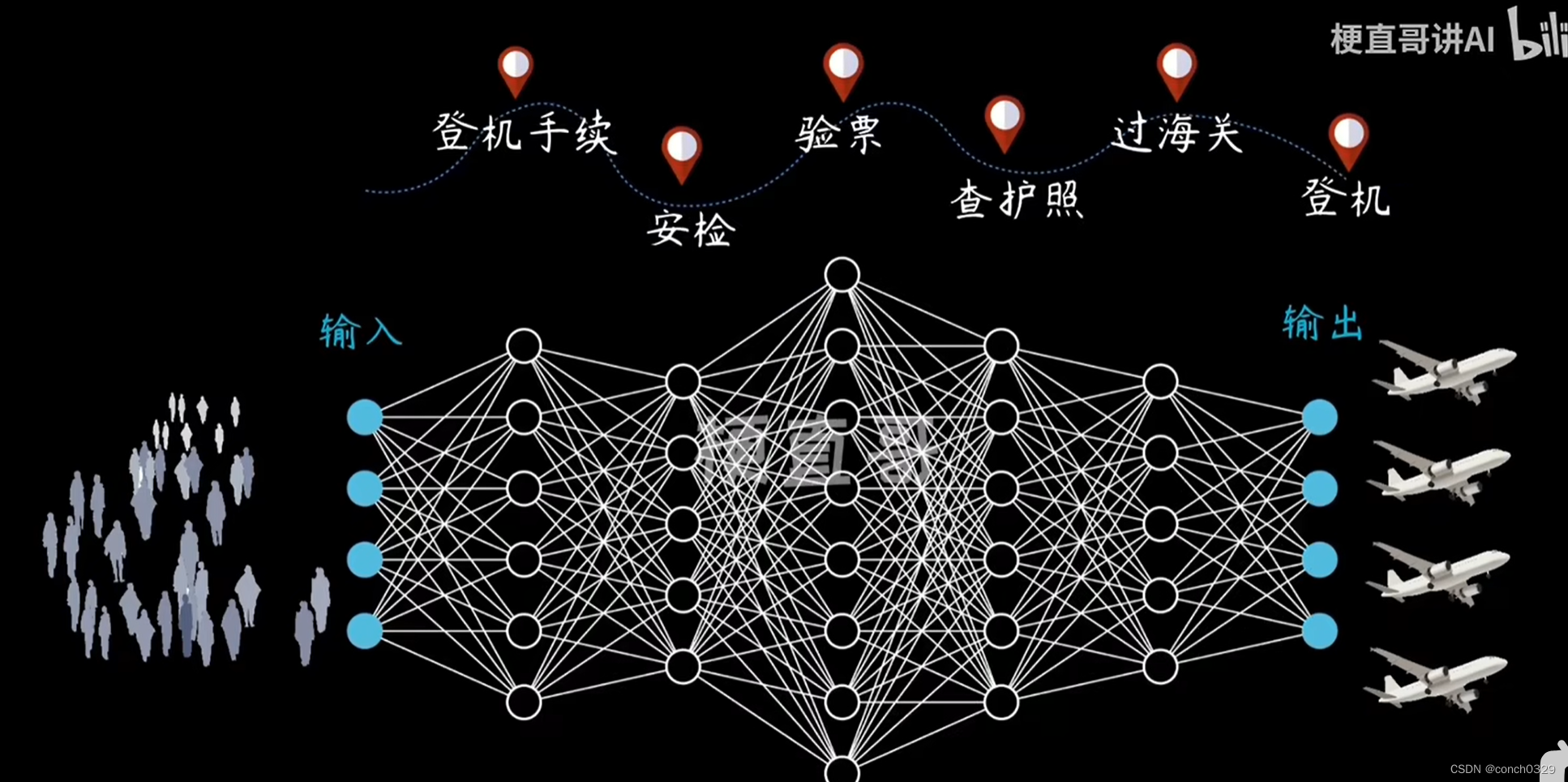
分类与回归

本章节介绍如何使用量子神经网络处理机器学习中的分类与回归任务。一般而言，我们将这两大内容归类为“监督学习(supervised learning)”

一般流程

使用量子神经网络处理分类与回归任务的一般步骤如下：

1. 创建参数化电路，参数可以是Parameter（单参数）、由Parameter组成的列表或ParameterVector（多参数）
2. 将参数化电路传入量子神经网络（EstimatorQNN或者SamplerQNN，前者一般用于期望值估计，后者一般关注某一特殊状态的概率），一般格式为

xxxQNN(
    circuit=qc,  # 你的参数化电路
    input_params=params1, # 你的输入参数，即你准备的数据
    weight_params=params2, # 你的权重参数，即机器学习模型本身的参数
)

• 需要从qiskit_machine_learning.neural_networks库中导入神经网络

3. 创建分类器或回归器

• 需要从qiskit_machine_learning.algorithms.classifiers库中导入NeuralNetworkClassifier
• 需要从qiskit_machine_learning.algorithms.regressors库中导入NeuralNetworkRegressor

# 分类器
c1 = NeuralNetworkClassifier(
    neural_network=qnn, # 你准备的量子神经网络
    optimizer=optimizer # 误差函数或优化器
)

# 回归器
r1 = NeuralNetworkRegressor(
    neural_network=qnn, # 你准备的量子神经网络
    optimizer=optimizer # 误差函数或优化器
)

4. 分类器或回归器的使用

c1.fit(train_X, train_y)  # 使用训练数据拟合分类器
c1.predict(test_X)  # 预测测试数据的结果
c1.score(test_X, test_y)  # 计算得分以评判模型优劣（神经网络和误差函数是否选择得当）

r1.fit(train_X, train_y)  # 使用训练数据拟合回归器
r1.predict(test_X)
r1.score(test_X, test_y)

5. 使用Qiskit提供的VQC或VQR类简化上述步骤

• 需要从qiskit_machine_learning.algorithms.classifiers库中导入VQC
• 需要从qiskit_machine_learning.algorithms.regressors库中导入VQR

vqc = VQC(
    feature_map=feature_map,  # 数据编码电路
    ansatz=ansatz,  # 模型参数所在电路/神经网络的层所在电路
    optimizer=optimizer,  # 优化器
)

vqr = VQR(
    feature_map=feature_map,  # 数据编码电路
    ansatz=ansatz,  # 模型参数所在电路/神经网络的层所在电路
    optimizer=optimizer,  # 优化器
)

其中出现的feature_map、ansatz等词的含义下文会讲。

实战演练

回归问题

温馨提醒：以下代码段应合并为一整个代码文件

首先导入本次需要的所有库文件

import numpy as np
from qiskit import QuantumCircuit       # 量子电路
from qiskit.circuit import Parameter        # 参数
from qiskit_algorithms.optimizers import L_BFGS_B  # 优化器的一种，你可以选择其他优化器
from qiskit_machine_learning.algorithms.regressors import NeuralNetworkRegressor, VQR
from qiskit_machine_learning.neural_networks import EstimatorQNN
from qiskit_machine_learning.circuit.library import QNNCircuit

接下来我们先“故意”编造我们的数据

num_samples = 20
eps = 0.01
lb, ub = -np.pi, np.pi
X_ = np.linspace(lb, ub, num=50).reshape(50, 1)
f = lambda x: np.sin(x)

X = (ub - lb) * np.random.random([num_samples, 1]) + lb
y = f(X[:, 0]) + eps * (2 * np.random.random(num_samples) - 1)

num_samples是我们的样本点个数或说样本容量，eps是误差。我们首先在

[

−

π

,

π

]

[-pi, pi]

[−π,π]区间上均匀地获得了若干自变量值，随后随机地在这个区间上采样得到X，代入函数值并加上噪声得到y。如果不加噪声，y会是一个X的精确函数，既不现实，也不没有执行回归算法的意义。

下一步，我们要创建量子神经网络

param_x = Parameter("x")
feature_map = QuantumCircuit(1, name="fm")
feature_map.ry(param_x, 0)

# construct simple ansatz
param_y = Parameter("y")
ansatz = QuantumCircuit(1, name="vf")
ansatz.ry(param_y, 0)

# construct a circuit
qc = QNNCircuit(feature_map=feature_map, ansatz=ansatz)

regression_estimator_qnn = EstimatorQNN(
    circuit=qc
)

feature_map意为特征映射，意味着我们需要把经典数据代表的数据特征映射成量子比特。ansatz本意为“假设”，在量子机器学习中表示我们“对机器学习模型结构的初始猜测”，这一模型的参数后续可以得到优化（就像高中数学中的二分法求根，需要先指定一个点才能开始迭代）。

随后，我们就可以创建变分量子回归器(Variational Quantum Regressor, VQR)了。我们这里先用最繁难的方法处理一遍（即使用NeuralNetworkRegressor）。

regressor = NeuralNetworkRegressor(
    neural_network=regression_estimator_qnn,
    loss="squared_error",
    optimizer=L_BFGS_B(maxiter=5),
)

我们这里先是传入了自定义的神经网络，又传入了一个指定的损失函数L_BFGS_B，并且规定最大迭代次数为5。

最后，我们直接代入数据进行拟合

regressor.fit(X, y)

print(regressor.score(X, y))

如果想简化上述过程，我们可以使用VQR

vqr = VQR(
    feature_map=feature_map,
    ansatz=ansatz,
    optimizer=L_BFGS_B(maxiter=5),
    callback=callback_graph,
)
vqc.fit(X, y)

print(vqc.score(X, y))

部分聪明的读者会想尝试拟合直线，但是得到了极其离谱的得分。原因在于Qiskit官网的这一例子能给出的期望值被限制在

[

−

1

,

1

]

[-1,1]

[−1,1]之间。

分类问题

本次用到的库如下

from sklearn.datasets import load_iris
from sklearn.preprocessing import MinMaxScaler
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
from qiskit.circuit.library import ZZFeatureMap, RealAmplitudes
from qiskit_algorithms.optimizers import COBYLA
from qiskit.primitives import Sampler
from qiskit_machine_learning.algorithms import VQC

由于我们要使用真实数据（知名的鸢尾花数据），所以导入了sklearn库。我们通过如下方式使用这一数据

iris_data = load_iris()  # 加载数据
features = iris_data.data  # 特征即数据
labels = iris_data.target  # 标签即目标

你可以尝试打印这两个变量，观察数据的形状。其中记录了鸢尾花花萼与花瓣的大小，我们知道这两个数据的范围是不同的（如果高中主科和副科的考试总分不同），这对我们的训练不利，我们需要将其标准化到

[

0

,

1

]

[0,1]

[0,1]区间上。

features = MinMaxScaler().fit_transform(features)  # 标准化数据/特征

下一步，我们将总数据分割成训练集与测试集（就像人类学习知识时，先做习题，再考试）。

train_features, test_features, train_labels, test_labels = train_test_split(
    features, labels, train_size=0.8
)

制备好数据集后，我们可以正式进入到量子机器学习的分类方法了。首先我们使用ZZFeatureMap将我们鸢尾花的花萼与花瓣两类数据编码为量子比特。

num_features = features.shape[1]  # 特征数

# 特征数与数据集保持一致，reps的数量会决定量子门序列的重复次数，影响保真率
feature_map = ZZFeatureMap(num_features, reps=1)

注意！我们只是准备了导入接口，还没有导入数据！

随后，使用RealAmplitudes作为神经网络的层（即可调参数的一种模型）。

ansatz = RealAmplitudes(num_qubits=num_features, reps=4)

最后，我们创建量子分类器

vqc = VQC(
    num_features,
    feature_map,
    ansatz,
    optimizer=COBYLA(maxiter=100)
)

拟合数据并打印结果

vqc1.fit(train_features, train_labels)
print(vqc1.score(train_features, train_labels))
print(vqc1.score(test_features, test_labels))

代码007普通

打赏 收藏 海报 链接