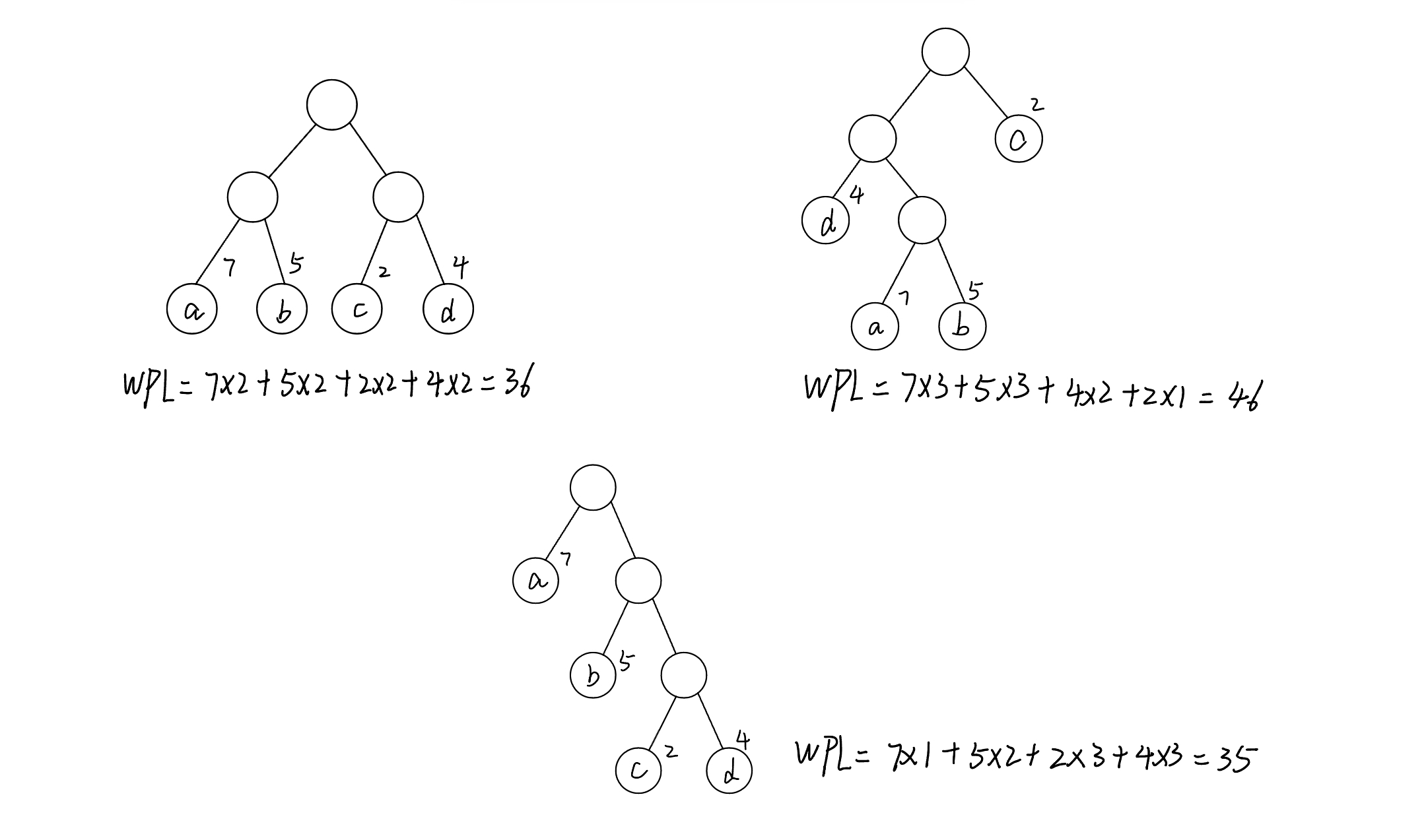
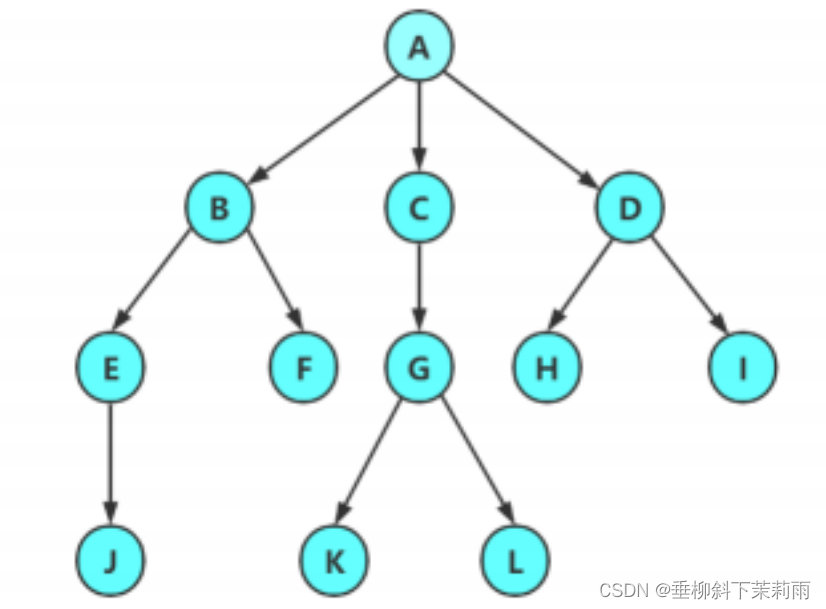
算法分析复习重点

try(int t)
{
    int j;

    // 如果当前处理的位置 t 超过了总数 n，说明已经生成了一种排列，输出结果
    if (t &gt; n)
    {
        output();
    }
    else
    {
        // 遍历当前位置 t 到 n 的所有可能的值
        for (j = t; j <= n; j++)
        {
            // 将当前位置 t 的元素与位置 j 的元素交换
            swap(t, j);

            // 递归调用 try 函数，处理下一个位置 t+1
            try(t + 1);

            // 回溯时，恢复原来的排列，将之前交换的元素还原
            swap(t, j);
        }
    }
}

try(1):
  for j = 1 to 3:
    swap(1, 1)  # 选择了数字1放在第一个位置
    try(2):
      for j = 2 to 3:
        swap(2, 2)  # 选择了数字2放在第二个位置
        try(3):
          for j = 3 to 3:
            swap(3, 3)  # 选择了数字3放在第三个位置
            try(4):
              t &gt; n，输出排列 [1, 2, 3]
            回溯，执行 swap(3, 3) 恢复原来的排列 [1, 2, 3]
        回溯，执行 swap(2, 2) 恢复原来的排列 [1, 2, 3]
      for j = 3 to 3:
        swap(2, 3)  # 选择了数字3放在第二个位置
        try(3):
          ...
        回溯，执行 swap(2, 3) 恢复原来的排列 [1, 2, 3]
    回溯，执行 swap(1, 1) 恢复原来的排列 [1, 2, 3]
  for j = 2 to 3:
    swap(1, 2)  # 选择了数字2放在第一个位置
    try(2):
      ...
    回溯，执行 swap(1, 2) 恢复原来的排列 [1, 2, 3]
  for j = 3 to 3:
    swap(1, 3)  # 选择了数字3放在第一个位置
    try(2):
      ...
    回溯，执行 swap(1, 3) 恢复原来的排列 [1, 2, 3]

当 t=1，n=3 时，整个过程如下：

try(1):
- 第一次循环，j 的初始值是1。
  - 执行 swap(1, 1)，选择了数字1放在第一个位置。
  - 递归调用 try(2)。
try(2):
- 第一次循环，j 的初始值是2。
  - 执行 swap(2, 2)，选择了数字2放在第二个位置。
  - 递归调用 try(3)。
try(3):
- 第一次循环，j 的初始值是3。
  - 执行 swap(3, 3)，选择了数字3放在第三个位置。
  - 递归调用 try(4)。
try(4):
- 在这里，t > n，输出当前排列 [1, 2, 3]。
- 回溯，执行 swap(3, 3) 恢复原来的排列 [1, 2, 3]。
回到 try(3):
- 第二次循环，j 的初始值是3。
  - 执行 swap(3, 3)，选择了数字3放在第三个位置。
  - 递归调用 try(4)。
try(4) （第二次调用）:
- 在这里，t > n，输出当前排列 [1, 2, 3]。
- 回溯，执行 swap(3, 3) 恢复原来的排列 [1, 2, 3]。
回到 try(2):
- 第二次循环，j 的初始值是2。
  - 执行 swap(2, 2)，选择了数字2放在第二个位置。
  - 递归调用 try(3)。
try(3) （第二次调用）:
- 第一次循环，j 的初始值是3。
  - 执行 swap(3, 3)，选择了数字3放在第三个位置。
  - 递归调用 try(4)。
try(4) （第三次调用）:
- 在这里，t > n，输出当前排列 [1, 3, 2]。
- 回溯，执行 swap(3, 3) 恢复原来的排列 [1, 2, 3]。
回到 try(3) （第二次调用）:
- 第二次循环，j 的初始值是3。
  - 执行 swap(3, 3)，选择了数字3放在第三个位置。
  - 递归调用 try(4)。
try(4) （第四次调用）:
- 在这里，t > n，输出当前排列 [1, 3, 2]。
- 回溯，执行 swap(3, 3) 恢复原来的排列 [1, 2, 3]。
回到 try(2):
- 第三次循环，j 的初始值是3。
  - 执行 swap(2, 3)，选择了数字3放在第二个位置。
  - 递归调用 try(3)。
try(3) （第三次调用）:
- 第一次循环，j 的初始值是3。
  - 执行 swap(3, 3)，选择了数字3放在第三个位置。
  - 递归调用 try(4)。
try(4) （第五次调用）:
- 在这里，t > n，输出当前排列 [2, 1, 3]。
- 回溯，执行 swap(3, 3) 恢复原来的排列 [1, 2, 3]。
回到 try(3) （第三次调用）:
- 第二次循环，j 的初始值是3。
  - 执行 swap(3, 3)，选择了数字3放在第三个位置。
  - 递归调用 try(4)。
try(4) （第六次调用）:
- 在这里，t > n，输出当前排列 [2, 1, 3]。
- 回溯，执行 swap(3, 3) 恢复原来的排列 [1, 2, 3]。
回到 try(2):
- 第四次循环，j 的初始值是3。
  - 执行 swap(2, 3)，选择了数字3放在第二个位置。
  - 递归调用 try(3)。
try(3) （第四次调用）:
- 第一次循环，j 的初始值是3。
  - 执行 swap(3, 3)，选择了数字3放在第三个位置。
  - 递归调用 try(4)。
try(4) （第七次调用）:
- 在这里，t > n，输出当前排列 [2, 3, 1]。
- 回溯，执行 swap(3, 3) 恢复原来的排列 [1, 2, 3]。
回到 try(3) （第四次调用）:
- 第二次循环，j 的初始值是3。
  - 执行 swap(3, 3)，选择了数字3放在第三个位置

留学咨询

1.2024年国内考研报名已经截至，据统计今年报考人数已经突破500W人!

从往年的数据可以看出，国内考研人数逐年增加，考生竞争压力也变得越来越大，学历的价值也越来越重要。相比国内，国外的研究生学制整体来说较短一些，且入学申请政策相较于国内考研来说也更加灵活，比如国内一年-考、一考定胜负，在国外会更加丰富一些，不会一局定“输赢”。不仅如此，国外还可以同时申请多所学校和多个专业，甚至还可以选择多国联申，只要选校、选专业的策略正确，一般都可以申请到比较满意的院校和专业。考研总是存在各种变数，大家只有做好“两手准备，才能拥有双重保障”。

2.Ni ch e 发布2024年全美最难进入的大学排名！

从榜单中可以看出，上榜的美国大学，无论是综合大学还是文理学院，录取率普遍低于10%，真是当之无愧的“高冷校”，申请难度可想而知。加州理工学院、斯坦福大学、麻省理工学院一直是“精英和学霸的聚集地”，无论是科研实力、师资力量，还是国际影响力，都享有极高赞誉。正因如此，大学招生官在考察申请者时，往往更青睐优秀且富有创造力和独特性的学生。
波莫纳学院仍是全美最难录取的文理学院，斯沃斯莫尔学院、鲍登学院、科尔比学院等，录取难度丝毫不逊于顶尖综合性大学。