【算法刷题】Day12

本文介绍: 要大胆的去想状态表示和状态转移方程。

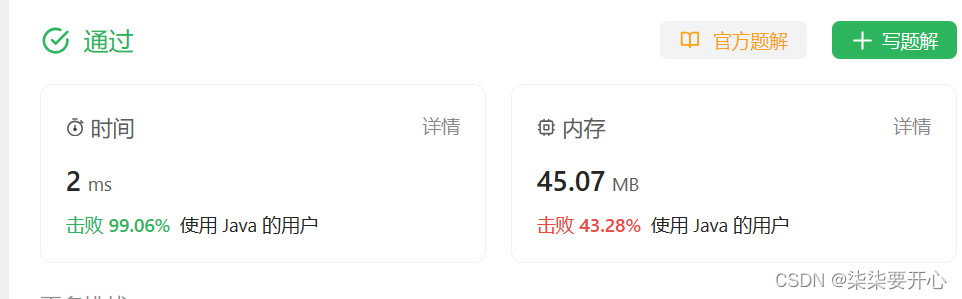
1004. 最大连续1的个数 III

在这里插入图片描述

原题链接

题干：

这是一个二进制数组，里面都是 0 和 1
最多翻转 k 个 0
返回连续 1 的最大个数

这个时候，如果真的一个一个翻转然后判断过于麻烦，我们可以通过判断一个区间内，有没有大于 k 个 0，如果有那就翻转不了，如果没有就可以顺利翻转

算法 原理：

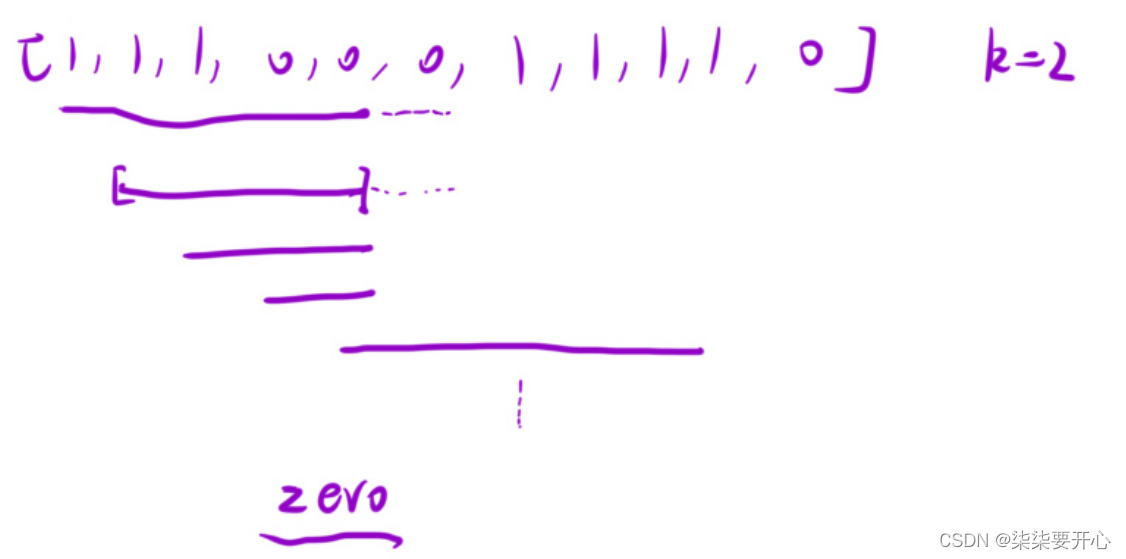
1、暴力枚举 + 计数器

这个时候，固定一个起点，然后去枚举终点
用计数器来记住里面 0 的个数（这里用的是zero）
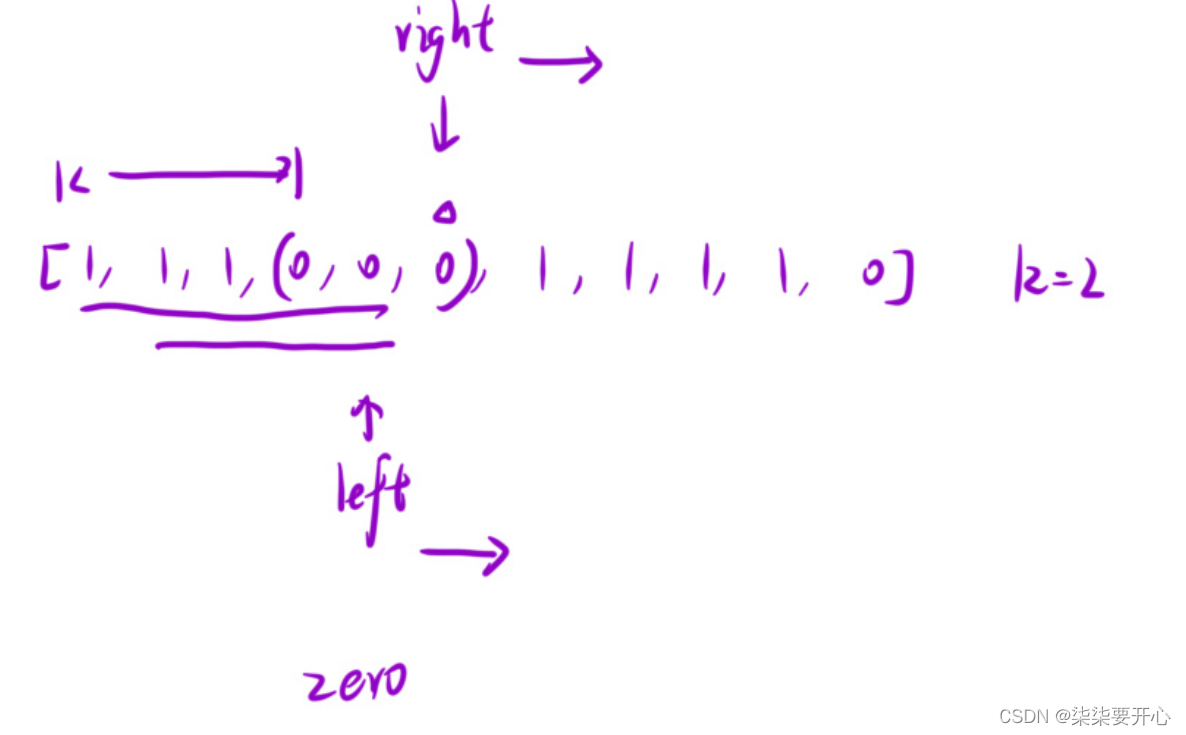
在这里插入图片描述

2、利用 滑动 窗口

由于我们在枚举的可以看到，如果 right 走到了第三个 0 的位置，那么个数超过了k，说明不是结果，如果直接 left++ 走到了第二个 1 的位置
继续遍历，已经会经过第三个 0，依然还要left ++
这样下去，都是一些重复的操作，所以我们对方法一进行优化，让left 直接走到 0 不超过 k
在这里插入图片描述

上述优化就可以用滑动窗口来写

初始化 left = 0; right = 0;
进窗口（r i g ht = 1无视，r i g ht = 0计数器++）
判断（zero &g t; k）
出窗口
更新结果

代码：

class Solution {
    public int longestOnes(int[] nums, int k) {
        
        int ret = 0;
        for (int right = 0, left = 0, zero = 0; right &lt; nums.length; right++) {
            if (nums[right] == 0) {
                zero++;
            }
            while (zero &gt; k) {
                if (nums[left++] == 0) {
                    zero--;
                }
            }
            ret = Math.max(ret,right - left + 1);
        }
        return ret;
    }
}

在这里插入图片描述

746. 使用 最小花费爬楼梯

在这里插入图片描述

原题链接

题干：

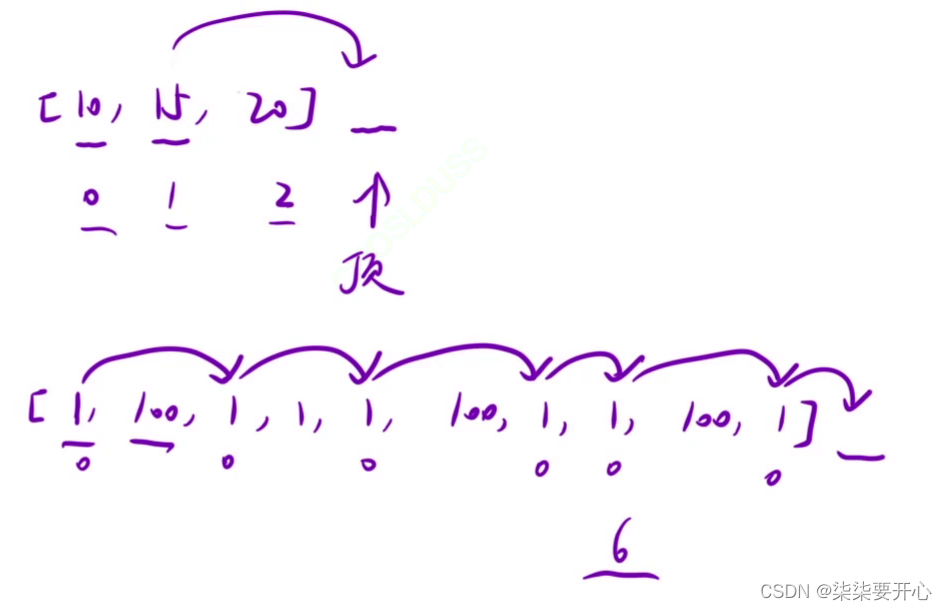
在一个整数数组中，花费 cost[i]可向上走一个或者；两个台阶
可以从 0 或者 1 下标的台阶爬楼梯

这个时候对两个示例进行画图，可以看到，这里的楼顶是数组后面的位置

在这里插入图片描述

算法 原理：

解法一：

1.1 状态 表示

经验 + 题目要求
以 i 位置为起点…
dp[i] 表示：到达 i 位置时，最小花费

1.2 状态转移方程

用之前或者之后的状态，推导出 dp[i] 的值
根据最近的一步，来划分问题

这里到达 i 位置，能从 i-1 或者 i-2 位置到达

在这里插入图片描述
这个时候，状态转移方程就可以求出来了
dp[i] = min( dp[i-1] + cost[i-1] , d p[i-2] + cost[i-2]

1.3 初始化

要保证填表的时候不越界
d p[0] = d p[1] = 0

1.4 填表顺序

从左往右

1.5 返回值

dp[n]

1.6 代码 编写

class Solution {
    public int minCostClimbingStairs(int[] cost) {
        int n = cost.length;
        int[] dp = new int[n + 1];
        for (int i = 2; i <= n; i++) {
            dp[i] = Math.min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
        }
        return dp[n];
    }
}

在这里插入图片描述

解法二：

2.1 状态表示

经验 + 要求
以 i 位置为起点…
dp[i] 表示：从 i 位置出发，到达楼顶，此时的最小花费

2.2 状态转移方程

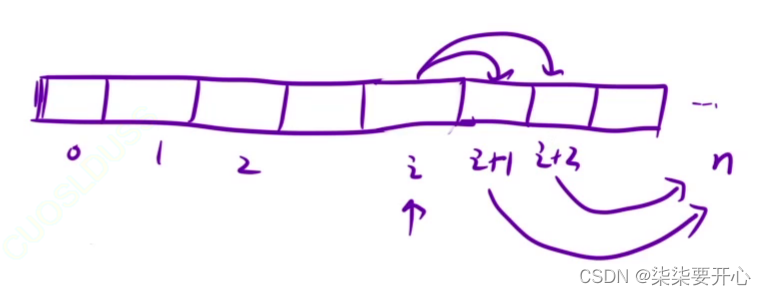
在这里插入图片描述

dp[i] = min(dp[i+1] + cost[i] , dp[i+2] + cost[i+2]

2.3 初始化

dp[n-1] = cost[n-1]
dp[n-2] = cost[n-2]

2.4 填表顺序

从右往左

2.5 返回值

min( dp[0], dp[1] )

2.6 代码 编写

class Solution {
    public int minCostClimbingStairs(int[] cost) {
        int n = cost.length;
        int[] dp = new int[n];
        dp[n - 1] = cost[n - 1];
        dp[n - 2] = cost[n - 2];
        for (int i = n - 3; i >= 0; i--) {
            dp[i] = Math.min(dp[i + 1] , dp[i + 2]) + cost[i];
        }
        return Math.min(dp[0],dp[1]);
    }
}