数据结构算法-选择排序算法

本文介绍: 当然，选择排序只是一种基础的排序算法，对于更复杂的排序任务，需要使用更加高效的排序算法，以提高排序的速度和效率。只要排序外层循环 i=（ 0~ n-1 ） (n&g t;0) 定义 max index 最大索引默认为0 内层循环j 1到 n-i 比较次数。如果这个找到的max的值不等于当前末尾的值也就是 n-i-1；可能关键字的不同对应的是不同的视频搜索，排序是算法必备的。

引言

说起排序算法，那可就多了去，首先了解什么叫排序
以B站为例：
在这里插入图片描述
蔡徐坤在B站很受欢迎呀，先来看一下综合排序就是播放量和弹幕量，收藏量一键三连都很高这是通过一些排序算法才能体现出综合排序

在这里插入图片描述
蔡徐坤鬼畜按照播放量来看最高的进行排序，当然也可以按照搜索的结果来进行排序
关键字对于搜索的结果而言非常重要提供关键字找到对应的视频在根据关键字对应的视频排序

可能关键字的不同对应的是不同的视频搜索，排序是算法必备的
同时，还可以考虑用户的个性化推荐，根据用户的观看历史、搜索历史、点赞评论等行为数据，利用机器学习算法进行推荐。这样可以更精准地推荐用户感兴趣的蔡徐坤鬼畜视频，并提高用户的满意度和留存率。

所以排序有非常多种，此时想必疑惑，“这和选择排序有什么关系呢？” 当然有关系。
选择排序是一种简单的排序算法，可以应用到蔡徐坤鬼畜视频排序中。例如，可以根据视频的播放量或者点赞数进行选择排序，按照从大到小的顺序排列视频，从而让用户更容易找到热门的、受欢迎的蔡徐坤鬼畜视频。当然，选择排序只是一种基础的排序算法，对于更复杂的排序任务，需要使用更加高效的排序算法，以提高排序的速度和效率。

选择排序思路

在这里插入图片描述
一共是7个数据元素，
只要排序外层循环 i=（ 0~ n-1 ） (n&g t;0) 定义 max index 最大索引默认为0 内层循环j 1到 n-i 比较次数
n-i ：当前还有多少未排序的元素
n-i-1：当前已排序序列的最后一个元素的索引

第一次外层循环
 i=0
max=0
第一次内层循环
j=1 j<7-i;
如果 115&g t; 165
j++
直到 j=5 更新 max index=j
max此时=5
内层循环遍历结束
如果这个找到的m a x的值不等于当前末尾的值也就是 n-i-1；交换数组对应的位置交换后
第一次外层循环结束

外层循环开始。i代表当前已排序序列的长度（因为每次排序后，i会+1）。外层循环从0开始，到size – 2结束，共进行size – 1次循环。
初始化最大值的索引为0，因为假设第一个元素是当前未排序元素中的最大值。
内层循环开始。j代表当前未排序序列的长度。内层循环从0开始，到size – i – 1结束，每次循环中都寻找未排序序列中的最大值。
如果当前元素大于当前认为的最大值，那么更新最大值的索引。
内层循环结束后，我们得到了未排序元素中的最大值的位置。
如果最大值的索引不等于（size – i – 1），说明最大值不在正确的位置上，需要交换。
交换最大值和最后一个已排序元素的位置。
重复上述步骤，直到所有元素都已排序。

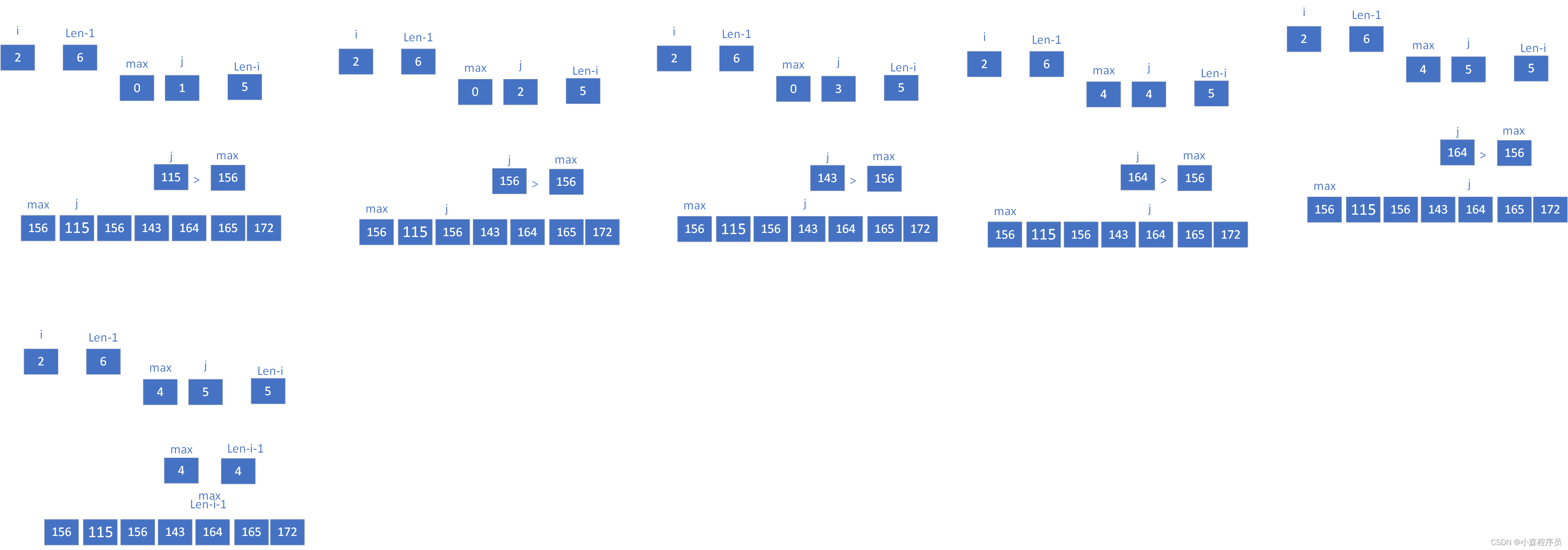
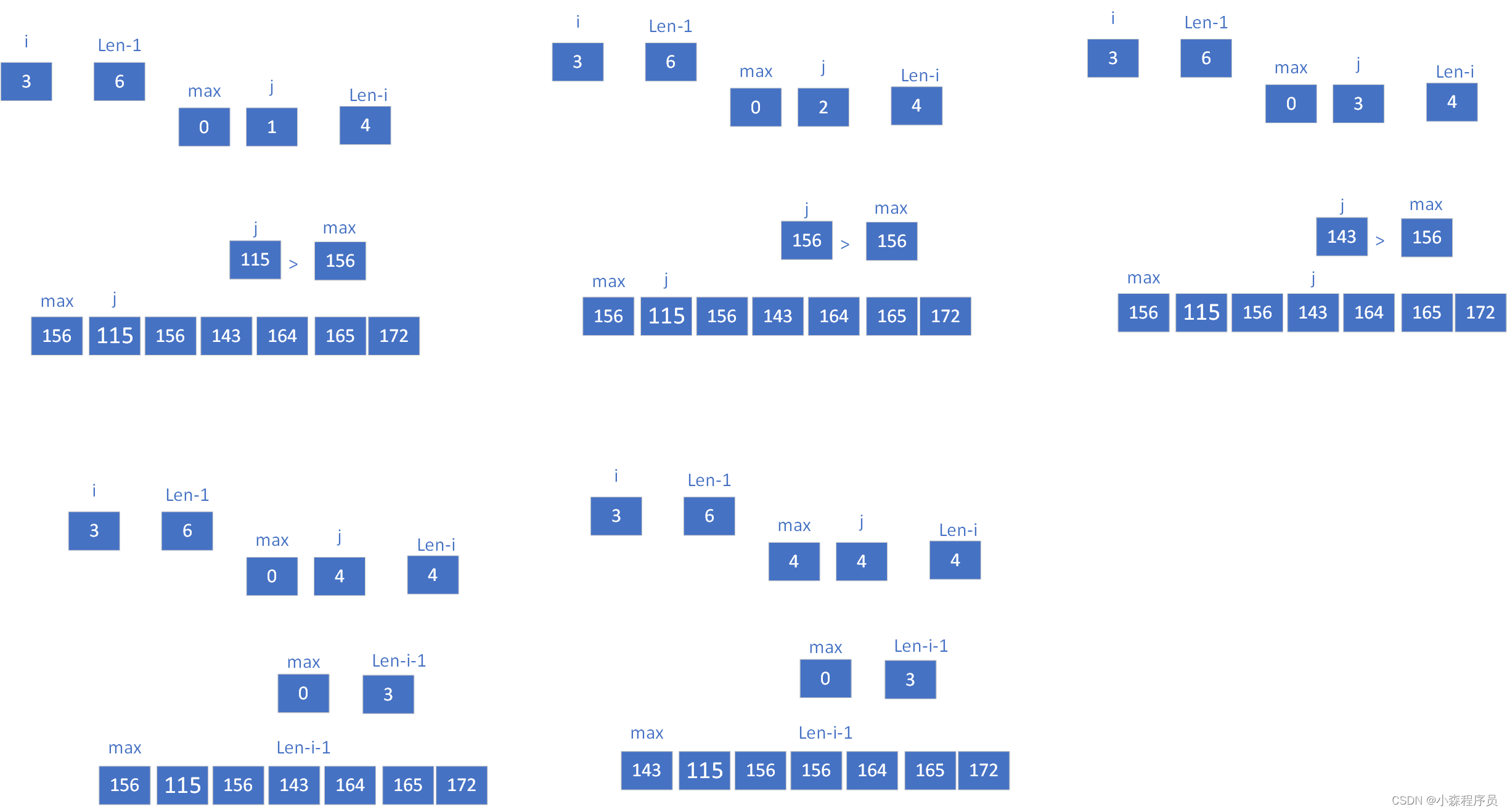
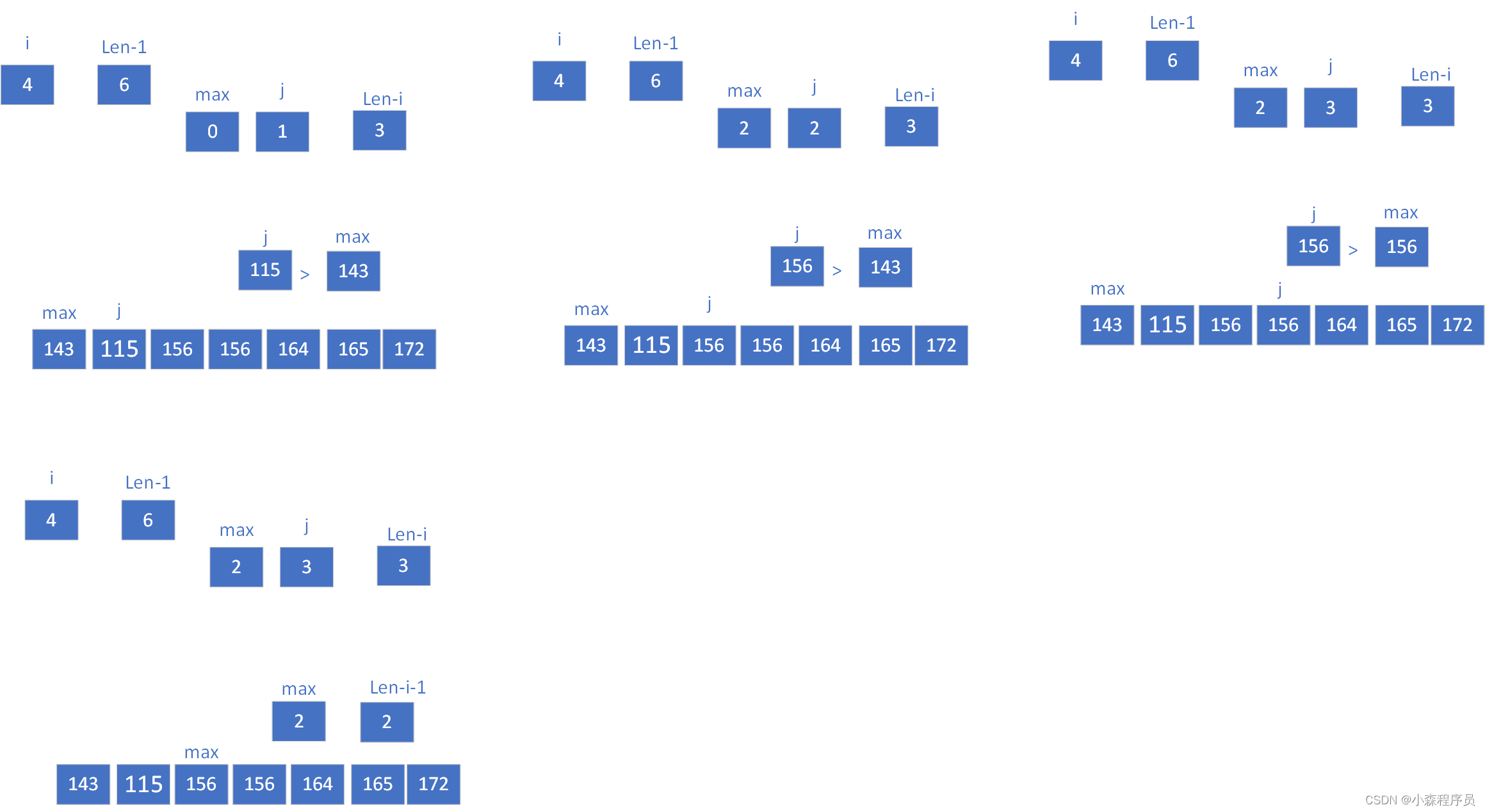
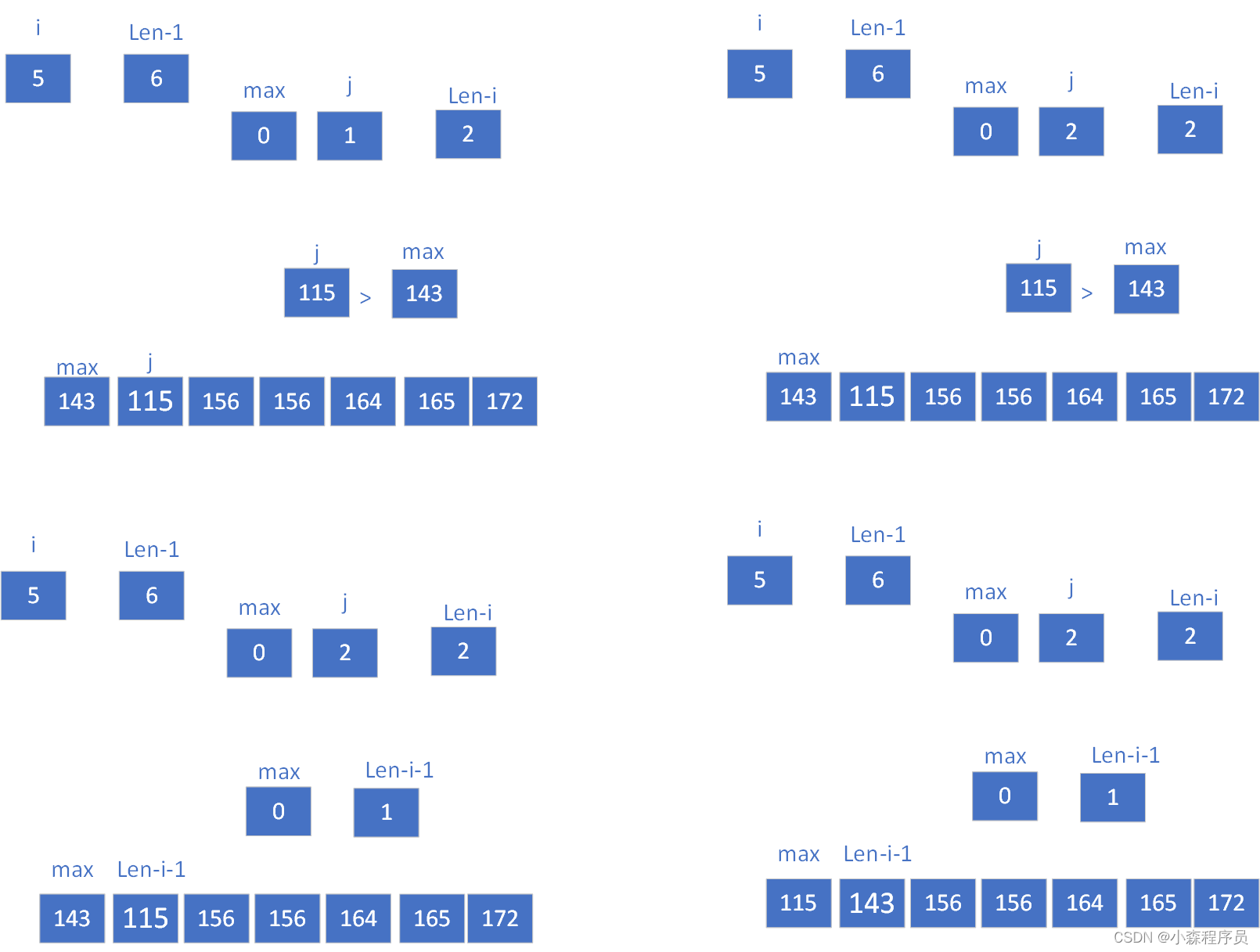
在这里插入图片描述

这是每次排序的结果
在这里插入图片描述

选择排序算法专区

// 定义一个函数 SelectSort，它接受一个整数数组 arr，数组的大小 size，和一个比较函数 cmp 作为参数  
void SelectSort(int arr[], int size,bool(*cmp)(const int &amp;,const int &amp;)) {  
  
    // 如果传入的比较函数是空指针，直接返回，不做任何操作  
    if (cmp == nullptr) {  
        return;  
    }  
  
    // 开始循环，从数组的第一个元素到倒数第二个元素（i 从 0 到 size-2）  
    for (int i = 0; i < size-1; i++){  
  
        // 初始化最大或最小元素的索引为 0  
        int MaxorMinindex = 0;  
  
        // 从数组的第二个元素开始，到倒数第三个元素（j 从 1 到 size-i-1）  
        for (int j = 1; j < size-i; j++){  
  
            // 使用比较函数 cmp 来判断 arr[j] 是否大于或小于 arr[MaxorMinindex]，如果小于或等于，更新 MaxorMinindex 为 j  
            if (cmp(arr[j],arr[MaxorMinindex])) {  
                MaxorMinindex = j;  
            }  
        }  
  
        // 如果 MaxorMinindex 不等于 size - i - 1（也就是当前未排序部分最后一个元素的索引），交换 arr[MaxorMinindex] 和 arr[size - i - 1] 的值  
        if (MaxorMinindex != size - i - 1) {  
            swap(arr[MaxorMinindex], arr[size - i - 1]);  
        }  
    }  
}  
  
// 定义一个函数 lessCmp，接受两个整数作为参数，如果第一个整数小于第二个整数，返回 true，否则返回 false  
bool lessCmp(const int&amp; val1, const int &amp;val2) {  
    return val1 < val2;  
}  
  
// 定义一个函数 GreaterCmp，接受两个整数作为参数，如果第一个整数大于第二个整数，返回 true，否则返回 false  
bool bool GreaterCmp(const int&amp; val1, const int &amp;val2) {

	return val1 &gt; val2;
}