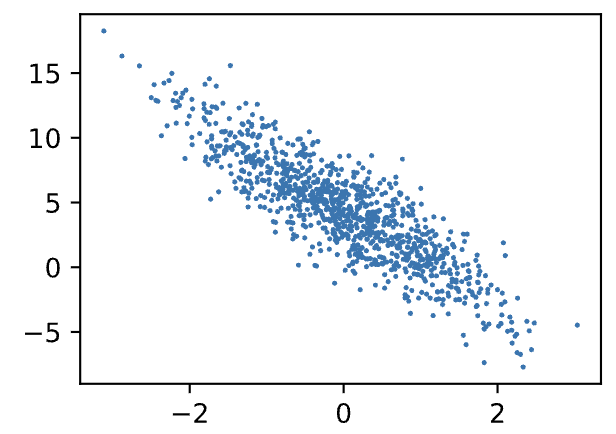
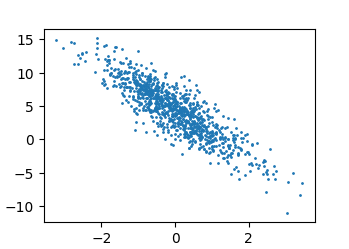
本文介绍: 这种损失的问题是,有时误差可能会在单个样本之间抵消,导致零损失,这可能会产生误导。这种损失在行为上非常接近Huber损失,因为它对于非常大的误差值具有线性行为,而对于小的损失值具有二次性行为。这里的好处是,您不必像Huber损失的情况那样决定阈值的值。损失函数与标度无关,因为它是两个对数值的差,这与值的比值的对数相同。接近零的值,其中零是最佳值,是一个好模型的特征。对于超过阈值的损失值,损失是线性的,否则是二次的。损失函数与标度无关,因为它是两个对数值的差,这与值的比值的对数相同。
12. HUber损失
L
δ
=
{
13. 对数余弦损失
14. 分位数损失函数
15. 后验极大似然损失函数
16. 泊松损失
声明:本站所有文章,如无特殊说明或标注,均为本站原创发布。任何个人或组织,在未征得本站同意时,禁止复制、盗用、采集、发布本站内容到任何网站、书籍等各类媒体平台。如若本站内容侵犯了原著者的合法权益,可联系我们进行处理。